一、实验原理
频率域滤波是对图像进行傅里叶变换,将图像由图像空间转换到频域空间,然后在频率域中对图像的频谱作分析处理,以改变图像的频率特征,原理是用傅里叶变换表示的函数特征完全可以通过傅里叶反变换来重建,而且不会丢失任何信息(因为任何周期或非周期函数都可以表示为不同频率的正弦函数和余弦函数之和的形式)。实际上,空间域滤波和频率域滤波经常是对应的:
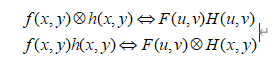
空间滤波实际上是图像与各种空间滤波器(模板)的卷积,而空间卷积的傅里叶变换是频率域中相应变换的乘积,因此频率域滤波可以用图像的傅里叶变换乘以相应的频率域滤波器。
连续变量函数的傅里叶变换暂且不提,我们直接来看图像的二维离散傅里叶变换,令f(x,y)表示一幅大小为[M,N]像素的数字图像,由F(u,v)表示图像的二维离散傅里叶变换(DFT):

指数项由欧拉公式获得,可以将其展开为正弦函数和余弦函数,频率域是使用u和v作为(频率)变量,由F(u,v)构成坐标系。由u和v构成的大小为[M,N]的矩形区域称为频率矩形,大小和输入图像的大小相同。
离散傅里叶反变换(IDFT)的形式为:

频率域原点处变换的值(F(0,0))称为傅里叶变换的直流分量,不难看出,F(0,0)等于f(x,y)平均值的M*N倍。还需要注意的是即使f(x,y)是实函数,它的变换通常也是复数。因此,傅里叶变换常用的是F(u,v)的频谱和相角,并将其显示为一幅图像。matlab有专有的快速傅里叶变换(FFT)算法实现,可以直接调用:F=fft2(f)。一般来说,使用傅里叶变换滤波时,需要对输入数据进行0填充:F=fft2(f,P,Q),结果函数的大小为P*Q。令R(u,v)和I(u,v)表示其实部和虚部,则傅里叶频谱(幅度)为:
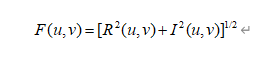
?
傅里叶谱可以通过函数abs直接获得:S=abs(F)。变换的相角定义为:
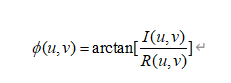
相角可以用atan2调用:phi=atan2(imag(F),real(F));或者直接使用函数angle:phi=angle(F)。有些地方还会提到功率谱,其实就是频谱的平方。实函数的傅里叶变换是关于原点共轭对称的,因此频谱是关于原点偶对称的,而相角是关于原点奇对称的。由此得出的结论是傅里叶变换在u,v方向上是无穷周期的,而通过反变换得到的图像也是无穷周期的,我们感兴趣的是在区间[0,M-1]上的一个完整周期,变换之前,通过将f(x,y)乘以(-1)^(x+y)可以得到期望的周期,调用fftshift可以实现。最重要的是零频率项与f(x,y)的平均值成正比:

?傅里叶变换后,频率矩阵的原点不在中心,可以使用函数fftshift将变换的原点移动到频率矩形的中心:Fc=fftshift(F);与中心处亮度值占支配地位的8位显示相比,谱中的范围很大,显示不明显,通过对数变换可以解决这个问题:S2=log(1+abs(Fc))。
二、实验代码
平滑图像:频率域平滑低通滤波代码如下所示:
%频率域巴特沃斯低通滤波
function test3_pinyulv(picname)
I=imread(picname);
imshow(I);title('原图');
figure;
I_G=imnoise(I,'gaussian',0,0.02);%叠加均值为0,方差为0.02的高斯噪声
subplot(221);imshow(I_G);title('单独叠加高斯噪声后');
I_S=imnoise(I,'salt & pepper',0.04);%叠加密度为0.04的椒盐噪声
subplot(222);imshow(I_S);title('单独叠加椒盐噪声后');
R=I_G(:,:,1);r=double(R);Rr=fft2(r);
G=I_G(:,:,2);g=double(G);Gg=fft2(g);
B=I_G(:,:,3);b=double(B);Bb=fft2(b);%傅里叶变换
Rr=fftshift(Rr);Gg=fftshift(Gg);Bb=fftshift(Bb);%转换数据矩阵
result_R=bw2(Rr);result_G=bw2(Gg);result_B=bw2(Bb);%二阶巴特沃斯低通滤波
result_R=ifftshift(result_R);result_G=ifftshift(result_G);result_B=ifftshift(result_B);
result_r=ifft2(result_R);result_g=ifft2(result_G);result_b=ifft2(result_B);%傅里叶反变换
result_r=uint8(real(result_r));result_g=uint8(real(result_g));result_b=uint8(real(result_b));
I1=cat(3,result_r,result_g,result_b);% 联结
R=I_S(:,:,1);r=double(R);Rr=fft2(r);
G=I_S(:,:,2);g=double(G);Gg=fft2(g);
B=I_S(:,:,3);b=double(B);Bb=fft2(b);%傅里叶变换
Rr=fftshift(Rr);Gg=fftshift(Gg);Bb=fftshift(Bb);%转换数据矩阵
result_R=bw2(Rr);result_G=bw2(Gg);result_B=bw2(Bb);%二阶巴特沃斯低通滤波
result_R=ifftshift(result_R);result_G=ifftshift(result_G);result_B=ifftshift(result_B);
result_r=ifft2(result_R);result_g=ifft2(result_G);result_b=ifft2(result_B);%傅里叶反变换
result_r=uint8(real(result_r));result_g=uint8(real(result_g));result_b=uint8(real(result_b));
I2=cat(3,result_r,result_g,result_b);
subplot(223);imshow(I1);title('巴特沃斯低通滤波后的高斯噪声图像');
subplot(224);imshow(I2);title('巴特沃斯低通滤波后的椒盐噪声图像');
end
其中巴特沃斯低通滤波代码函数如下所示:
function [result]=bw2(data)
[M,N]=size(data);
nn=2;%二阶巴特沃斯低通滤波器
d0=0.15*M;%截止频率15%的图像宽度
m=fix(M/2);n=fix(N/2);
result=zeros(M,N);
for i=1:M
??? for j=1:N
??????? d=sqrt((i-n)^2+(j-n)^2);
??????? h=1/(1+0.414*(d/d0)^(2*nn));%计算低通滤波器传递函数
??????? result(i,j)=h*data(i,j);
??? end
end
end
锐化图像:频域率锐化图像代码如下所示:
%使用拉普拉斯算法对图像进行锐化操作
function test3_pinyulvlvbo_ruihua(picname)
I=imread(picname);
h1=[0,-1,0;-1,5,-1;0,-1,0];%5邻域
h2=[-1,-1,-1;-1,9,-1;-1,-1,-1];%8邻域 滤波算子系数之和为1
BW1=imfilter(I,h1);
BW2=imfilter(I,h2);%滤波操作
figure;imshow(I);title('原图');%显示图像
figure;subplot(121);imshow(uint8(BW1));title('五邻域锐化');
subplot(122);imshow(uint8(BW2));title('八邻域锐化');
end
三、实验结果及分析
频率域巴特沃斯低通滤波结果如下:

?
由于噪声主要集中在高频部分,为去除噪声可以采用低通滤波器来抑制高频部分,同时,由于边缘信息也分布在高频部分,频域滤波法同样会使得图像边沿模糊
频域率拉普拉斯算子锐化图像如下图所示:
?
?
?
可以看出,八邻域相较于五邻域锐化效果更好,且对于拉普拉斯算子而言,其滤波算子系数之和为1。