第二章数字图像基础

了解人眼的结构及视觉模型
学习光度学、色度学的基本知识
了解数字图像的获取、采样、量化的基本原理
简单介绍图像存储格式。
了解不同的图像类型的数据特点

1.人眼的结构及视觉模型

视网膜的接收器(感光细胞层)可以分成两种，分别是锥状体和杆状体

锥状体(cones)─
600~700万，位于中央凹，对颜色高度敏感，可充分分辨图像细节。但只在高照度下提供视觉响应，因此锥状体视觉称为白昼视觉或者亮视觉。

杆状体(rods)─
7500~1500万广泛分布在视网膜表面。感光能力强于锥状体，能够在低亮度环境反应明暗的信号，提供类似单色的「黑白」视觉，不能区分颜色，细节感知能力不如锥状体。杆状体视觉称为暗视觉或微光视觉。

可见光(visible light)或是物体反射可见光进入人的眼睛，光线由角膜(cornea)的折射→穿透内部的水样液(aqueous humor)→调整光量的虹膜(Iris)与瞳孔 (pupil)→透过负责调节功能的水晶体(lens)→再汇聚穿透大片的玻璃体液 (vitreous humor)→落入视网膜(retina)上，我们的凝视点落于视网膜上的中央凹 (fovea)及其附近区域。

当晶状体的折射能力由最小变到最大时，晶状体的聚焦中心与视网膜之间的距离
由17mm缩小到14mm。当眼睛聚焦到远于3m的物体时，晶状体的折射能力最弱，当聚焦到非常近的物体时，其折射能力最强。
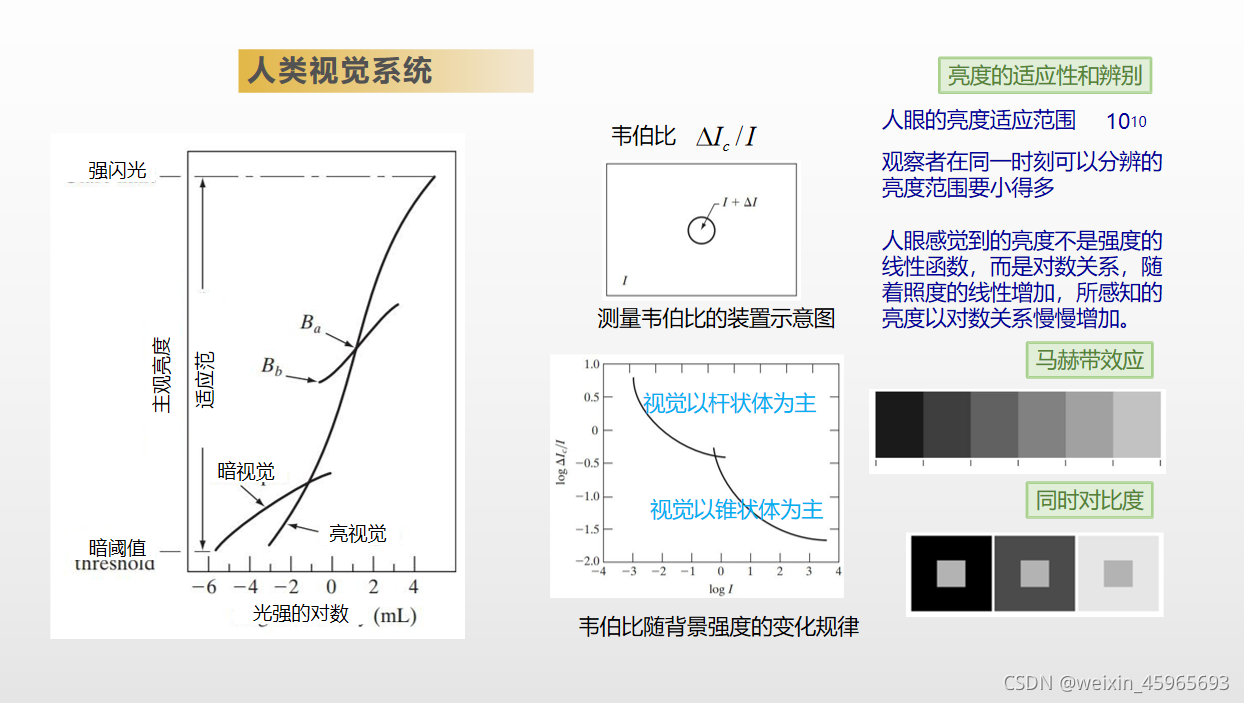
在这里插入图片描述
人眼感受亮度与强度是对数关系，同一时刻可以分辨的亮度范围小得多
韦伯比：△Ic照射分量，是背景照明为I时可辨别照明增量的50%，I照射强度，较小的韦伯比意味着有较好的亮度辨别能力
所谓“马赫带效应（Mach band effect）”是指视觉的主观感受在亮度有变化的地方出现虚幻的明亮或黑暗的条纹，马赫带效应的出现是人类的视觉系统造成的。

2.数字图像的获取、采样、量化的基本原理

2.1光和电磁波谱

没有颜色的光称为单色光或无色光。其唯一属性是光强，或灰度级。
单色图像因为只有灰度级的变换，也称为灰度图像。
发光强度：物理能量
光通量：观察者感受到的光能量
亮度：光感知的主观描绘。

对于单色图像
$L_{min}\leq f(x,y)\leq L_{max}\\ L_{min}=i_{min} r_{min}\quad L_{max}=i_{max} r_{max}$
$0<i(x,y)<\infty$ 入射光强
$0 < r < 1$ 反照率
$L_{min},L_{max}]灰度级$
实际中常常将之线性变换到[0, L -1]
其中0是黑色，L-1是白色。

2.取样和量化的基本概念

空间采样：空间坐标的离散化称为空间采样。图像的空间分辨率主要由采样决定。
灰度量化：灰度的离散化称为灰度量化。图像的幅度分辨率主要由量化决定。
采样不足可能造成图像粒子变粗，产生方块效应。
量化不足可能造成图像中虚假轮廓。

空间分辨率：单位距离的黑白线条对的数量。lpi 是每英寸的线数。单位距离的像素的数量。dpi是每英寸的像素数。
1 lpi = 2 dpi
灰度分辨率：灰度级中可分辨的最小变化。基于硬件考虑，通常灰度级为2的整数次幂。计算机屏幕用8bit量化, 通用的彩色照片每个色彩通道都是8bit的原因。遥感图像的数据常用 16bit量化。

图像的数字表示：假设1幅连续图像f(x，y)等间距采样，获得M行N列
$y)=\left[\begin{array}{cccc} f(0,0) & f(0,1) & \cdots & f(0, \mathrm{~N}-1) \\ f(1,0) & f(1,1) & \cdots & f(1, \mathrm{~N}-1) \\ \vdots & \vdots & \cdots & \vdots \\ f(\mathrm{M}-1,0) & f(\mathrm{M}-1,1) & \cdots & f(\mathrm{M}-1, \mathrm{~N}-1) \end{array}\right]$
G为离散灰度级数，一般取2的整数幂， $G=2^k$ ，则存储1幅图像所需的比特(Bit)数为b=M X N X k。例如百万像素1000X1000，256级灰度级图像所用的比特数为八百万。

分辨率与物理尺寸换算
图像分辨率表示为单位长度的点数，它确定了一个像素对应的物理尺寸。
dpi:dot per inch,每英寸的点数
1inch=2.54cm=25.4mm
分辨率仅在涉及到输入输出设备的时候才有意义。例如，扫描仪的分辨率决定了1inch的照片扫描成数字图像后对应的像素数；对像素数已知的数字图像，图像的分辨率决定了打印后在纸上图像的物理尺寸。
$d p i = 像素数 / 物理尺寸（英寸数）$

图像内插
讨论图像放大收缩导致的内插，由于其结果改变了分辨率，故又称重采样
最近邻插值法 $v (x, y) = f ([x + 0.5], [y + 0.5])$
双线性插值法 $v (x, y) = a x + b y + c x y + d$
三线性插值法 $v(x,y)=\sum_{i=0}^2\sum_{j=0}^3a_{i.j}x^{i}y^{j}$
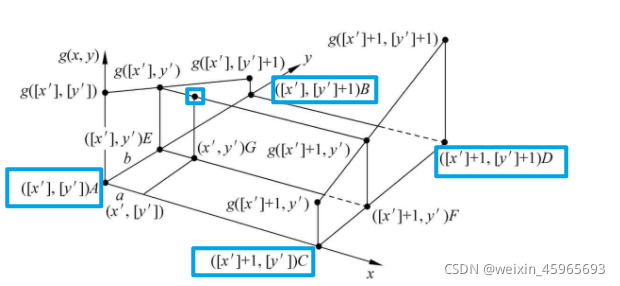
在这里插入图片描述

像素间的基本关系
欧氏距离 $D_{E}(p,q)=\sqrt{(x_{p}-x_{q})^2+(y_{p}-y_{q})^2}$ 相同距离的点近似圆
D4距离或城区距离 $D_{4}(p,q)=|x_{p}-x_{q}|+|y_{p}-y_{q}|$ 相同距离的点近似菱形
D8距离或棋盘距离 $D_{8}=max(|x_{p}-x_{q}|,|y_{p}-y_{q}|)$ 相同距离的点近似方形

图像算术操作
逐像素的加减乘除
加操作的去噪效果：
假设 $g (x, y)$ 是在 $f (x, y)$ 基础上叠加了一个加性噪声 $g(x,y)=f(x,y)+\eta(x,y)$
则叠加K次观测图像后 $\bar g(x,y)=\frac{1}{K}\sum_{i=1}^{K}g_{i}(x,y)$
其期望为 $E{\bar g(x,y)}=f(x,y)$
方差和标准差分别为 $\sigma^{2}_{\bar g(x,y)}=\frac{1}{K}\sigma^2_{\eta}(x,y),\sigma_{\bar g(x,y)}=\frac{1}{\sqrt{K}}\sigma_{\eta}(x,y)$
标准差随叠加的次数而减小，说明有去噪效果
减操作用于增强差异
使用相乘和相除来校正阴影