5.1 神经元模型

这是生物上神经元的一个作用。
M-P精神元模型
1943年,Miculloch和Pitts受到生物神经网络启发,将生物上的神经元情形抽象,提出了机器学习中的“M-P神经元模型”。如图所示
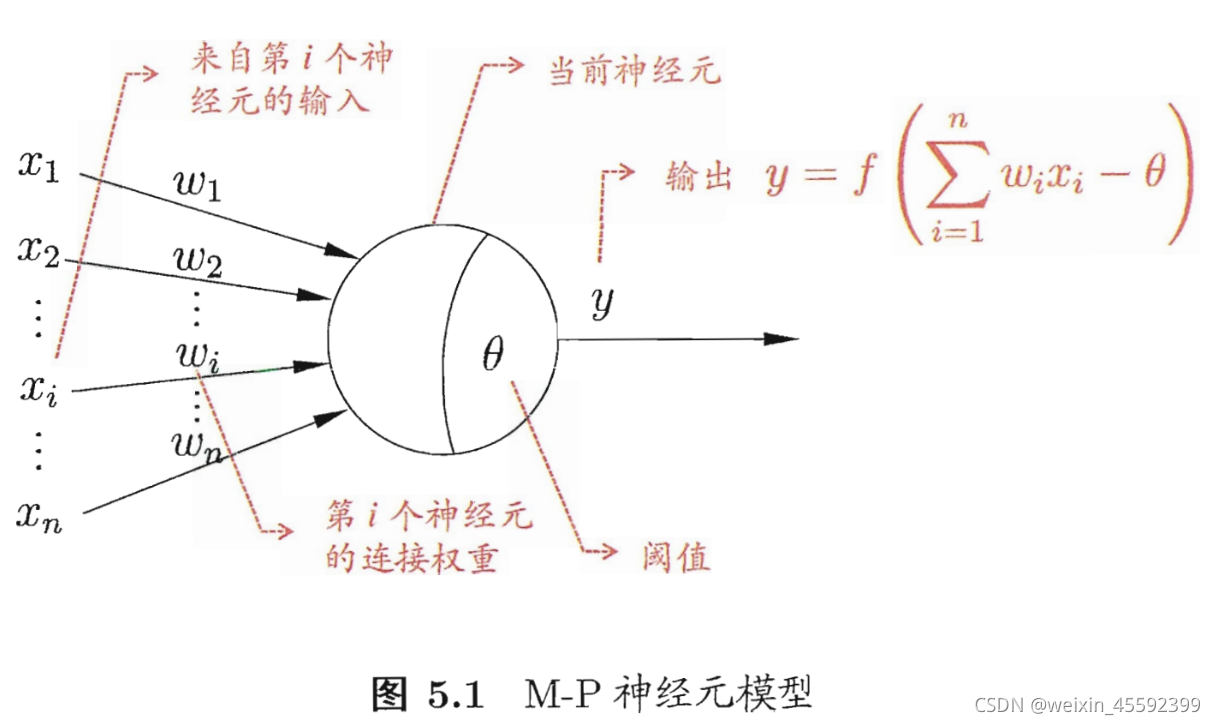

①这里的xi就表示来自第i个神经元的输入。这个神经元会收到n个来自其他神经元传递过来的输入信号。与前面线性回归中一个样例有n维属性相同。
②每一个输入进来的信号都有相应的权重w,因此输入进来n个输入的时候。就会计算出一个加权和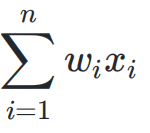
③神经元会有一个阈值。加权和与阈值比较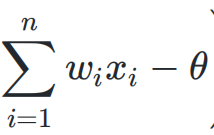
④通过激活函数处理产生神经元的输出,也就是f()
激活函数
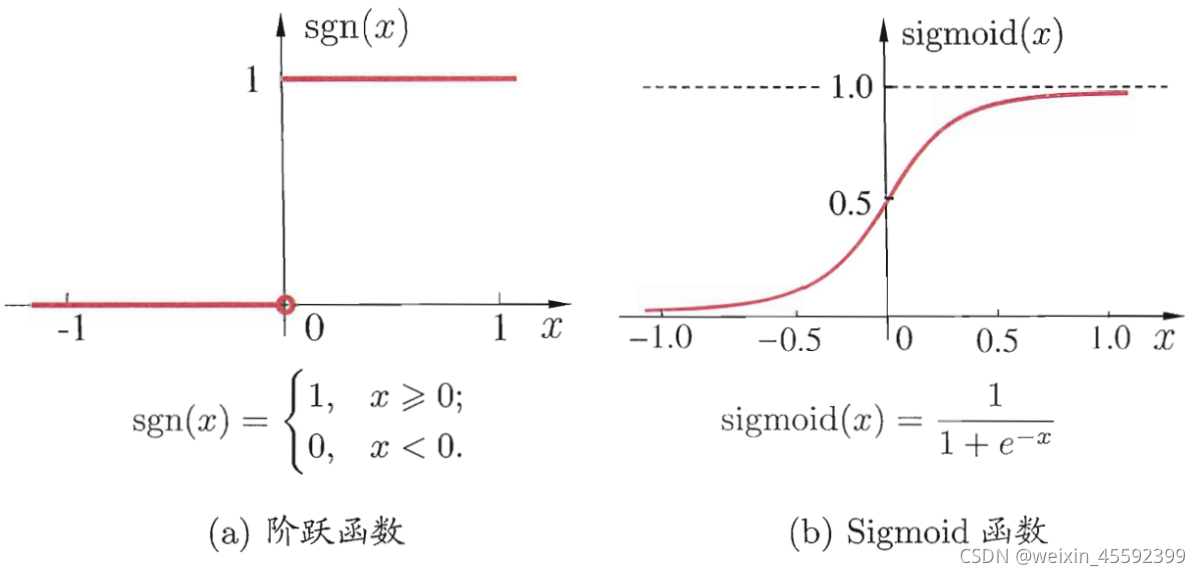
M-P神经元模型最理想的激活函数是阶跃(sgn)函数,它将神经元输入值与阈值的差值映射为输出值“0”或“1”。
然而阶跃函数不连续,不光滑,故在M-P神经元模型中,实际是采用Sigmoid函数来作为激活函数的, Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内,所以也称为挤压函数(squashing function)。
事实上在对数几率回归那里我们也是使用sigmoid函数代替了阶跃函数。
它们的图形如图所示
5.2 感知机
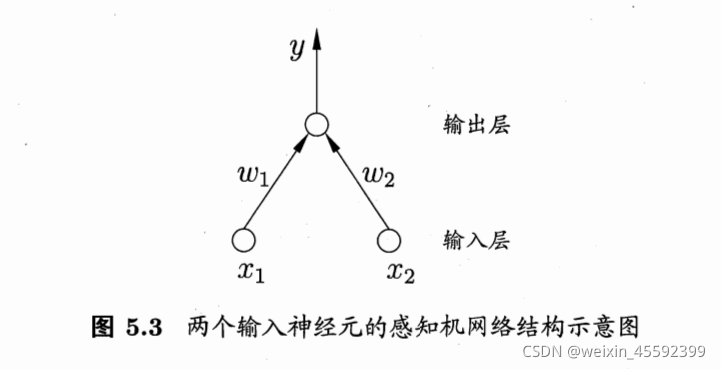
感知机是由两层神经元组成的。
输入层接收外界输入信号后传递给输出层。
输出层是一个M-P神经元。
显然,输出层会输出激活函数处理后的y值
感知机(模型)
感知机模型:使用的激活函数是sgn(阶跃函数)的神经元
显然,其结果会输出0或1,属于分类任务
损失函数(策略)

我们希望错误集合的值最小。也就是求损失函数的最小值。
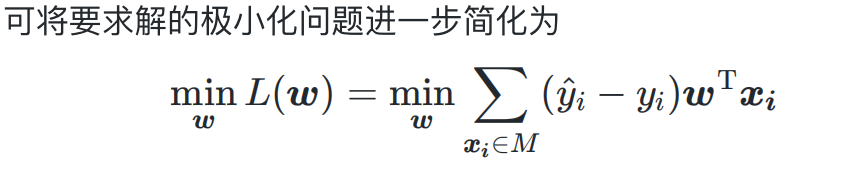
随机梯度下降法(算法)
区分梯度下降法和随机梯度下降法
梯度下降法;是对所有样本求梯度
随机梯度下降法:是随机挑选一个样本进行梯度下降
感知机学习算法使用的是随机梯度下降法
步骤1:首先对损失函数求偏导,得
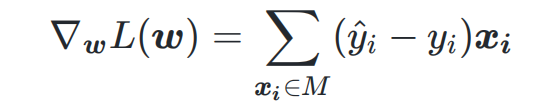
步骤2:一次随机选取一个误分类点使其梯度下降。更新权重:
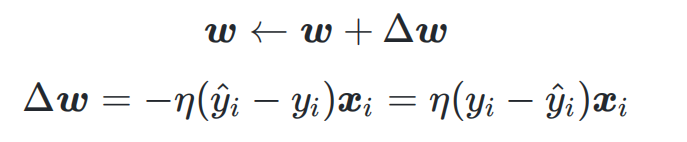
相应地, 中的某个分量 的更新公式即为西瓜书公式(5.2),最终解出来的 通常不唯 一。

5.3 误差逆传播算法(BP算法)
神经网络
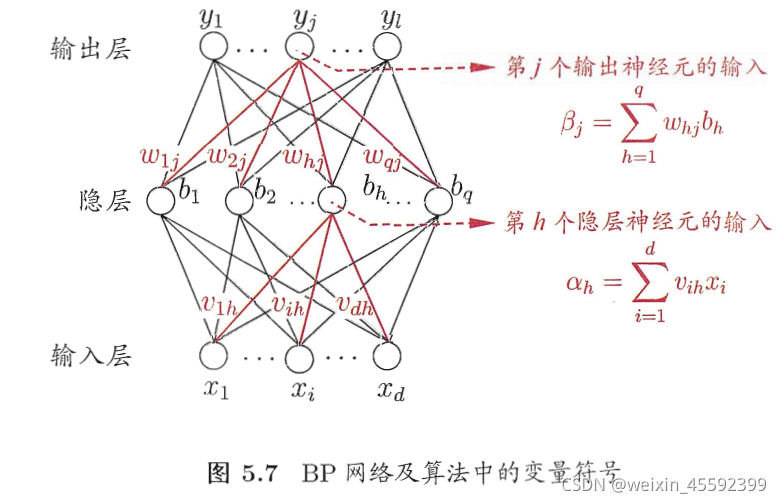

BP算法

步骤:
1.计算输出层误差
2.误差反向传播
3.更新权重值和阈值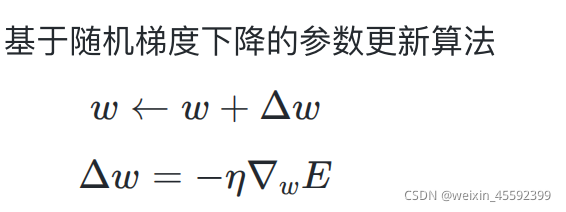
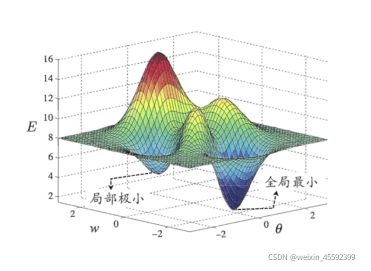
全局最小与局部极小
局部极小:参数空间中的某个点,其领域点的误差函数值均不小于该点的函数值;
全局最小:参数空间中所有点的误差函数值均不小于该点的误差函数值;
实际上我们求得的都是局部最小点。求出的该点也无法直接判断。而是通过在测试集中进行测试而观察该点的情况。