机器学习(第五章)5.深度学习
5.1神经元模型
1.神经网络:神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
2.神经网络中最基本的成分是神经元模型,沿用至今 的是**“M-P 神经元模型“,神经元收到来自n个其他神经元传递过来的输入信号**,这些输入信号通过带权重的连接(connection) 进行传递,神经元接收到的总输入值将与神经元的阀值进行比较,然后通过"激活函数” (activation function 处理以产生神经元的输出(通常是给下一个神经元).
y
=
f
(
∑
i
=
1
n
w
i
x
i
?
θ
)
=
f
(
w
T
x
+
b
)
y=f\left(\sum_{i=1}^{n} w_{i} x_{i}-\theta\right)=f\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right)
y=f(i=1∑n?wi?xi??θ)=f(wTx+b)
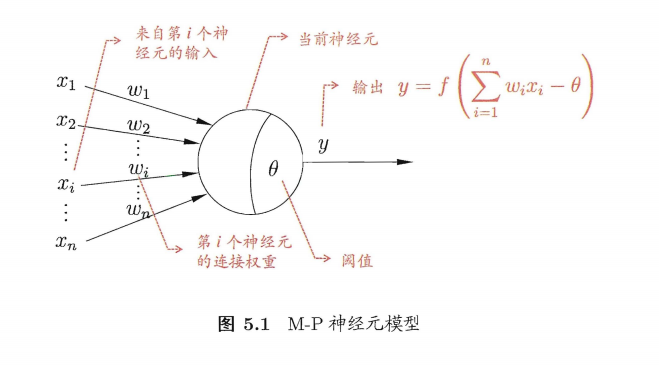
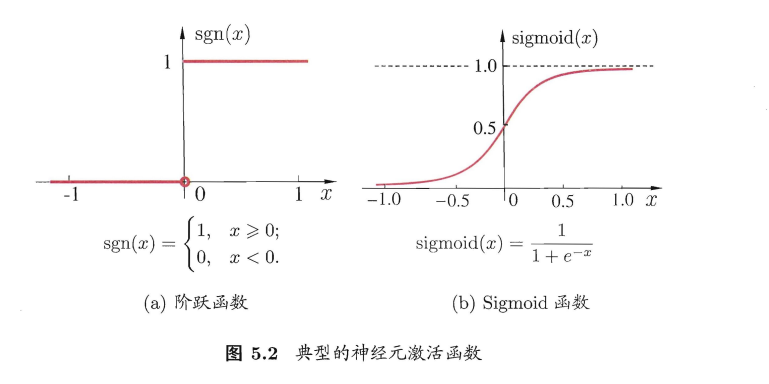
理想中的激活函数是图 5.2(a) 所示的阶跃函数,它将输入值映射为输出值0或者1,显然 “1” 对应于神经元兴奋 ,“0” 对应于神经元抑制。
但是,阶跃函数具有不连续 ,不光滑等不太好的性质,因此实际常 Sigmoid函数作为激活函数,又叫挤压函数
5.2感知机与多层网络
5.1.1感知机模型
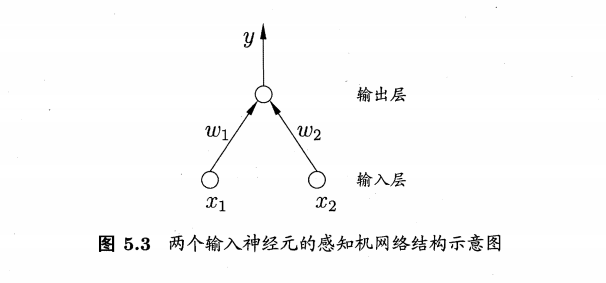
感知机 (Perceptron) 由两层神经元组成, 如下图所示,输入层接收外界输入信号后传递给输出层, 输出层是M-P神经元,亦称"阈值逻辑单元" (threshold logic unit).


5.2.2感知机学习策略


5.2.3感知机学习算法

其中η∈(0,1)为学习率(learning rate) ,其中w通常不唯一,因为损失函数的最小值点不唯一,
5.3神经网络
5.3.1神经网络
像感知机这种单个神经元分类能力有限,只能分类线性可分的数据集,对于线性不可分的数据集,需考虑多个神经元构成的神经网络
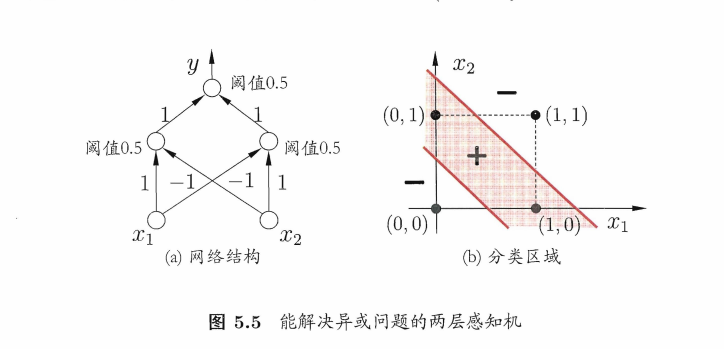
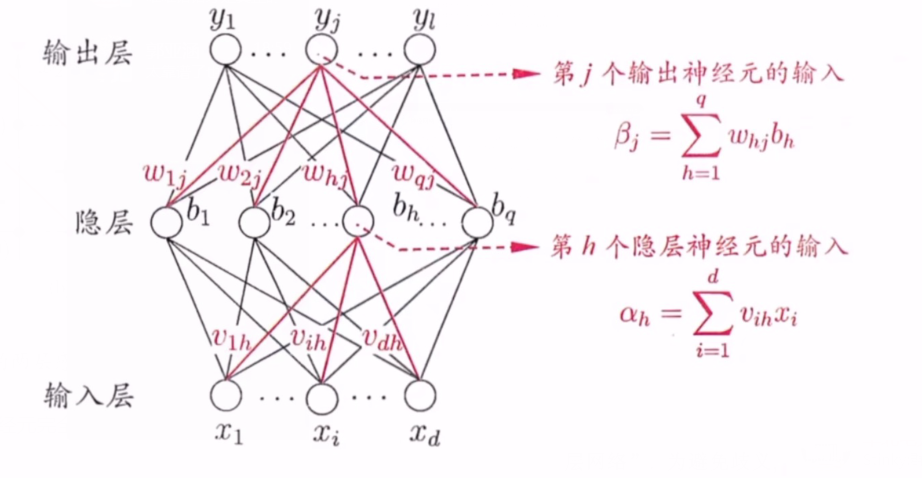
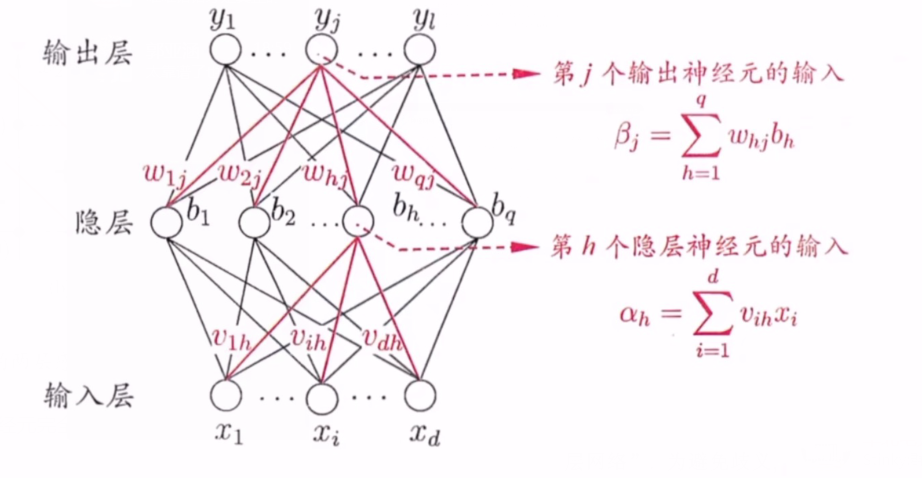
下图这个两层感知机就能解决异或问题。输出层与输入层之见的一层神经元,被称为隐层或隐含层(hidden layer) ,隐含层和输出层神经元都是拥有激活函数的功能神经元.
更常见的是多层前馈神经网络:每层神经元与下一层神经元完全互连,神经元之间不存在同层连接, 也不存在跨层连接。

方便求导,所以在前面乘了指数1/2,平衡掉指数带来的影响
5.3.2误差逆传播算法
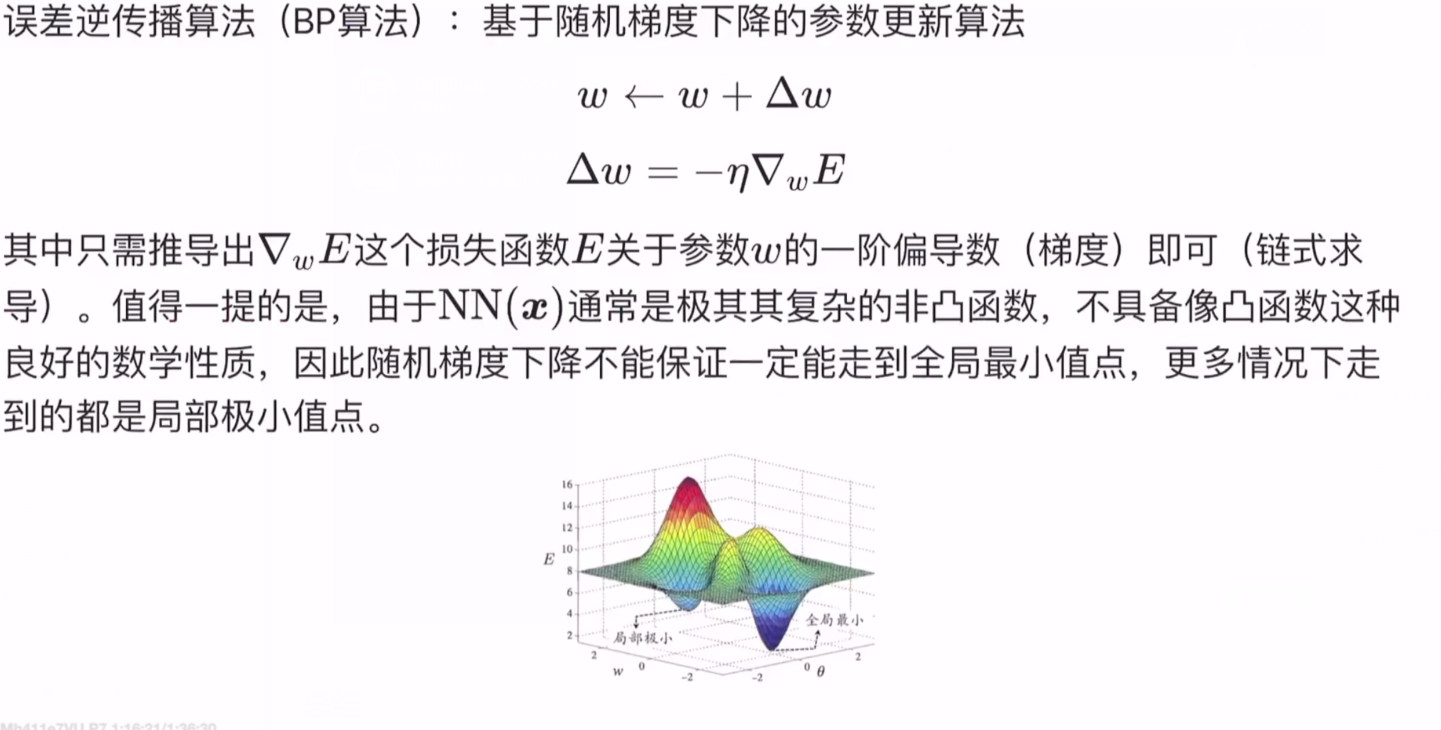
1.误差逆传播算法(BP算法):基于随机梯度下降的参数更新算法
2.下面以输入层第i个神经元与隐层第h个神经元之间的连接权Vih为例:
E k = 1 2 ∑ j = 1 l ( y ^ j k ? y j k ) 2 , Δ v i h = ? η ? E k ? v i h ? E k ? v i h = ∑ j = 1 l ? E k ? y ^ j k ? ? y ^ j k ? β j ? ? β j ? b h ? ? b h ? α h ? ? α h ? v i h \begin{array}{l} E_{k}=\frac{1}{2} \sum_{j=1}^{l}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)^{2}, \Delta v_{i h}=-\eta \frac{\partial E_{k}}{\partial v_{i h}} \\ \frac{\partial E_{k}}{\partial v_{i h}}=\sum_{j=1}^{l} \frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial b_{h}} \cdot \frac{\partial b_{h}}{\partial \alpha_{h}} \cdot \frac{\partial \alpha_{h}}{\partial v_{i h}} \end{array} Ek?=21?∑j=1l?(y^?jk??yjk?)2,Δvih?=?η?vih??Ek???vih??Ek??=∑j=1l??y^?jk??Ek????βj??y^?jk????bh??βj????αh??bh????vih??αh???

求出的是为梯度,基于梯度下降的参数更新算法,需要在加一个负号,再乘以学习率η,最终得
Δ
v
i
h
=
η
e
h
x
i
\Delta v_{i h}=\eta e_{h} x_{i}
Δvih?=ηeh?xi?
同理:
Δ
w
h
j
=
η
g
j
b
h
\Delta w_{h j}=\eta g_{j} b_{h}
Δwhj?=ηgj?bh?
以及第一个阈值和第二个阈值
Δ
γ
h
=
?
η
e
h
Δ
θ
j
=
?
η
g
j
\Delta \gamma_{h}=-\eta e_{h}\\ \Delta \theta_{j}=-\eta g_{j}
Δγh?=?ηeh?Δθj?=?ηgj?
其中
e
h
=
?
?
E
k
?
b
h
?
?
b
h
?
α
h
=
?
∑
j
=
1
l
?
E
k
?
β
j
?
?
β
j
?
b
h
f
′
(
α
h
?
γ
h
)
=
∑
j
=
1
l
w
h
j
g
j
f
′
(
α
h
?
γ
h
)
=
b
h
(
1
?
b
h
)
∑
j
=
1
l
w
h
j
g
j
\begin{array}{c} e_{h}=-\frac{\partial E_{k}}{\partial b_{h}} \cdot \frac{\partial b_{h}}{\partial \alpha_{h}} \\ =-\sum_{j=1}^{l} \frac{\partial E_{k}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial b_{h}} f^{\prime}\left(\alpha_{h}-\gamma_{h}\right) \\ =\sum_{j=1}^{l} w_{h j} g_{j} f^{\prime}\left(\alpha_{h}-\gamma_{h}\right) \\ =b_{h}\left(1-b_{h}\right) \sum_{j=1}^{l} w_{h j} g_{j} \end{array}
eh?=??bh??Ek????αh??bh??=?∑j=1l??βj??Ek????bh??βj??f′(αh??γh?)=∑j=1l?whj?gj?f′(αh??γh?)=bh?(1?bh?)∑j=1l?whj?gj??
学习本 ηε(0, 1) 控制着算沾每一轮迭代中的更新步长,太大则容易振荡,太小则收敛速度又会过过慢,常设置为 η=0. 1.有时为了精细调价,η在Vih和Whj的表达式中取值可以不一样。
3.标准 BP 算法工作流程
对每个训练样例, BP算法执行以下操作:
先将输入示例提供给输入层神经元,然后逐层将信号前传,直到产生输出层的结果;
然后计算输出层的误差(第 4-5 行) ,再将误差逆向传播至隐层神经元(第6行) :
最后根据隐层神经元的误差来别连接权和阈值进行调整(第7行).
该法代过程循环进行,直到达到某些停止条件为止。
4.BP 算法的目标是要最小化训练集上的累积误差
E
=
1
m
∑
k
=
1
m
E
k
E=\frac{1}{m} \sum_{k=1}^{m} E_{k}
E=m1?k=1∑m?Ek?
但"标准 BP 算法"每次仅针对一个训练样例更新连接权和阈值,也就是说,上图算法的更新规则是基于单个的 Ek 推导而得,类似可以推导出基于累积误差最小化的更新规则,就得到了**“累积误差逆传播算法”**。
累积BP算法与标准BP 算法都很常用.
标准 BP 算法
每次更新只针对单个样例,而且参数更新得非常频繁,而且对不同样例进行更新的效果可能出现"抵消"现象.因此,为了达到同样的累积误差极小点 标准 BP 算法往往需进行更多次数的迭代。
累积 BP 算法
直接针对累积误差最小化,它在读取整个训练集一遍后才对参数进行更新,其参数更新的频率低得多.但
在很多任务中,累积误差下降到一定程度之后,进一步下降会非常缓慢,这时标准 BP 往往会更快获得较好的解,尤其是在训练非常大时更明显。
5.有两种策略常用来缓解BP网络的过拟合.
早停:将数据分成训练集和验证集,训练集用来计算梯度、更新连接权和阈值,验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阈值.
正则化:其基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权与阔值的平方和.仍令Ek表示第k个训练样例上的误差,wi叫表示连接权和阈值,则误差目标函数E改变为
E
=
λ
1
m
∑
k
=
1
m
E
k
+
(
1
?
λ
)
∑
i
w
i
2
E=\lambda \frac{1}{m} \sum_{k=1}^{m} E_{k}+(1-\lambda) \sum_{i} w_{i}^{2}
E=λm1?k=1∑m?Ek?+(1?λ)i∑?wi2?
其中 λε(0 1) 用于对经验误差与网络复杂度这两项进行折中,常通过交叉验证法来估计.
5.4全局最小与局部最小
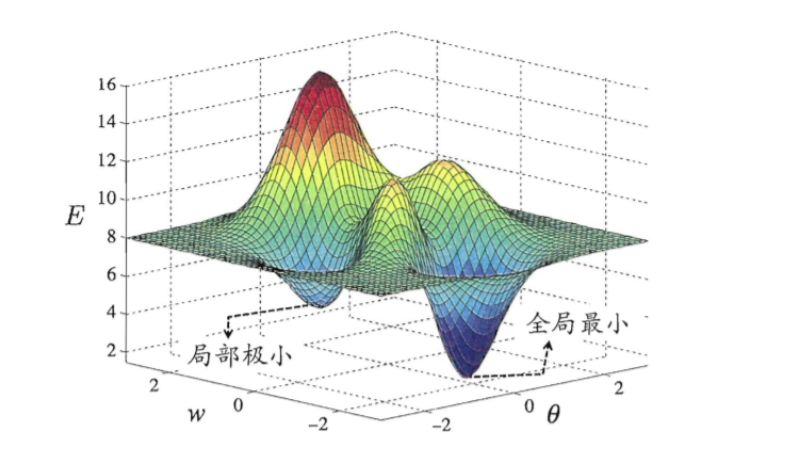
在现实任务中,人们常采用以下策略来试图 "跳出"局部极小,从而进步接近全局最小.
以 不同参数值初始化多个神经网 按标准方法训练后,取其误差小的解作为终参。
使用 “模拟退火” (simulated annealing) 技术,模拟退火在每一步都以一定的概率接受比当前解更差的结果,从而有助"跳出"局部极小
使用随机梯度下降.与标准梯度下降法精确计算梯度不同, 随机梯度下降法在计算梯度时加入了随机因素.于是,即便陷入局部极小点?,它计算出的梯度仍可能不为零, 这样就有机会跳出局部极小继续搜索