一、前言:
自己才接触这一部分,如有错误,大家指出。后续会补充,这个相当于自己学习笔记,便于后面复习。大篇数学公式 真的是。
首先我们要弄明白,什么是特征点:
特征点的组成:
?? ?1.关键点:指特征点在控制里的位置(二维就是图像的位置)
?? ?2.描述子:通常是一个向量,按照某种人为设计的方式,描述了该关键点周围点的信息。相似的特征应该有相似的描述子(即当两个特征点的描述子在向量空间上的距离相近,认为这两个特征点是一样的)
二、估计一个点云的表面法线
参考点云库PCL从入门到精通
在点云特征描述里面,其法向量是非常重要的,怎么求法向量?
表面法线是几何体表面的重要属性,在很多领域都有大量应用,例如:在进行光照渲染时产生符合可视习惯的效果时需要表面法线信息才能正常进行,对于一个已知的几何体表面,根据垂直于点表面的矢量,因此推断表面某一点的法线方向通常比较简单。然而,由于我们获取的点云数据集在真实物体的表面表现为一组定点样本,这样就会有两种解决方法。
? ? ? (1)使用曲面重建技术,从获取的点云数据集中得到采样点对应的曲面,然后从曲面模型中计算表面法线。
? ? ?(2)直接从点云数据集中近似推断表面法线。
确定表面一点法线的问题近似于估计表面的一个相切面法线的问题,因此转换过来以后就变成一个最小二乘法平面拟合估计问题。
因此估计表面法线的解决方案就变成了分析一个协方差矩阵的特征矢量和特征值(或者PCA——主成分分析),这个协方差矩阵从查询点的近邻元素中创建。更具体地说,对于每一个点P,对应的协方差矩阵C如下。

?此处,K是点邻近点的数目,
表示最近邻元素的三维质心,
是协方差矩阵的第j个特征值,
,是第j个特征向量。
算法线的步骤:
( 1)得到p点的最近邻元素
(2)计算p点的表面法线n
(3)检查n的方向是否一致指向视点,如果不是则翻转(法向量的指向正负性)。
PCL代码实现:
#include <pcl/io/io.h>
#include <pcl/io/pcd_io.h>
#include <pcl/features/integral_image_normal.h>
#include <pcl/visualization/cloud_viewer.h>
int
main()
{
//加载点云
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
pcl::io::loadPCDFile("2normal_estimation_using_integral_images/source/table_scene_mug_stereo_textured.pcd", *cloud);
//估计法线
pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
pcl::IntegralImageNormalEstimation<pcl::PointXYZ, pcl::Normal> ne;
ne.setNormalEstimationMethod(ne.AVERAGE_3D_GRADIENT);
ne.setMaxDepthChangeFactor(0.02f);
ne.setNormalSmoothingSize(10.0f);
ne.setInputCloud(cloud);
ne.compute(*normals);
//法线可视化
pcl::visualization::PCLVisualizer viewer("PCL Viewer");
viewer.setBackgroundColor(0.0, 0.0, 0.5);
viewer.addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals);
while (!viewer.wasStopped())
{
viewer.spinOnce();
}
return 0;
}法线可视化:


?
?原始数据:

?正如点特征表示法所示,表面法线和曲率估计是某个点周围的几何特征基本表示法。虽然计算非常快速容易,但是无法获得太多信息,因为它们只使用很少的几个参数值来近似表示一个点的k邻域的几何特征。然而大部分场景中包含许多特征点,这些特征点有相同的或者非常相近的特征值,因此采用点特征表示法,其直接结果就减少了全局的特征信息。因此讨论后面的PPH,PFH
三、Point Pair Feature(PPF)
在上面我们已经解决了法向量的求法
在原论文中,有scene(真实场景点云)?和?model(真实物体模型点云)。其两者点云是通过搭建特征矢量的集合以及每个特征矢量对应的点对集来实现的。m1,m2是两个点,通过这两个点搭建了一个特征描述:![]()
对应图a可知,第一项d是两个点之间的距离,第二项m1的法向量n1与m1与m2连线向量之间的夹角,依次类推。然后将其找到的特征描述类似的放入哈希表,如图b.

?
?说实话,这个我也是没有看的很懂,还是存在很多疑问。我当时是在学习PFH的时候,看其他博客提到了PPH,去查阅了哈,形象理解就是,给你一个目标点云,目标点云,然后先把目标点云的特征点对进行查找,转换为上诉说的特征描述,然后放入哈希表(文章称为:global model description?)进行储存,这里特征描述是对两个点之间的距离,法向量之间的夹角等,看上图b中,(m1,m2)、(m3,m4)、(m5,m6)都是同一个特征描述。然后在对源点云进行一个特征点对的查找,转换为上诉对应的特征描述,将 ??作为 key,搜索 global model description 的哈希表,找到与?
?类似(distance & normal)的 model 特征矢量??和点对??;然后通过找到的每个点对,计算其每一个点对对应的旋转角(有具体的公式,不展开),然后对应最多的旋转角以及点对,作为当前的旋转角(投票机制)。
对于论文的解读:推荐博客:【6D位姿估计】Point Pair Feature (PPF) - 知乎 (zhihu.com)
当然,说这个只是为了引出我所需要的PFH(point featurehistograms)?
四、Point Pair Feature(PPF)
PFH的特征描述与PPH有异曲同工之妙。PFH特征不仅与坐标轴三维数据有关,同时还与表面法线有关。点特征直方图(PFH)表示法是基于点与其k邻域之间的关系以及它们的估计法线,简言之,它考虑估计法线方向之间所有的相互作用,试图捕获最好的样本表面变化情况,以描述样本呢的几何特征。因此,表面法向量估计的质量至关重要。
PFH 特征描述是基于特征点(keypoint)与其邻域点的空间几何关系来编码的。如图1所示,中间红色的特征点作为 query point,在其邻域(指定半径)内搜索 k 个点(蓝色),对于query point 和 k-neighbors 这 k+1 个点,两两配对,可以得到??个点对(point pair)。
?
为了计算两点,和
及与它们对应的法线
,和
,之间的相对偏差,在其中的一个点上定义一个固定的局部坐标系,(这里有点没懂,为什么这个局部坐标系会垂直?):
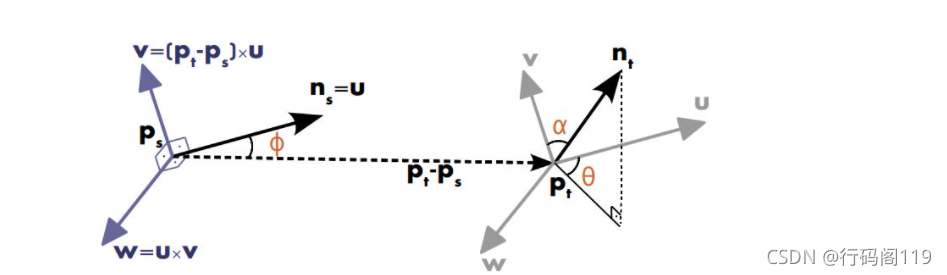
?其中其特征描述子为(和
的偏差可以用一组角度来表示,如下所示):?
?
为了计算查询点??的 PFH 特征,将其邻域??个点对的 quadruplets??特征集合放在一个直方图中,统计投票数量。具体而言,将每个特征划分为 n 个区间,并且统计落在每个子区间的数目,统计落在每个子区间的点数目,因为四分之三的特征在上述中为法线之间的角度计量,在三角化圆上可以将它们的参数值非常容易地归一到相同的区间内。一个统计的例子是:把每个特征区间划分成等分的相同数目,为此在一个完全关联的空间内创建有
个区间的直方图。在这个空间中,每计算一个点对的四个特征值,直方图中对应于该点对的四个特征值特定区间的统计个数加1。如下图所示,就是点云中不同点的点特征直方图表示法的一个例子,在某些情况下,第四个特征量d在通常由机器人捕获的2.5维数据集中并不重要,因为临近点间的距离从视点开始是递增的,而并非不变的,在扫描中局部点密度影响特征时,实践证明省略d是有益的。

?
:有兴趣可以看看??????几何特征系列:Point Feature Histogram(点特征直方图) – LemonC.me
/*
* @Description: 点特征直方图(PFH)描述子 :https://www.codenong.com/cs105922110/
* @Author: HCQ
* @Company(School): UCAS
* @Email: 1756260160@qq.com
* @Date: 2020-10-19 16:37:14
* @LastEditTime: 2020-10-19 18:02:30
* @FilePath: /pcl-learning/10features特征/4点特征直方图(PFH)描述子/PFH1.cpp
*/
#include<iostream>
#include<vector>
#include <pcl/point_types.h>
#include <pcl/features/pfh.h>
#include <pcl/io/pcd_io.h>//点云文件pcd 读写
#include <pcl/features/normal_3d.h>//法线特征
#include <pcl/visualization/pcl_plotter.h>// 直方图的可视化 方法2
using namespace std;
int main(int argc, char** argv)
{
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_ptr(new pcl::PointCloud<pcl::PointXYZ>);
//======【1】 读取点云文件 填充点云对象======
pcl::PCDReader reader;
reader.read("E:/LX/PLC/pcl-learning-master/10features特征/4点特征直方图(PFH)描述子/ism_test_cat.pcd", *cloud_ptr);
// =====【2】计算法线========创建法线估计类====================================
pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;
ne.setInputCloud(cloud_ptr);
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());
ne.setSearchMethod(tree);//设置近邻搜索算法
// 输出点云 带有法线描述
pcl::PointCloud<pcl::Normal>::Ptr cloud_normals_ptr(new pcl::PointCloud<pcl::Normal>);
pcl::PointCloud<pcl::Normal>& cloud_normals = *cloud_normals_ptr;
// Use all neighbors in a sphere of radius 3cm
ne.setRadiusSearch(0.03);//半价内搜索临近点 3cm
// 计算表面法线特征
ne.compute(cloud_normals);
//=======【3】创建PFH估计对象pfh,并将输入点云数据集cloud和法线normals传递给它=================
pcl::PFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::PFHSignature125> pfh;// phf特征估计其器
pfh.setInputCloud(cloud_ptr);
pfh.setInputNormals(cloud_normals_ptr);
//如果点云是类型为PointNormal,则执行pfh.setInputNormals (cloud);
//创建一个空的kd树表示法,并把它传递给PFH估计对象。
//基于已给的输入数据集,建立kdtree
pcl::search::KdTree<pcl::PointXYZ>::Ptr tree2(new pcl::search::KdTree<pcl::PointXYZ>());
//pcl::KdTreeFLANN<pcl::PointXYZ>::Ptr tree2 (new pcl::KdTreeFLANN<pcl::PointXYZ> ()); //-- older call for PCL 1.5-
pfh.setSearchMethod(tree2);//设置近邻搜索算法
//输出数据集
pcl::PointCloud<pcl::PFHSignature125>::Ptr pfh_fe_ptr(new pcl::PointCloud<pcl::PFHSignature125>());//phf特征
//使用半径在5厘米范围内的所有邻元素。
//注意:此处使用的半径必须要大于估计表面法线时使用的半径!!!
pfh.setRadiusSearch(0.05);
//计算pfh特征值
pfh.compute(*pfh_fe_ptr);
cout << "phf feature size : " << pfh_fe_ptr->points.size() << endl;
// 应该与input cloud->points.size ()有相同的大小,即每个点都有一个pfh特征向量
// ========直方图可视化=============================
pcl::visualization::PCLPlotter plotter;
plotter.addFeatureHistogram(*pfh_fe_ptr, 30); //设置的很坐标长度,该值越大,则显示的越细致
plotter.plot();
return 0;
}