[人工智能]Swin Transformer

Swin Transformer

参考视频

1. 回顾 Transformer 和 ViT

要不就不回顾了吧，怪麻烦的。注意一下：

• Transformer 中，Encoder 是有 6 块的，但是输入输出并不改变尺寸。就是输入多大，输出就多大。这也是 Swin TRM 不一样的地方之一。（对应了下面的 1）
• ViT 虽然把 patch 当作一个个 token 进行输入，但是还是会有一个问题，就是如果图片太大的话，那 patch 就会变得很多，那对复杂度还是很不友好。这也是 Swin TRM 要改进的一个点。（对应了下面的 2）

Swin Transformer ( Swin TRM ) 做到了两点：

1. 金字塔形状：在经过一个 Encoder 之后，会做一个 patch merging 的操作，也就是一个降采样的过程。增大了感受野，减小了分辨率。（不是 Encoder 让感受野变大的，是之后的 patch merging）
2. 注意力机制放在一个窗口内部。

先提一嘴，这个窗口内部的注意力是什么？（假设一张图片分成 9 个 patch）

• ViT 是把 9 个 patch 一起输进去（一个 patch 当作一个 token），这样做的不就是整张图片的注意力嘛，但是图片太大，显然不可能一起输进去。
• Swin 是把一个个 patch 单独处理（每个 patch 里面的每个像素当作 token，当然每个像素指的不是一个值，而是$[1,clannels]$）再输进去，这不就是 patch 内部的注意力嘛，把 9 个 patch 当作一个 batch，如果图片很多张的话，就可以把几张图片当成一个大 batch。
  

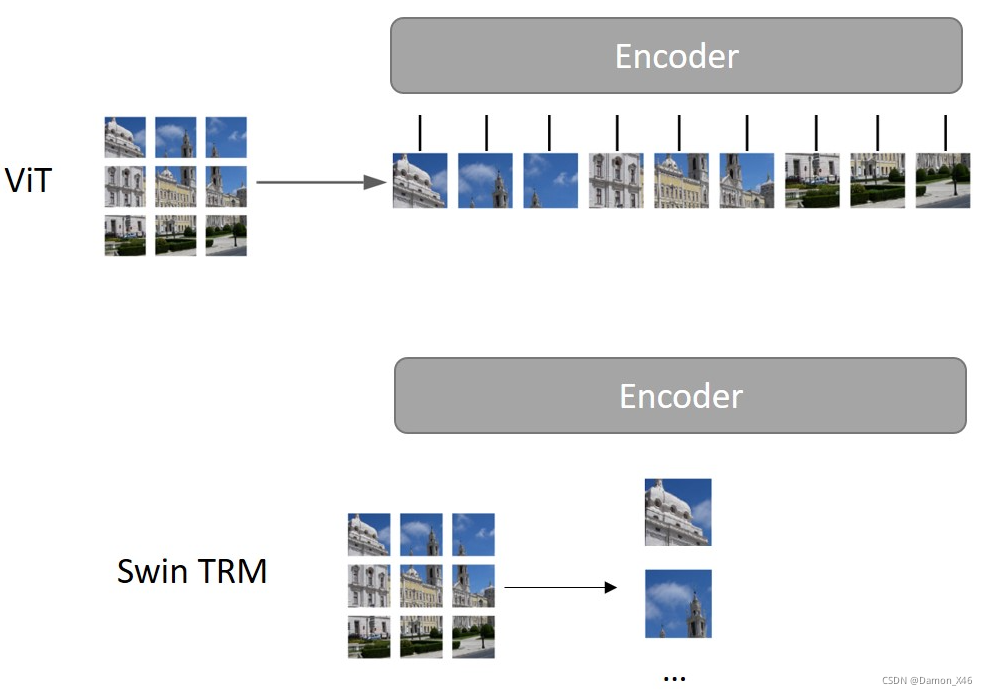
简单来说就是（从 TRM 到 Swin TRM）：

• TRM 用来处理语言啊文字啊之类的，所以可以每个字当作一个 token 输入。
• ViT 如果也把每个像素当作一个 token 的话，太复杂，所以采用的是 patch 的形式。但是对于图片太大的话，那么分出来的 patch 还是太多，还是太复杂。
• Swin TRM 相当于又回到了一开始简单的那个想法，就是把一个个像素当作 token 来输入，因为 patch 很小，所以把像素当作 token 没关系。但是，这样就不能把整张图所有的 patch 一起输进去了， 就要用 patch 去组成 batch。
• （是有点绕啦，但是我听懂了，哈哈哈）
• 时刻注意 Swin TRM 是 patch 中的一个像素是一个 token，而 ViT 中，每个 patch 是一个 token。

2. Swin TRM

2.1. Swin TRM 整体架构

整体的结构如下图所示：

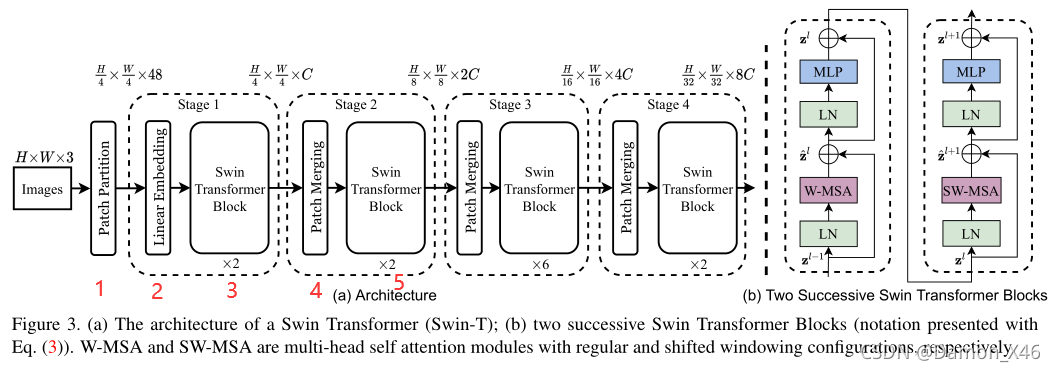
假设输入图像是 $224\times 224\times 3$，那么图中每个部分的输入输出为：

1. $224\times 224\times 3$ 到 $(224/4)\times (224/4)\times (4\times 4\times 3)$
2. $(224/4)\times (224/4)\times (4\times 4\times 3)$ 到 $(224/4)\times (224/4)\times 96$ （假设线性映射是映射到 96）
3. $(224/4)\times (224/4)\times 96$ 到 $(224/4)\times (224/4)\times 96$ （第三个这边下面有一个 $\times 2$，说明是经过两个 block，就是上图右边的那两个 block，那两个其实是不一样的，是两个 Encoder。我们说过，TRM 的 Encoder 是不会改变形状的，所以经过这个之后形状是没有改变的。）
4. $(224/4)\times (224/4)\times 96$ 到 $(224/8)\times (224/8)\times (96\times 2=128)$ （其实这边在下采样的时候是变成了 4，然后 4 再映射到 2 ，所以后面是 $96\times 2=128$）

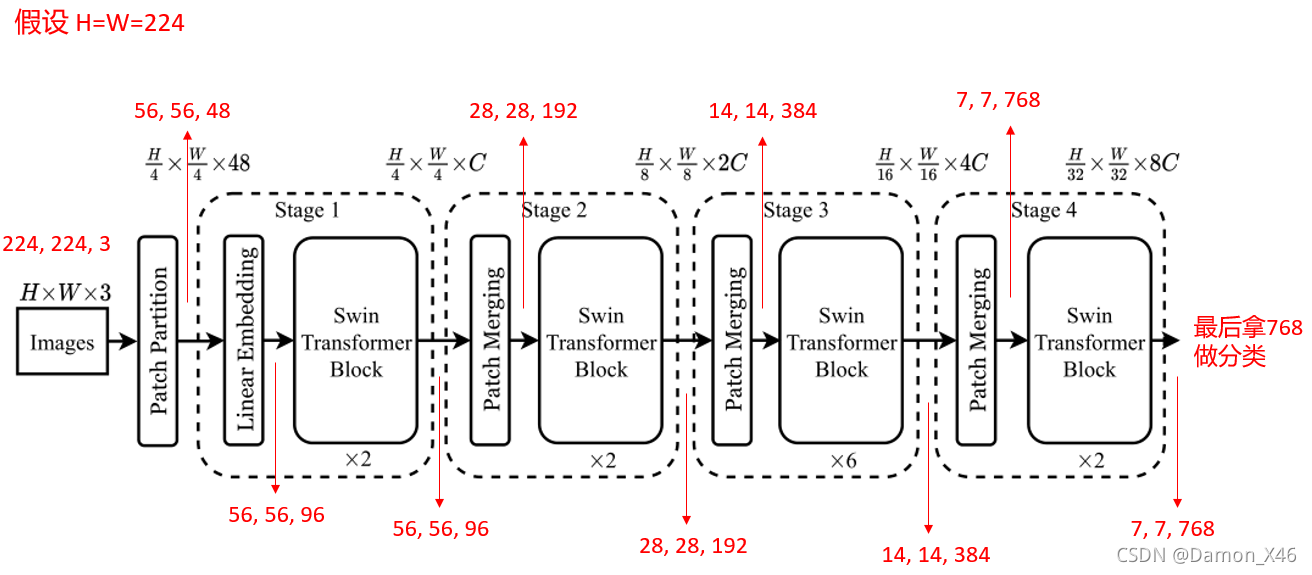
代码实现的时候，其实是下面这个图这么组装的：

2.2. 输入数据处理（框1）

假设图像是 (224, 224, 3)，patch size 是 4，映射的维度是 96。那么第一个框框的操作就是（解决数据输入的问题）：

• 先把 (224, 224, 3) 划分 patch，每个 patch 是 (4, 4, 3)，所以有 3136 个 patch
• 然后把每个 patch 展平到 48（$4\times 4\times 3$）
• 然后把 48 做一个映射，映射到 96

2.3. 相对位置编码和注意力（框2）

Swin TRM 位置编码有两点不同：

1. 加的位置不同，放在了 attention 矩阵中。（公式如下）
2. 使用的是相对位置编码，而不是绝对位置信息

$$Attention(Q,K,V)=SoftMax(Q{K}^T/\sqrt{d}+B)V\text{\hspace{1em}(1)}$$

SoftMax 里面的这个东西的本质是计算每个字符对每个字符的相似性。所以这里面的形状应该是 $[seq.len.\times seq.len.]$ 也就是说，相对位置编码的这个 B 矩阵，也是这个形状。

在图像这里，在 Swin TRM 这里，就是计算一个 patch 里面，像素跟像素之间的相似性，假设现在一个 patch 的大小是 $7\times 7$ 那么这个 B 矩阵的维度就应该是 $49\times 49$，而不是 $7\times 7$（因为 $7\times 7$ 的 patch 里面有 49 个像素呀，计算像素之间的相似性，那这个矩阵就是 $49\times 49$）。

重点哦！！！现在已经知道 B 的形状是什么了，接下来就是了解 B 里面的内容是怎么来的！

2.3.1. 绝对位置信息和相对位置信息

• 绝对位置信息，就是原点没有动。（下图的第一条，(0, 1, 2)）
• 相对位置信息，就是原点动了。（下图三种，(0, 1, 2), (-1, 0, 1), (-2, -1, 0)）
• 而且这里定义的是向右为正，如果规定向左为正，那又是另一种情况。
  
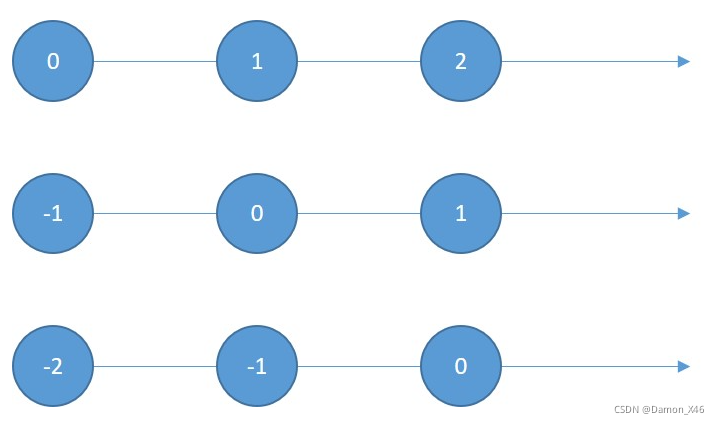
  网格的情况见下：

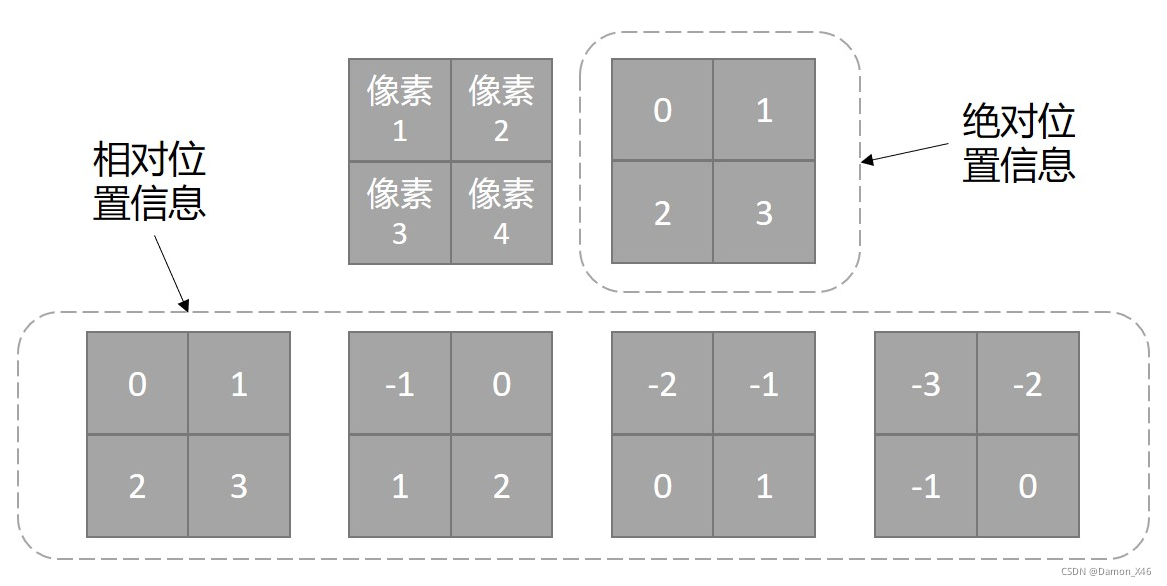
那么问题来了，怎么把相对位置信息融入到 Attention 中？？

2.3.2. 把相对位置信息融入 Attention 矩阵中

接下来还是用假设的方法来解释，先把 Attention 公式再拿下来看一眼：
$$Attention(Q,K,V)=SoftMax(Q{K}^T/\sqrt{d}+B)V\text{\hspace{1em}(2)}$$
用2.3.1. 中的 4 个像素来举例。前面分析过了，4 个像素，B 矩阵的形状就应该是 $4\times 4$，$Q{K}^T/\sqrt{d}$ 的形状跟 B 是一样的，也是 $4\times 4$。我们再假设 $Q{K}^T/\sqrt{d}$ 的值如下所示：

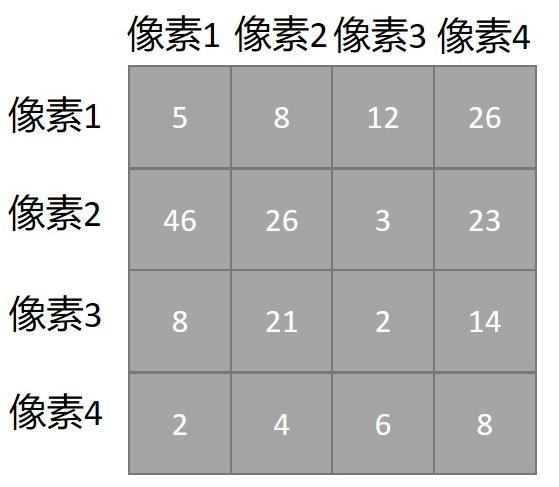
现在的问题就是怎么把上面的 4 个相对位置信息融入到这个 Attention 矩阵中！

我们把第一行看作是以1为原点，以此类推，不就可以把相对位置矩阵融入进去了吗？如下图：

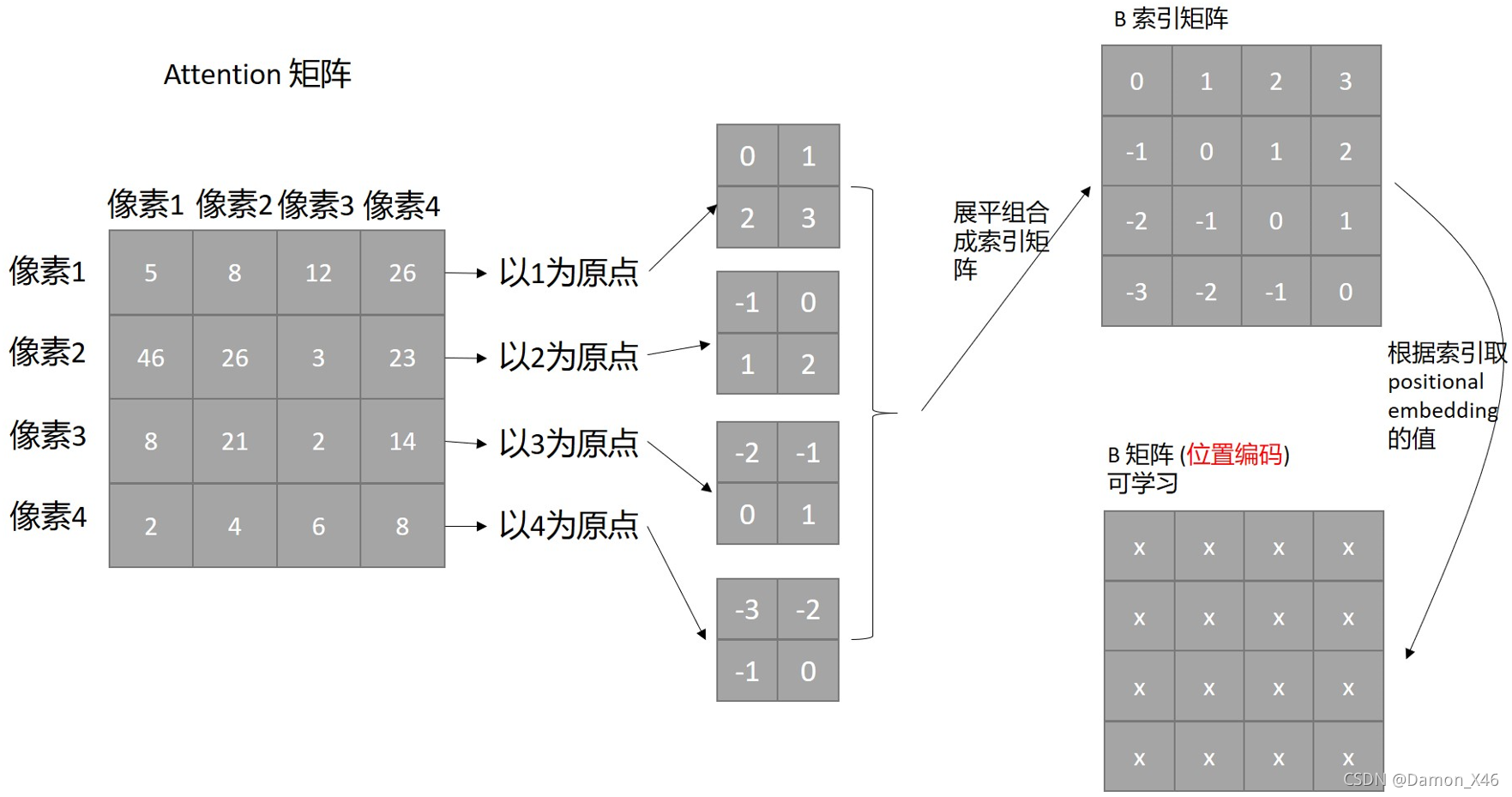
梳理一下：

• 我们现在 4 个像素，有 4 个相对位置的情况
• 4 个情况的相对位置可以展平拼接成一个 $4\times 4$ 的索引矩阵
• QK 做完操作之后有一个 $4\times 4$ 的 Attention 矩阵
• 会初始化一个可以学习的 $4\times 4$ 位置编码矩阵
• 用索引矩阵去位置编码矩阵中取每个像素的位置编码，与 Attention 相应位置的相加
• 这样就能得到最终的 Attention 矩阵
• 然后再 SoftMax，再和 V 加权
• 这样整个 注意力操作就完成了

当然，上面这个只是举例，实际上，Swin TRM 的操作是下面这个图：

其实是一样的，只不过他用的是两个值，稍微复杂了一点而已。
那他用这两个值怎么取索引？很简单的思路就是把这两个值加起来当作索引矩阵再去取值的。（例如上面第一行就会变成 (0, 1, 1, 2)）
但是，这样会有两个问题：

1. 有负数
2. 第一行第二个跟第一行第三个，相对位置信息肯定是不一样的，但是加起来的索引是一样的，取到的值是一样的

所以要进行改进的两个点：

1. 不能有负数
2. 不同位置的相对位置信息不能相同

改进的方法（如下图）：

1. 加一个 $M?1$ ，让他没有负数
2. 在 0 维度上 $\times 2M?1$ 就不一样了

下面的流程就很容易懂了：

然后这个就是相对位置信息了。也就是所谓的 positional embedding。把这玩意儿再加到 Attention 中就可以了。

2.4. 移动窗口注意力机制（框2 & 图(b)）

由上分析可知：目前为止 (严谨吧)，Swin TRM 的注意力只是局部的，只在一个个 patch 之内，缺少交互。所以，这也是 Swin TRM 的改进之一，就是使用了移动窗口注意力。

• 假设，图片大小是 $56\times 56$ ，patch 的大小是 $7\times 7$ ，移动了 $3$ 个像素
• 移动的方法是把图像上面三行的像素放到最下面，左边三列的像素放到最右边。组成一张新的图像
• 这样新图像跟原来的图像在大部分位置就有 $3$ 个位置的偏差。（说的不准确，但是可以这么理解）
• 示意图可以见下面这个，方便描述。

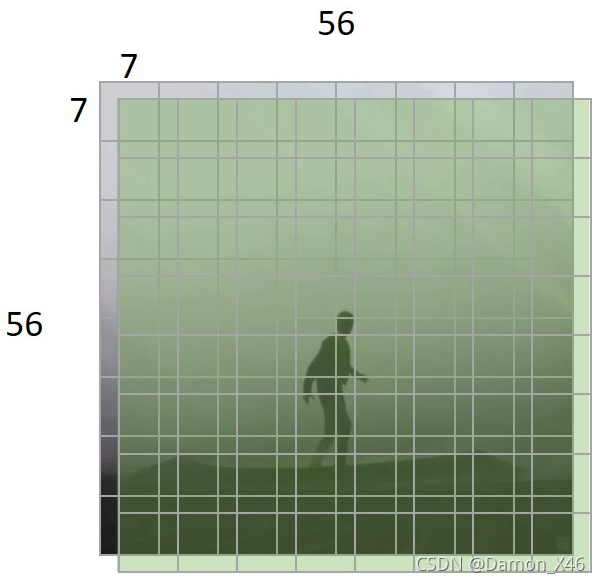
• 就大概像上图这个意思。我们看第一个 patch，灰色的是原图的，绿色的是移动之后的
• 可以看到移动之后的窗口相对于原来的窗口，会跟相邻的三个窗口有重叠，这样在做注意力的时候，就会对相邻的三个窗口内的部分信息一起做注意力。就不会是原来单张图片只在自己 patch 内做注意力这么局限了。
• 这个就是那两个 block，还记得吗，很上面的那张图，划分阶段的那个 ~

但是，问题来了。我们把上面三行跟左边三列的像素分别拿到下面跟右边。窗口大小为 7 的话，最下面跟最右边在对 patch 做操作的时候，就会把原本不相邻的 patch 去做操作。也就是说，本来就不相关的，没有语义联系的几个部分在这里会被计算相关性。首先是没有意义，其次就是会导致网络学习错误的东西。（如下图 1 跟 2，3 跟 6 ，4578，去做 Attention 是不是很不合理，本不相邻）

那么要怎么办呢？下面画出示意图并解释。

• 这边标索引，可以告诉模型，窗口看到的哪些是相邻的，哪些是不相邻的
• 也就是用 masked 的方法
• 往下看就知道了，直接拿右下角那个都不相邻的 $7\times 7$ 窗口来举例

像素点比较多，所以下面，直接把相同的弄在一起来举例

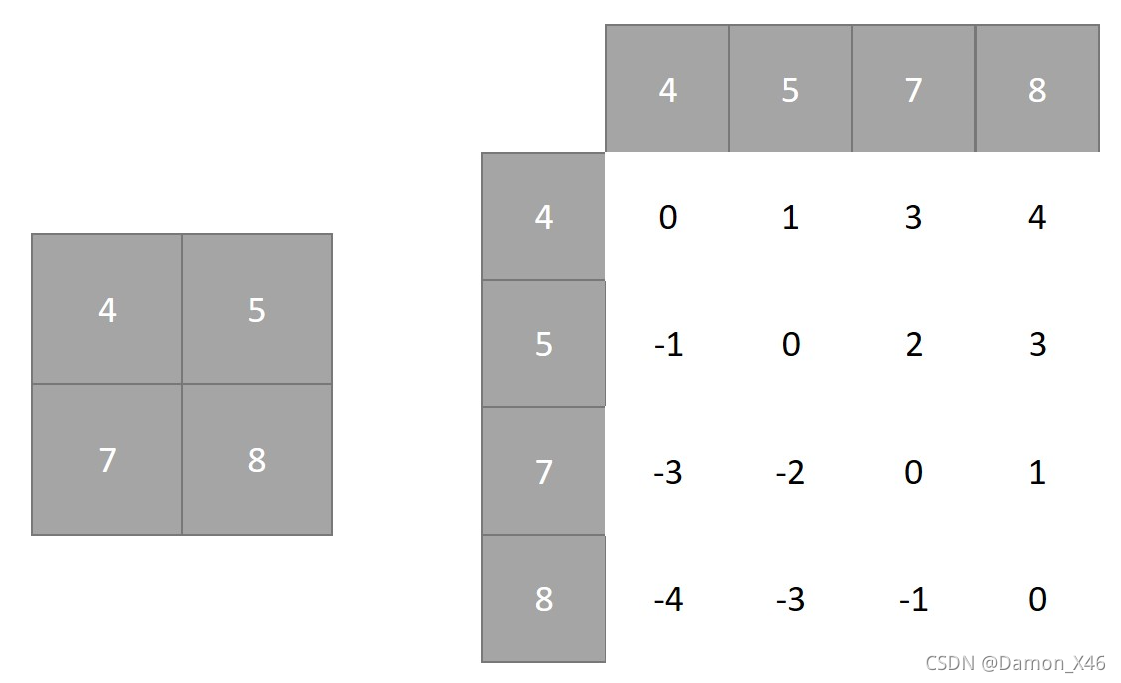
• 如上图所示，拿来相减
• 0 的位置就代表是相邻的位置
• 非 0 的就代表本来没有相邻，但是被框到一起了
• 那么就可以把 0 的部分置 0，把非 0 的部分置为 $?\infty$，或者 $?1000$，$?100$
• 然后再把这个矩阵加到 Attention 矩阵中，这样，不相邻的就 $?$ 很大，那就没有影响或者说影响很小了。（记得 Attention 矩阵吧，值都不是很大）
• 当然这边只是拿的 4 个块合起来举例的，实际上，我们最后面那个是 $7\times 7$ 大小的窗口，展开再相减得到的就是 $49\times 49$ 的矩阵，不就是刚好和 Attention 矩阵的维度一样嘛。（闲着没事干的，可以把上面那个 $7\times 7$ 的矩阵展开看看）
• 一切如此完美 ~

2.5. patch merging

• 把原来的特征图，隔两行，隔两列取样
• 这样得到的就是 4 份原来特征图一半大小的新的特征图
• 然后再用一个 linear 层，把 4 映射成 2
• 所以可以看到上面那个网络结构图的 $C$ 经过一个 patch merging 都是两倍在增长的