最优化记录

文章目录

最优化记录
一、梯度与共轭梯度置于最优化
二、代码实例

一、梯度与共轭梯度置于最优化

到了最优化领域当中，解析法（求导数=0得极值点）已经不能直接应用，因为多维直接解析计算量非常大，由此引申出了迭代法。机器学习的优化算法也可划分到此，不过似乎演化算法与梯度同属优化但内在多种不同。

解析法：
在我们本科学习的高数当中，要想求极小点，首先考虑的便是一阶导数为0的点，同理，高维空间中对应的概念则是梯度为0的点。(不是偏导，而是由所有偏导组成的向量）

在这里插入图片描述
多维空间二次函数的1/2在这里没有很大的特殊意义，只是为了再对X²进行求导后多出来的2系数进行抵消。

迭代公式：X^k+1=X^k + a^kd^k

最速下降法: 方向d为负梯度方向步长a可以利用局部极小点的一阶必要条件

共轭梯度法:定义两个向量d1,d2,矩阵Q。d1Qd2=0。则d1与d2方向共轭。在优化中则可以理解为上一次搜索方法与这一次的应当方向共轭。即d^k与d^k+1方向共轭。但由于初始方向d⁰往往是负梯度方向，故而共轭梯度。

（共轭梯度具有二次终结性，即几维空间就迭代几次，属于线性搜索，相较于牛顿法尔和拟牛顿法等超线性方法还是速度慢了）

算法步骤这里直接截图最优化算法导论这本书的算法

在这里插入图片描述

二、代码实例

考虑最优化如下函数：
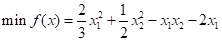
在这里插入图片描述
首先需要将其转换为标准形态

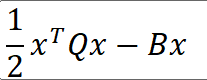
X0作为初始点，利用共轭梯度法进行计算，原题只为2维空间，只需要迭代两次即可

import numpy as np
Q = np.array([[4/3,-1],[-1,1]])
x0 = np.array([[-2],[4]])
B = np.array([[2],[0]])
g0 = np.dot(Q,x0)-B
d0 = -g0
a0 = -( ( g0.T.dot(d0) ) /  (d0.T.dot(Q).dot(d0)) )
x1 = x0+a0*d0
g1 =  np.dot(Q,x1)-B
beta0 = ( g1.T.dot(Q).dot(d0) ) / ( d0.T.dot(Q).dot(d0))
d1 = -g1 + beta0*d0
a1 = -( ( g1.T.dot(d1) ) /  (d1.T.dot(Q).dot(d1)) )
x2 = x1+a1*d1