第五章图像复原

主要内容包括图像的噪声模型、噪声消除

掌握不同的噪声模型的特点和去除噪声的方法，逆滤波、维纳滤波的原理和用法。
理解图像退化和处理的模型。
了解约束最小二乘法滤波，几何变换和图像配准。

第六章小波及对分辨率处理

主要内容包括图像金字塔、对分辨率扩展、小波函数、小波变换。

掌握图像金字塔的形成原理，拉普拉斯金字塔的构成原理。
掌握小波变换的原理和用法。理解小波包的原理和用法。
了解不同类型的小波变换的方法和区别。

多分辨率处理

小结放在前面：
介绍了多分辨率技术中的两个重要技术，图像金字塔和子带编码
基于上述二者引出基于哈尔小波变换的多分辨率分析技术
介绍了二维小波变换的基本原理
给出了小波变换在图像降噪、边缘检测和图像融合上的应用

小波变换
小波的缩放和平移：
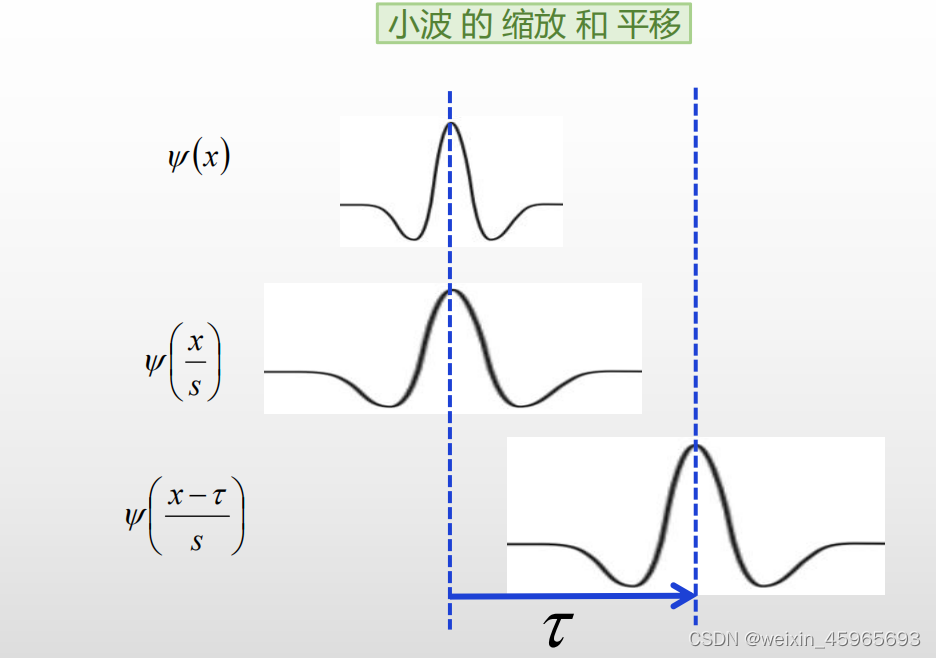
在这里插入图片描述

基函数是小波，具有变化的频率和有限的持续时间
可以获得随时间变化的频谱
小波变换具有良好的局部时频聚焦特性，而被称为“数字显微镜”
傅里叶变换vs小波变换
-傅里叶变换反映的是图像的整体特征，其频域分析具有很好的局部性，但空间（时间）域上没有局部化的功能
-与傅里叶相比，小波变换是空间（时间）和频率的局部变换，它通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。

连续小波变换：
连续平方可积函数 $f (x)$ 的
$\begin{aligned}连续小波变换(CWT)&：W_{\psi}(s,\tau)=\int_{-\infty}^{\infty}f(x)\psi_{s,\tau}(x)dx&其中\psi_{s,\tau}=\frac{1}{\sqrt{s}}\psi(\frac{x-\tau}{s})\\反连续小波变换&：f(x)=\frac{1}{C_{\psi}}\int_{0}^{\infty}\int_{-\infty}^{\infty}W_{\psi}(s,\tau)\frac{\psi_{s,\tau}(x)}{s^2}d\tau ds&其中C_{\psi}=\int_{-\infty}^{\infty}\frac{|\Psi(u)|^2}{|u|}du \end{aligned}$
$\Psi(u)$ 是 $\psi(x)$ 的傅里叶变换

小波函数必须满足的条件：
1.小波必须是振荡的
2.小波的振幅只能在一个很短的一段区间上非零，即是局部化的

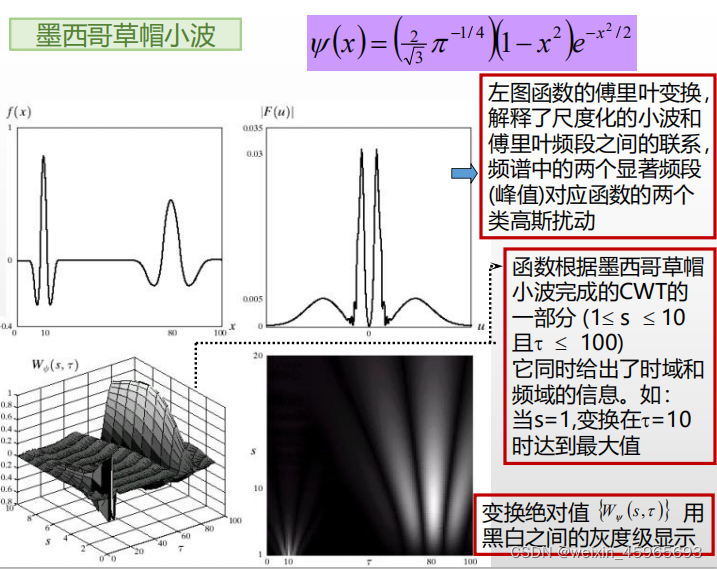
在这里插入图片描述

小波变换是多分辨率理论的分析基础，下面将从多分辨率分析的角度来解释小波变换

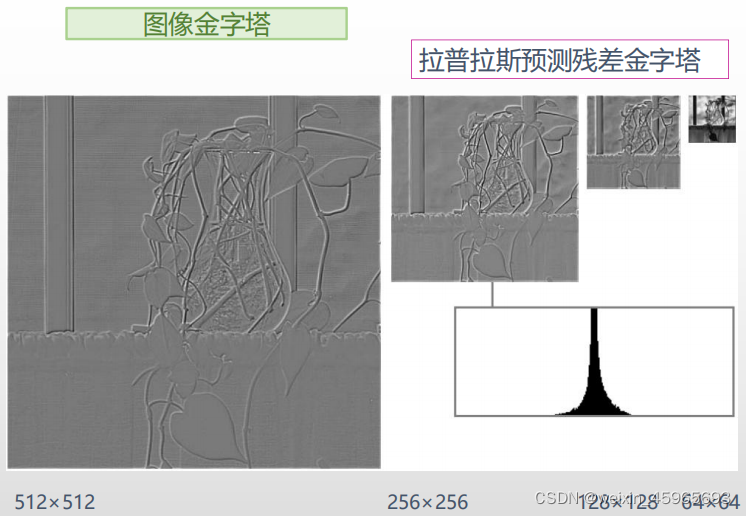
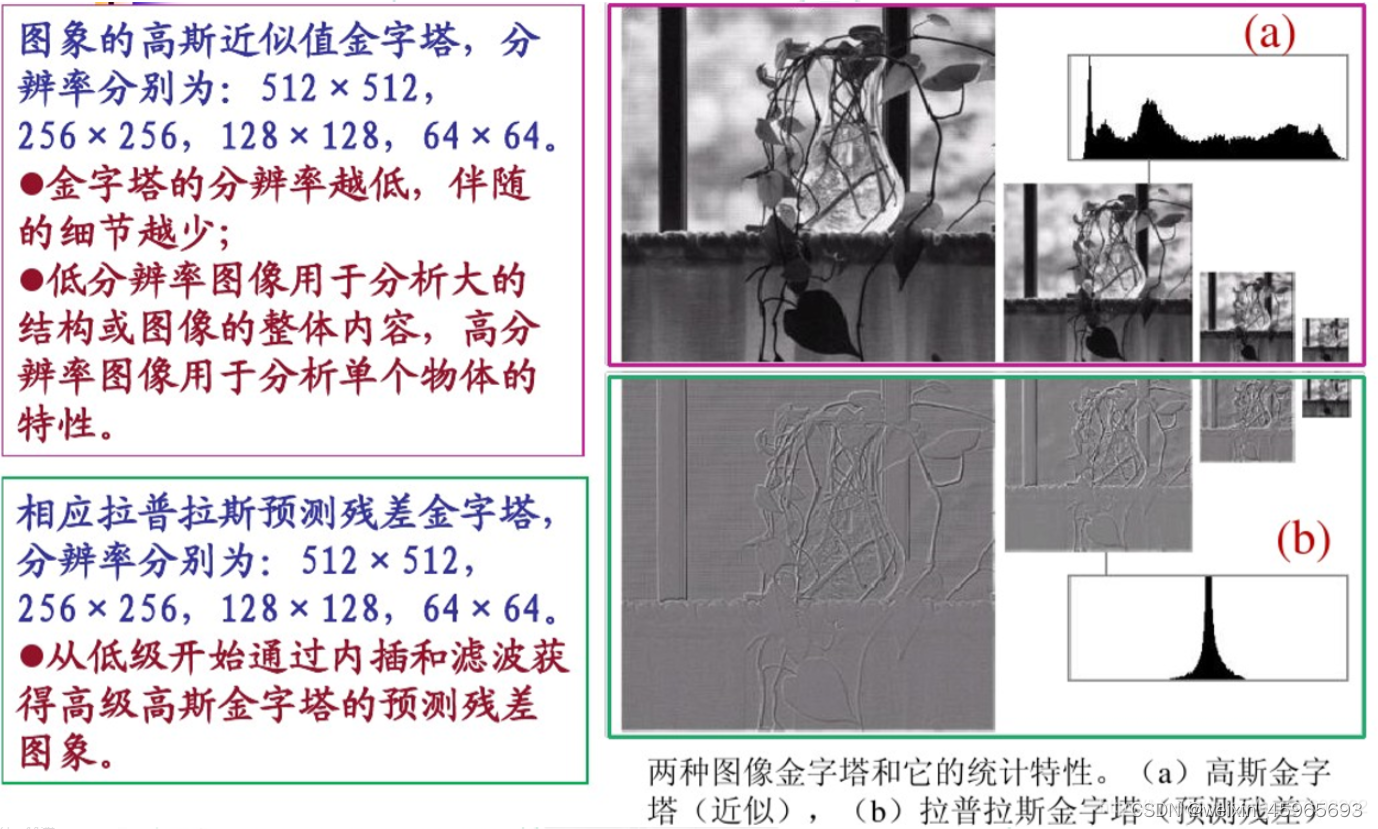
图像金字塔：
为什么要多分辨率处理？一幅自然图像及其直方图的局部变化，不同区域的细节程度不同。

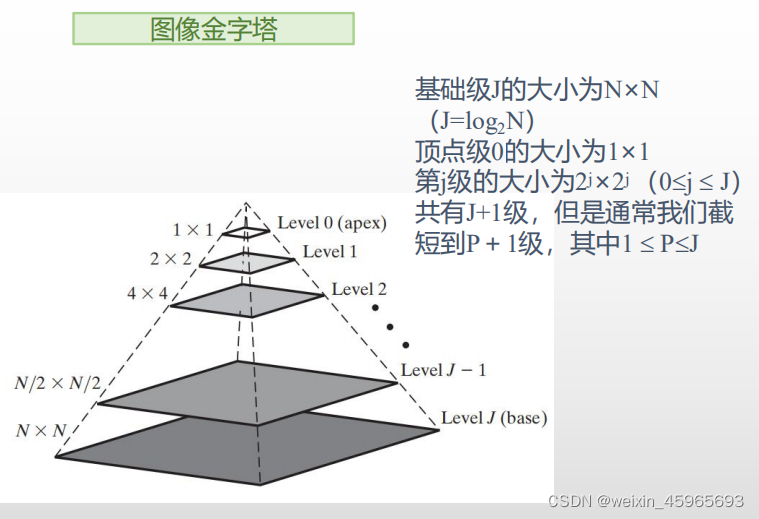
图像金字塔是图像多尺度表达的一种，是一种以多分辨率来解释图像的有效但概念简单的结构。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。
有两种类型的金字塔经常出现在文献和应用当中：
高斯金字塔(Gaussian pyramid): 用来向下采样（主要）
拉普拉斯金字塔(Laplacian pyramid): 用来从金字塔低层图像重建上层未采样图像，可以对图像进行最大程度的还原，配合高斯金字塔一起使用。

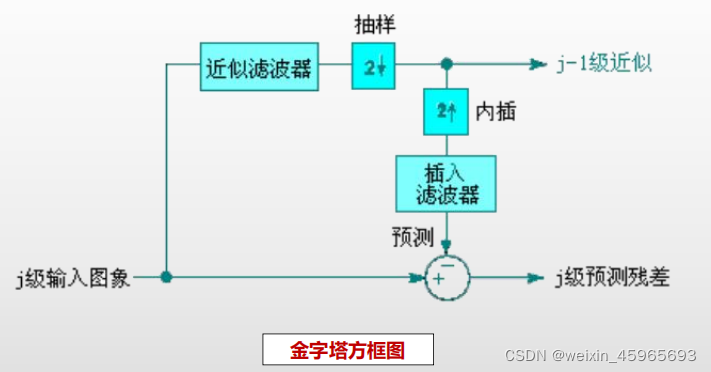
在这里插入图片描述