卷积神经网络基础
一、互相关运算和卷积运算
卷积层是一种误称,因为表达的操作更准确地描述为相互关联。基于对卷积层的描述,在这样的层中,一个输入张量和一个核张量通过一个(互相关操作)组合起来产生一个输出张量。现在先忽略通道,看看它是如何处理二维数据和隐藏表示的。对输入是一个高度为3,宽度为3的二维张量。将张量的形状标记为3×3或(3,3)。核的高和宽都是2。内核窗口(或卷积窗口)的形状由内核的高度和宽度给出(这里是2×2)。
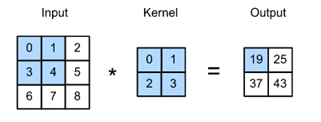
在二维互相关操作中,从位于输入张量左上角的卷积窗口开始,并将其从左到右和从上到下滑动到输入张量。当卷积窗口滑动到某一位置时,将该窗口中包含的输入子张量与核张量进行元素相乘,并将得到的张量相加,得到一个单标量值。这个结果给出了输出张量在相应位置的值。这里输出张量的高度为2,宽度为2。
二、经典边缘检测算子
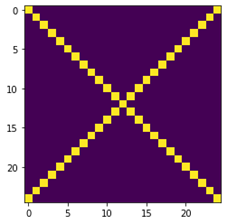
对于对角线检测问题,通过Sobel算子、Roberts算子、Prewitt算子三个一阶检测算子和Laplace算子一个二阶检测算子分别计算得到检测结果,并分别将四个算子所得到的结果作为标签,以此训练网络学习到适合边缘检测的算子。如图2所示,在三个一阶算子中Roberts算子的检测结果最符合预期效果,因此,将其结果作为Y值训练神经网络,预期学习到适用于边缘检测的卷积核。由于Sobel算子的计算原理是由两个卷积核对图像进行卷积运算后得到绝对值相加。为模仿该过程,设置两个卷积核和激活函数来尽可能逼近Sobel算子运算。
而Laplace算子则直接设置一个3*3的卷积核来学习。
检测结果展示:
三、卷积神经网络训练
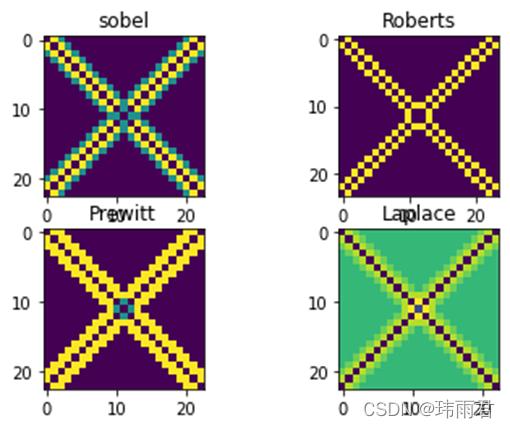
针对Sobel算子中的绝对值运算,分别通过relu、sigmoid、tanh三个非线性激活函数模拟。实验证明,在同样的测试条件下(lr=3e-3,epochs=50,激活函数相同),每次学习得到的结果差距很大。如图3:
而sigoid激活函数学习得到的结果需要取反后才是需要的结果。但是其结果相较于relu做激活函数更稳定。
relu激活下的不同检测效果
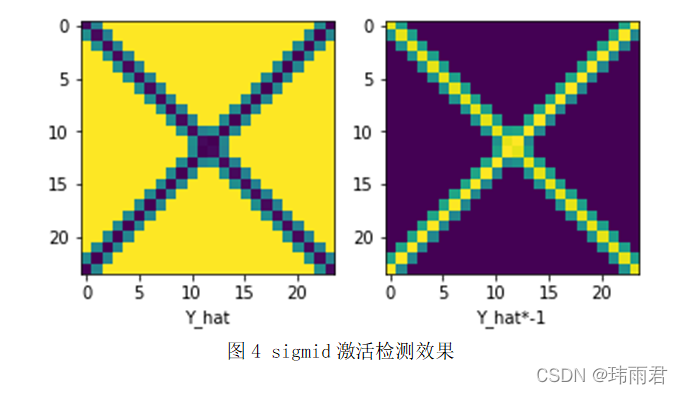
sigmid激活检测效果
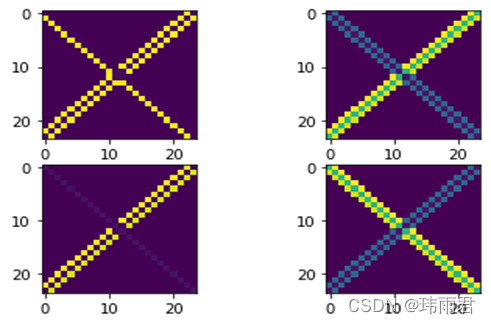
而tanh激活函数下,学习结果更符合预期,通过tanh激活学习得到的检测效果比relu更加稳定,且检测效果更好。虽然tanh激活下的检测效果不如sigmoid稳定,但tanh激活下学习到的卷积核可以直接与图像卷积得到检测结果,无需进行取反操作。
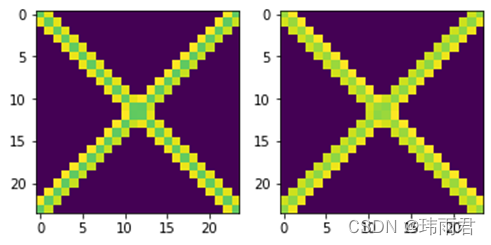
tanh激活检测效果
最后,通过以Laplace算子的检测结果作为Y值。结果卷积神经网络很容易学习到与Laplace算子相似的卷积核。
tensor([[[[ 0.9947, 0.9619, 0.9947],
[ 1.0381, -7.9861, 1.0381],
[ 0.9947, 0.9619, 0.9947]]]])
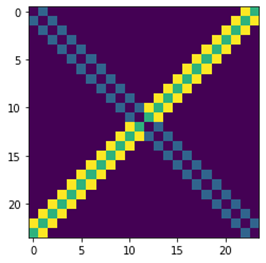
卷积网络学习Laplace算子检测结果