开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> P3P相机姿态估计数学推导求解及自定义实现 -> 正文阅读

[人工智能]P3P相机姿态估计数学推导求解及自定义实现

P3P相机姿态估计数学推导,求解及自定义实现

微信公众号：幼儿园的学霸

前言

PnP问题(Perspective N Points)是指已知3D点的空间坐标及其在相机上的投影,求相机姿态的问题.
投影方程可以表示为:
$\lambda\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=K\left[\begin{array}{ll} R & t \end{array}\right]\left[\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}\right]$
这里的K为相机内参矩阵，是已知的。我们要做的就是从n对这样的对应关系中恢复出相机姿态。

P3P方法是众多解决PnP问题中的一种方案，是通过已知的3对精准匹配的2D-3D点求解图像间相对的位姿变换的一种方法，所用到的信息较少。我们首先需要知道的是P3P并不是直接根据2D-3D点求出相机位姿矩阵，而是先求出对应的2D点在当前相机坐标系下的3D坐标，然后根据世界坐标系下的3D坐标和当前相机坐标系下的3D坐标求解相机位姿的。

下面对具体的求解过程进行推导,包含原理分析及数学公式求解推导,最后利用推导的过程,编写代码自定义实现P3P问题求解,并和OpenCV源码结果进行对比.

首先,设相机坐标中心为点 $O$ ， $X_1,X_2,X_3$ 为空间中不共线的三个3D点,其在图像上对应的投影点为 $x_1,x_2,x_3$ ，如下图所示:
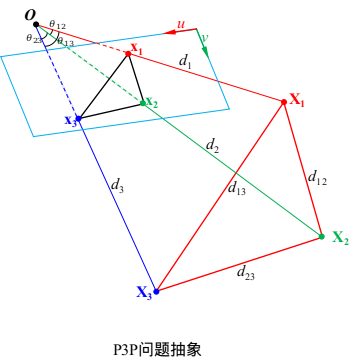
P3P问题抽象
记
$\begin{aligned} |\overrightarrow{OX_i}| &= d_i \\ |\overrightarrow{X_iX_j}| &= d_{ij} \\ \angle X_iOX_j &= \theta_{ij} \quad i,j\in[1,2,3],i\neq j \end{aligned}$

相机到空间点距离求解

对于 $\triangle OX_1X_2$ 如下图所示:
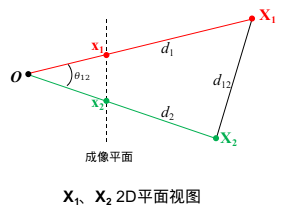
2D投影视图

根据余弦定理可得：
${d_1^2+d_2^2-2d_1d_2cos\theta_{12}= d_{12}^2} \quad \text{(1)}$
同理,对于 $\triangle OX_2X_3 \quad \triangle OX_2X_3$ 也有上述公式成立, 即:
${d_i^2+d_j^2-2d_i d_j cos\theta_{ij}= d_{ij}^2} \quad \text{(2)}$

因此根据余弦定理可以得到如下公式组:
$\begin{aligned} d_1^2+d_2^2-2d_1 d_2 cos\theta_{12} &= d_{12}^2 &\quad\text{(3a)}\\ d_2^2+d_3^2-2d_2 d_3 cos\theta_{23} &= d_{23}^2 &\quad\text{(3b)}\\ d_1^2+d_3^2-2d_1 d_3 cos\theta_{13} &= d_{13}^2 &\quad\text{(3c)} \end{aligned}$

设 $x=\frac{d2}{d1},y=\frac{d3}{d1}$ ,那么:
$\begin{aligned} d_1^2+x^2d_1^2-2d_1^2 x cos\theta_{12} &= d_{12}^2 &\quad\text{(4a)}\\ x^2 d_1^2+y^2 d_1^2-2d_1^2 xy cos\theta_{23} &= d_{23}^2 &\quad\text{(4b)}\\ d_1^2+y^2d_1^2-2d_1^2 y cos\theta_{13} &= d_{13}^2 &\quad\text{(4c)} \end{aligned}$

整理公式(4a)(4b)及(4c)(4b),消元 $d_1^2$ 得:
$\begin{aligned} d_{23}^2 (1+x^2-2x cos\theta_{12} ) &= d_{12}^2(x^2+y^2-2xy cos\theta_{23}) &\quad\text{(5a)}\\ d_{23}^2(1+y^2-2y cos\theta_{13}) &= d_{13}^2 (x^2+y^2-2xy cos\theta_{23}) &\quad\text{(5b)} \end{aligned}$
注意,在上面公式(4)中隐含的条件:
$\begin{aligned} 1+x^2-2x cos\theta_{12} &\neq 0 &\quad \text{(6a)}\\ 1+y^2-2y cos\theta_{13} &\neq 0 &\quad \text{(6b)} \\ x^2+y^2-2xy cos\theta_{23} &\neq 0&\quad \text{(6c)} \end{aligned}$
设 $K_1=(\frac{d_{23}}{d_{13}})^2,K_2=(\frac{d_{23}}{d_{12}})^2$ ,整理上式:
$\begin{aligned} (1-K_{1}) &y^{2}+2(K_{1} cos\theta_{13}-x cos\theta_{23}) y + (x^{2}-K_{1}) &= 0 &\quad \text{(7a)} \\ &y^{2}+2(-x cos\theta_{23}) y + \left[x^{2}(1-K_{2})+2 x K_{2} cos\theta_{12}-K_{2}\right] &= 0 &\quad \text{(7b)} \end{aligned}$
记:
$\begin{aligned} &m = 1-K_1 , p = 2(K_{1} cos\theta_{13}-x cos\theta_{23}) , q = x^{2}-K_{1} \\ &m^{\prime} = 1 , p^{\prime} = 2(-x cos\theta_{23}) , q^{\prime} = \left[x^{2}(1-K_{2})+2 x K_{2} cos\theta_{12}-K_{2}\right] \end{aligned}$
显然, $m,p,q,m^{\prime},p^{\prime},q^{\prime}$ 是关于 $x$ 的多项式
通过变量等效置换,方程组(7)可以写为如下形式:
$\begin{aligned} &0=m y^{2}+p y+q &\quad \text{(8a)} \\ &0=m^{\prime} y^{2}+p^{\prime} y+q^{\prime} &\quad \text{(8b)} \end{aligned}$
对(8a)(8b)按照下面规则进行整理:
$\begin{aligned} m^{\prime}*(8a)-m*(8b) & \quad \text{(9a)} \\ (q^{\prime}*(8a)-q*(8b)) /y &\quad \text{(9b)} \end{aligned}$
得:
$\begin{aligned} (p m^{\prime}-p^{\prime} m) y+(m^{\prime} q-m q^{\prime}) &=0 & \quad \text{(10a)}\\ (m^{\prime} q-m q^{\prime}) y+(p^{\prime} q-p q^{\prime}) &= 0 & \quad \text{(10b)} \end{aligned}$
对 $y$ 进行消元,

隐藏假设 $m^{\prime}q \neq mq{\prime}$

$(m^{\prime}q-mq^{\prime})^2 - (pm^{\prime}-p^{\prime}m)(p^{\prime}q-pq^{\prime}) = 0 \quad \text{(11)}$
对上式进行整理,整理为关于 $x$ 的多项式,可得:
$G_4x^4 +G_3x^3 + G_2x^2 + G_1x + G_0 = 0 \quad \text{(12)}$
其中:
$\begin{aligned} G_{4} &=(K_{1} K_{2}-K_{1}-K_{2})^{2} \\ &-4 K_{1} K_{2} cos^{2}\theta_{23} \\ G_{3} &=4\left(K_{1} K_{2}-K_{1}-K_{2}\right) K_{2}\left(1-K_{1}\right) cos\theta_{12} \\ &+4 K_{1} cos\theta_{23}\left[\left(K_{1} K_{2}-K_{1}+K_{2}\right) cos\theta_{13}+2 K_{2} cos\theta_{12} cos\theta_{23}\right] \\ G_{2} &=\left[2 K_{2}\left(1-K_{1}\right) cos\theta_{12}\right]^{2} \\ &+2\left(K_{1} K_{2}-K_{1}-K_{2}\right)\left(K_{1} K_{2}+K_{1}-K_{2}\right) \\ &+4 K_{1}\left[\left(K_{1}-K_{2}\right) cos^{2}\theta_{23}+K_{1}\left(1-K_{2}\right) cos^{2}\theta_{13}-2\left(1+K_{1}\right) K_{2} cos\theta_{12} cos\theta_{13} cos\theta_{23}\right] \\ G_{1} &=4\left(K_{1} K_{2}+K_{1}-K_{2}\right) K_{2}\left(1-K_{1}\right) cos\theta_{12} \\ &+4 K_{1}\left[\left(K_{1} K_{2}-K_{1}+K_{2}\right) cos\theta_{13} cos\theta_{23}+2 K_{1} K_{2} cos\theta_{12} cos^{2}\theta_{13}\right] \\ G_{0} &=\left(K_{1} K_{2}+K_{1}-K_{2}\right)^{2} \\ &-4 K_{1}^{2} K_{2} cos^{2}\theta_{13} \end{aligned} \quad \text{(13)}$
在系数 $G_i,i=1,2,3,4$ 中,包含的角度 $cos\theta_{12},cos\theta_{23},cos\theta_{13}$ 是能够根据相机内参求得的,后面在展开说明.

多项式系数的展开,化简,可以利用matlab进行推导,代码附后

因此式(12)为一个一元四次方程,是可解的,其有4个解.其求解方法我个人看到的有两种方法:

Ferrari method（费拉里法）
companion matrix method(伴随矩阵法:使用多项式的伴随矩阵进行求解)

相对来说,伴随矩阵法能够基于Eigen库进行快速求解,代码量比较少.OpenCV P3P源码中的四次方程求解实现采用的是http://mathworld.wolfram.com/QuarticEquation.html 所述的方法

同理,根据式(10a),可以求得 $y$ 的表达式,
$H_1y + H_0 = 0 \quad \text{(14)}$
其中:
$\begin{aligned} H_1 &= 2K1*(cos\theta_{13}- xcos\theta_{23}) \\ H_0 &= x^2 - K_1 \\ &- (K_1 - 1) \left[x^2(K_2 - 1) - 2 K_2 xcos\theta_{12} + K_2\right] \end{aligned} \quad \text{(15)}$

根据式(12)求出 $x$ ,然后根据式(14)求出 $y$ ,然后根据式(4a)求出 $d_1$ .由 $x,y,d_1$ 的值可得 $d_2,d_3$ .从而得到相机光心到三个点的距离.但是我们需要的是3个点在相机坐标系下的坐标,而不是具体的长度值,所以还需要根据长度求解点的坐标.

接下来对上面问题继续求解.

角度θ的计算

求解角度之前,回顾一点基础知识,以从相机模型和坐标系谈起.

针孔相机模型如下图所示:

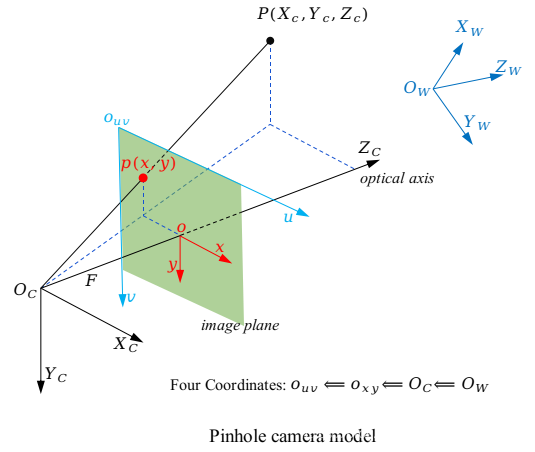
上图中展示了四个坐标系:世界坐标系,相机坐标系,图像平面坐标系,像素坐标系.坐标系的单位依次为: $O_W:mm,O_C:mm,o_{xy}:mm,o_{uv}:pixel$

光心(或者说焦心) $O_C$ 到图像平面的距离为焦距(相机的物理焦距),其单位为mm,图中用大写字母F代替,而避免了常见文章中的小写字母f的样式,这是是为了避免和后面提到的fx,fy混淆. 注意为焦距,而非像距.

其中,像素坐标系和图像平面坐标系的关系如下图所示:
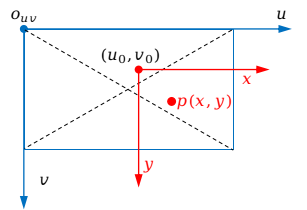
像素坐标系和图像平面坐标系关系

图像平面坐标系中的一个点(unit:mm)转换到像素坐标系下(unit:pixel),其公式如下:
$\left\{\begin{array}{l} u=\frac{x}{d x}+u_{0} \\ v=\frac{y}{d y}+v_{0} \end{array}\right.$

其中:
$d x$ 和 $d y$ 分别表示传感器u轴和v轴上单位像素的实际长度(unit:mm/pixel).对于特定的相机,其CCD尺寸和像素大小是一定的,假设CCD整体尺寸为4.7mm x 3.5mm,分辨率为640x480,那么dx=4.7mm/640pixel=7.4μm/pixel,dy=3.5mm/480pixel=7.4μm/pixel.现代技术下一般二者相等.
$u_0,v_0$ 则表示的是光学中心(Principal Point)，即相机光轴与图像平面的交点，它表征了相机光轴在像素坐标系中的偏移量,以像素为单位.理想情况下其位于图像中心处，此时其值为分辨率的一半.

将上面公式写为矩阵形式:

$\left[\begin{matrix} u \\ v \\ 1 \end{matrix}\right]= \left[\begin{array}{ccc} \frac{1}{d x} & 0 & u_{0} \\ 0 & \frac{1}{d y} & v_{0} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] \quad \text{(20)}$

上面公式实现了物理世界下mm到图像pixel的转换,是图像物理坐标系与像素坐标系转换的关键.

根据相似三角形原理,可得相机坐标系到图像坐标系的转换关系:
$\begin{cases} \frac { x } { F } = \frac { X _ { C } } { Z _ { C } } \\ \frac { y } { F } = \frac { Y _ { C } } { Z _ { C } } \end{cases} \Rightarrow \begin{cases} Z_{C} \cdot x=F \cdot X_{C} \\ Z_{C} \cdot y=F \cdot Y_{C} \end{cases}$
同样,写为矩阵形式:
$Z_C \left[\begin{matrix} x \\ y \\ 1 \end{matrix}\right]= \left[\begin{matrix} F & 0 & 0 & 0 \\ 0 & F & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix}\right] \left[\begin{matrix} X_C \\ Y_C \\ Z_C \\ 1 \end{matrix}\right] \quad \text{(21)}$
相机坐标系上的点投影到成像平面上之后，此时在成像平面上的单位还依旧是长度单位.

后面还有世界坐标系到相机坐标系的转换,其为刚体变换,相关资料已很多,此处不在赘述.

将公式(20)(21)整理可得相机坐标系到像素坐标系的转换关系:
$\begin{aligned} Z_C \left[\begin{matrix} u \\ v \\ 1 \end{matrix}\right] & = \left[\begin{matrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} F & 0 & 0 & 0 \\ 0 & F & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix}\right] \left[\begin{matrix} X_C \\ Y_C \\ Z_C \\ 1 \end{matrix}\right] \\ &= \left[\begin{matrix} \frac{F}{dx} & 0 & u_0 & 0 \\ 0 & \frac{F}{dy} & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix}\right] \left[\begin{matrix} X_C \\ Y_C \\ Z_C \\ 1 \end{matrix}\right] \\ &= \left[\begin{matrix} f_x & 0 & u_0 & 0 \\ 0 & f_y & v_0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix}\right] \left[\begin{matrix} X_C \\ Y_C \\ Z_C \\ 1 \end{matrix}\right] \end{aligned} \quad \text{(22)}$
其中 $f_x ＝ F/dx ,f_y = F/dy$ ,分别称为u轴和v轴上的归一化焦距

这就是OpenCV中相机的内参 $f_x,f_y$

从公式(22)可以看到,若一个点的 $Z_C,u,v$ 坐标已知,则可以求出其在相机坐标系下的坐标.

根据向量内积公式,由:
$\vec a * \vec b = |\vec a|*|\vec b|*cos<\vec a,\vec b>$
所以,
$\begin{aligned} cons \theta_{ij} &= \frac{\overrightarrow {OX_i}*\overrightarrow {OX_j} }{|\overrightarrow {OX_i}|*|\overrightarrow {OX_j}|} \\ &= \frac{\overrightarrow {OX_i}}{|\overrightarrow {OX_i}|} * \frac{\overrightarrow {OX_j}}{|\overrightarrow {OX_j}|} \end{aligned} \quad \text{(23)}$
即:两条边之间的夹角余弦值为两条边方向向量(单位向量)的内积.

在相机坐标系下,点O的坐标为 $(0, 0, 0)$ ,但是 $X_i$ 的 $Z_C$ 坐标未知.因此,直接求解上述公式存在一定困难.

但是,仔细观察上面相机针孔模型示意图,我们可以将图像平面坐标系看做相机坐标系下 $Z_c=F$ 的一个平面,进而将上面的点都视为相机坐标系的一部分.那么点 $x_i$ 的 $Z_C$ 坐标是已知的,进而可得其在相机坐标系下的另外两个维度的坐标.

因此,可以将公式(23)写为如下形式来求解余弦值:
$\begin{aligned} cons \theta_{ij} &= \frac{\overrightarrow {Ox_i}*\overrightarrow {Ox_j} }{|\overrightarrow {Ox_i}|*|\overrightarrow {Ox_j}|} \end{aligned} \quad \text{(24)}$
根据公式(22)及 $x_i$ 的 $Z_C=F$ ,可得 $x_i$ 在相机坐标系下的坐标为:
$\overrightarrow {Ox_i} = \begin{aligned} (F*\frac{u_i-u_0}{f_x},F*\frac{v_i-v_0}{f_y},F) \end{aligned} \quad \text{(25)}$
一般我们会将Z坐标归一化为1,即求解 $Z_C=1$ 平面上点的坐标,或者说,求解其在归一化图像平面上的坐标,此时根据公式(22)可知点在归一化图像平面上的坐标为:
$\overrightarrow {Ox_i}|_{Z_C=1} = \begin{aligned} (\frac{u_i-u_0}{f_x},\frac{v_i-v_0}{f_y},1) \end{aligned} \quad \text{(26)}$

公式(25)(26)的单位和相机坐标系的单位一致,均为mm.
同样将将公式(26)写为矩阵形式如下:
$\begin{aligned} {X_i}|_{Z_C=1} = \left[\begin{matrix} \frac{u_i-u_0}{f_x} \\ \frac{v_i-v_0}{f_y} \\ 1 \end{matrix}\right] & = \left[\begin{matrix} \frac{1}{f_x} & 0 & -\frac{u_0}{f_x}\\ 0 & \frac{1}{f_y} & -\frac{v_0}{f_y}\\ 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} u_i \\ v_i \\ 1 \end{matrix}\right] \\ &= \left[\begin{matrix} {f_x} & 0 & {u_0}\\ 0 & {f_y} & {v_0}\\ 0 & 0 & 1 \end{matrix}\right]^{-1} \left[\begin{matrix} u_i \\ v_i \\ 1 \end{matrix}\right] \\ &= \mathrm{K}^{-1} \left[\begin{matrix} u_i \\ v_i \\ 1 \end{matrix}\right] \end{aligned} \quad \text{(26b)}$
根据公式(26)可以求出 $\overrightarrow Ox_i$ 的方向向量,接着可以对其进行L2归一化,使其模长为1,变为单位向量(单位坐标).
$normlized(\overrightarrow {OX_i}) = \frac{\overrightarrow {Ox_i}|_{Z_C=1}}{|\overrightarrow {Ox_i}|_{Z_C=1}|} \quad \text{(27)}$
由公式(27)或(26)结合公式(24)可解3个角度的余弦值.

扩展
更一般的,根据浙江大学谭平老师的课堂内容, 求解任意两点与相机光心连线夹角余弦值,写为矩阵形式,有下列形式:
$\begin{aligned} cos \theta &=\frac{\mathrm{X}_{1}^{T} X_{2}}{\sqrt{\left(\mathrm{X}_{1}^{T} \mathrm{X}_{1}\right)\left(\mathrm{X}_{2}^{T} \mathrm{X}_{2}\right)}} \\ &=\frac{\mathrm{x}_{1}^{\mathrm{T}}\left(\mathrm{K}^{-\mathrm{T}} \mathrm{K}^{-1}\right) \mathrm{x}_{2}}{\sqrt{\left(\mathrm{x}_{1}^{T}\left(\mathrm{K}^{-T} \mathrm{K}^{-1}\right) \mathrm{x}_{1}\right)\left(\mathrm{x}_{2}^{T}\left(\mathrm{K}^{-T} \mathrm{K}^{-1}\right) \mathrm{x}_{2}\right)}} \end{aligned} \quad \text{(28)}$
其中: $K,K^{-1},K^{-T}$ 为相机内参矩阵,内参矩阵的逆,内参矩阵转置的逆;而 $K^{-1}$ 表征了相机坐标系下光线(相机中心连接像素点)的方向;
$X_1,X_2$ 为点在相机坐标系下的坐标(由于其Z坐标为1,故或者说归一化图像平面上的坐标),为3x1矩阵形式,单位为mm;
$x_1,x_2$ 为点在像素坐标系下的坐标,为3x1矩阵形式 $\left[\begin{array}{l} u & v &1 \end{array}\right]^T$ ,单位为pixel.

在公式(28)两个等号之间的转换过程中,用了下面的转换关系:
$\begin{aligned} & \mathrm{x} = \mathrm{K} \left[\begin{array}{c|c} \mathrm{I} & \mathrm{0} \end{array}\right] \left[\begin{array}{l} \mathrm{X} \\ 0 \end{array}\right] \quad \text{(29a)} \\ & \Longrightarrow \mathrm{X}= \mathrm{K}^{-1}\mathrm{x} \quad \text{(29b)} \end{aligned}$
公式(29a)可以这样理解:相机坐标系下,内参矩阵还是 $K$ ,外参矩阵变为了 $\left[\begin{array}{c|c} \mathrm{I} & \mathrm{0} \end{array}\right]$ ,即旋转矩阵变成了单位矩阵,平移向量是0.
另外,可以看到公式(29b)的结果和上面(26b)整理的结果是一样的.

公式(28)表明,如果知道了相机内参矩阵,就可以求得图像中任意两个点关于相机中心的夹角.
利用内参求解夹角

该部分感兴趣的可以搜索了解.或者可以写代码验证公式(28)的结果和(24)的结果是相同的;利用公式(29b)求得的结果和公式(26)的结果是相同的.

相机坐标系下的坐标计算

接下来求解3个点在相机坐标系下的坐标. 该部分比较简单,在上面部分中,求解得到了光心到3个点的距离,以及光心到3个点的方向向量(单位向量形式)(公式(27)).我们直接利用向量公式即可求出点在相机坐标系下的坐标,公式如下:
$\begin{aligned} \overrightarrow {OX_i} = normlized(\overrightarrow {OX_i}) * |OX_i| \quad \text{(30)} \end{aligned}$

求得点在相机坐标系下的坐标之后,在根据点在世界坐标系下的坐标,就能求出相机的外参(相机坐标系到世界坐标系的转换矩阵).一般情况下得到了4组解(结合实际的成像模型,应该可以缩减为2个解,这两个解行成的平面正好朝向相反),可以额外加一个点来进行辅助选择,确认哪组解的误差最小,从而求出唯一解.

自定义实现

OpenCV源码中p3p算法采用的是高小山的论文:Complete Solution Classification for the Perspective-Three-Point Problem

根据上面的推导过程,以及具体的数学解,基于OpenCV的实现框架,自定义实现P3P的求解.
并和OpenCV自带结果进行对比.
代码如下,具体流程可以参考代码注释进行理解.

p3p封装为类.外部调用函数保持和OpenCV一致.
头文件:p3p.h

//
// Created by liheng on 10/2/21.
//

//Program:自定义实现P3P算法
//Date:2021-10-2
//Author:liheng
//Version:V1.0
//Note:框架来源于OpenCV源码,但是相机到空间点距离求解部分未采用论文中的消元法
//      修改为自己的推导过程
//====================================================================//

#ifndef OPENCVDEMO_P3P_H
#define OPENCVDEMO_P3P_H


#include <opencv2/opencv.hpp>

class p3p
{
 public:
  p3p(double fx, double fy, double cx, double cy);
  p3p(cv::Mat cameraMatrix);

  bool solve(cv::Mat& R, cv::Mat& tvec, const cv::Mat& opoints, const cv::Mat& ipoints);
  int solve(std::vector<cv::Mat>& Rs, std::vector<cv::Mat>& tvecs, const cv::Mat& opoints, const cv::Mat& ipoints);
  int solve(double R[4][3][3], double t[4][3],
            double mu0, double mv0,   double X0, double Y0, double Z0,
            double mu1, double mv1,   double X1, double Y1, double Z1,
            double mu2, double mv2,   double X2, double Y2, double Z2,
            double mu3, double mv3,   double X3, double Y3, double Z3,
            bool p4p);
  bool solve(double R[3][3], double t[3],
             double mu0, double mv0,   double X0, double Y0, double Z0,
             double mu1, double mv1,   double X1, double Y1, double Z1,
             double mu2, double mv2,   double X2, double Y2, double Z2,
             double mu3, double mv3,   double X3, double Y3, double Z3);

 private:
  template <typename T>
  void init_camera_parameters(const cv::Mat& cameraMatrix)
  {
    cx = cameraMatrix.at<T> (0, 2);
    cy = cameraMatrix.at<T> (1, 2);
    fx = cameraMatrix.at<T> (0, 0);
    fy = cameraMatrix.at<T> (1, 1);
  }
  template <typename OpointType, typename IpointType>
  void extract_points(const cv::Mat& opoints, const cv::Mat& ipoints, std::vector<double>& points)
  {
      points.clear();
      int npoints = std::max(opoints.checkVector(3, CV_32F), opoints.checkVector(3, CV_64F));
      points.resize(5*4); //resize vector to fit for p4p case
      for(int i = 0; i < npoints; i++)
      {
//          points[i*5] = ipoints.at<IpointType>(i).x*fx + cx;
//          points[i*5+1] = ipoints.at<IpointType>(i).y*fy + cy;
//          points[i*5+2] = opoints.at<OpointType>(i).x;
//          points[i*5+3] = opoints.at<OpointType>(i).y;
//          points[i*5+4] = opoints.at<OpointType>(i).z;

          points[i*5] = ipoints.at<IpointType>(i).x;
          points[i*5+1] = ipoints.at<IpointType>(i).y;
          points[i*5+2] = opoints.at<OpointType>(i).x;
          points[i*5+3] = opoints.at<OpointType>(i).y;
          points[i*5+4] = opoints.at<OpointType>(i).z;
      }
      //Fill vectors with unused values for p3p case
      for (int i = npoints; i < 4; i++) {
          for (int j = 0; j < 5; j++) {
              points[i * 5 + j] = 0;
          }
      }
  }
  void init_inverse_parameters();

  //求解光心到各点的距离
  //Reference : X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang; "Complete Solution Classification for the Perspective-Three-Point Problem"
  int solve_for_lengths(double lengths[4][3], double distances[3], double cosines[3]);

  //求解光心到各点的距离
  //按照公式自己推导过程进行求解
  int my_solve_for_lengths(double lengths[4][3], double distances[3], double cosines[3]);

  bool align(double M_start[3][3],
             double X0, double Y0, double Z0,
             double X1, double Y1, double Z1,
             double X2, double Y2, double Z2,
             double R[3][3], double T[3]);

  bool jacobi_4x4(double * A, double * D, double * U);

  double fx, fy, cx, cy;
  double inv_fx, inv_fy, cx_fx, cy_fy;
};


//多项式求解
//系数按照多项式的幂降序排列
int solve_deg2(double a, double b, double c, double & x1, double & x2);

int solve_deg3(double a, double b, double c, double d,
               double & x0, double & x1, double & x2);

int solve_deg4(double a, double b, double c, double d, double e,
               double & x0, double & x1, double & x2, double & x3);


//封装P3P为函数,保持和OpenCV一致

/** @brief Finds an object pose from 3 3D-2D point correspondences.

@param objectPoints Array of object points in the object coordinate space, 3x3 1-channel or
1x3/3x1 3-channel. vector\<Point3f\> can be also passed here.
@param imagePoints Array of corresponding image points, 3x2 1-channel or 1x3/3x1 2-channel.
 vector\<Point2f\> can be also passed here.
@param cameraMatrix Input camera matrix \f$A = \vecthreethree{f_x}{0}{c_x}{0}{f_y}{c_y}{0}{0}{1}\f$ .
@param distCoeffs Input vector of distortion coefficients
\f$(k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4[, \tau_x, \tau_y]]]])\f$ of
4, 5, 8, 12 or 14 elements. If the vector is NULL/empty, the zero distortion coefficients are
assumed.
@param rvecs Output rotation vectors (see @ref Rodrigues ) that, together with tvecs, brings points from
the model coordinate system to the camera coordinate system. A P3P problem has up to 4 solutions.
@param tvecs Output translation vectors.
@param flags Method for solving a P3P problem:
-   **SOLVEPNP_P3P** Method is based on the paper of X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang
"Complete Solution Classification for the Perspective-Three-Point Problem" (@cite gao2003complete).
-   **SOLVEPNP_AP3P** Method is based on the paper of T. Ke and S. Roumeliotis.
"An Efficient Algebraic Solution to the Perspective-Three-Point Problem" (@cite Ke17).

The function estimates the object pose given 3 object points, their corresponding image
projections, as well as the camera matrix and the distortion coefficients.

@note
The solutions are sorted by reprojection errors (lowest to highest).
 */
int SolveP3P( cv::InputArray objectPoints, cv::InputArray imagePoints,
              cv::InputArray cameraMatrix, cv::InputArray distCoeffs,
              cv::OutputArrayOfArrays rvecs, cv::OutputArrayOfArrays tvecs,
              int flags );

#endif // OPENCVDEMO_P3P_H

实现文件:p3p.cpp

#include <cstring>
#include <cmath>
#include <iostream>

#include "p3p.h"

void p3p::init_inverse_parameters()
{
    inv_fx = 1. / fx;
    inv_fy = 1. / fy;
    cx_fx = cx / fx;
    cy_fy = cy / fy;
}

p3p::p3p(cv::Mat cameraMatrix)
{
    if (cameraMatrix.depth() == CV_32F)
        init_camera_parameters<float>(cameraMatrix);
    else
        init_camera_parameters<double>(cameraMatrix);
    init_inverse_parameters();
}

p3p::p3p(double _fx, double _fy, double _cx, double _cy)
{
    fx = _fx;
    fy = _fy;
    cx = _cx;
    cy = _cy;
    init_inverse_parameters();
}

bool p3p::solve(cv::Mat& R, cv::Mat& tvec, const cv::Mat& opoints, const cv::Mat& ipoints)
{
    double rotation_matrix[3][3] = {}, translation[3] = {};
    std::vector<double> points;
    if (opoints.depth() == ipoints.depth())
    {
        if (opoints.depth() == CV_32F)
            extract_points<cv::Point3f,cv::Point2f>(opoints, ipoints, points);
        else
            extract_points<cv::Point3d,cv::Point2d>(opoints, ipoints, points);
    }
    else if (opoints.depth() == CV_32F)
        extract_points<cv::Point3f,cv::Point2d>(opoints, ipoints, points);
    else
        extract_points<cv::Point3d,cv::Point2f>(opoints, ipoints, points);

    bool result = solve(rotation_matrix, translation,
                        points[0], points[1], points[2], points[3], points[4],
                        points[5], points[6], points[7], points[8], points[9],
                        points[10], points[11], points[12], points[13], points[14],
                        points[15], points[16], points[17], points[18], points[19]);
    cv::Mat(3, 1, CV_64F, translation).copyTo(tvec);
    cv::Mat(3, 3, CV_64F, rotation_matrix).copyTo(R);
    return result;
}

int p3p::solve(std::vector<cv::Mat>& Rs, std::vector<cv::Mat>& tvecs, const cv::Mat& opoints, const cv::Mat& ipoints)
{
    double rotation_matrix[4][3][3] = {}, translation[4][3] = {};
    std::vector<double> points;
    if (opoints.depth() == ipoints.depth())
    {
        if (opoints.depth() == CV_32F)
            extract_points<cv::Point3f,cv::Point2f>(opoints, ipoints, points);
        else
            extract_points<cv::Point3d,cv::Point2d>(opoints, ipoints, points);
    }
    else if (opoints.depth() == CV_32F)
        extract_points<cv::Point3f,cv::Point2d>(opoints, ipoints, points);
    else
        extract_points<cv::Point3d,cv::Point2f>(opoints, ipoints, points);

    const bool p4p = std::max(opoints.checkVector(3, CV_32F), opoints.checkVector(3, CV_64F)) == 4;
    int solutions = solve(rotation_matrix, translation,
                          points[0], points[1], points[2], points[3], points[4],
                          points[5], points[6], points[7], points[8], points[9],
                          points[10], points[11], points[12], points[13], points[14],
                          points[15], points[16], points[17], points[18], points[19],
                          p4p);

    for (int i = 0; i < solutions; i++)
    {
        cv::Mat R, tvec;
        cv::Mat(3, 1, CV_64F, translation[i]).copyTo(tvec);
        cv::Mat(3, 3, CV_64F, rotation_matrix[i]).copyTo(R);

        Rs.push_back(R);
        tvecs.push_back(tvec);
    }

    return solutions;
}

bool p3p::solve(double R[3][3], double t[3],
                double mu0, double mv0,   double X0, double Y0, double Z0,
                double mu1, double mv1,   double X1, double Y1, double Z1,
                double mu2, double mv2,   double X2, double Y2, double Z2,
                double mu3, double mv3,   double X3, double Y3, double Z3)
{
    double Rs[4][3][3] = {}, ts[4][3] = {};

    const bool p4p = true;
    int n = solve(Rs, ts, mu0, mv0, X0, Y0, Z0,  mu1, mv1, X1, Y1, Z1, mu2, mv2, X2, Y2, Z2, mu3, mv3, X3, Y3, Z3, p4p);

    if (n == 0)
        return false;

    for(int i = 0; i < 3; i++) {
        for(int j = 0; j < 3; j++)
            R[i][j] = Rs[0][i][j];
        t[i] = ts[0][i];
    }

    return true;
}

int p3p::solve(double R[4][3][3], double t[4][3],
               double mu0, double mv0,   double X0, double Y0, double Z0,
               double mu1, double mv1,   double X1, double Y1, double Z1,
               double mu2, double mv2,   double X2, double Y2, double Z2,
               double mu3, double mv3,   double X3, double Y3, double Z3,
               bool p4p)
{
    if(0)
    {
        //验证:利用公式(28)的矩阵形式计算余弦
        cv::Mat x1 = (cv::Mat_<double>(3,1) << mu0,mv0,1);
        cv::Mat x2 = (cv::Mat_<double>(3,1) << mu1,mv1,1);

        //内参矩阵
        cv::Mat K = (cv::Mat_<double>(3,3) <<
                fx,0,cx,
                0,fy,cy,
                0,0,1);

        cv::Mat X = K.inv()*x1;//公式29(b)或者说是(26b)
        std::cout<<"lihengXXXX:"<<X<<std::endl;

        cv::Mat H = ( K.t() ).inv()*K.inv();
        cv::Mat numerator = x1.t()*H*x2;//公式(28)的分子部分
        cv::Mat denominator_2 = (x1.t()*H*x1)*(x2.t()*H*x2);//公式(28)的 分母^2 部分

        auto C12 = numerator.at<double>(0,0) / std::sqrt(denominator_2.at<double>(0,0));
        std::cout<<C12<<std::endl;
    }


    double mk0, mk1, mk2;
    double norm;

    //求解归一化图像平面上的坐标--公式(26);
    // 然后单位化--公式(27)
    mu0 = inv_fx * mu0 - cx_fx;
    mv0 = inv_fy * mv0 - cy_fy;//求解归一化图像平面上坐标:Z_C=1的平面
    norm = sqrt(mu0 * mu0 + mv0 * mv0 + 1);//求模长
    mk0 = 1. / norm; mu0 *= mk0; mv0 *= mk0;//转换为单位向量(单位坐标)

    mu1 = inv_fx * mu1 - cx_fx;
    mv1 = inv_fy * mv1 - cy_fy;
    norm = sqrt(mu1 * mu1 + mv1 * mv1 + 1);
    mk1 = 1. / norm; mu1 *= mk1; mv1 *= mk1;

    mu2 = inv_fx * mu2 - cx_fx;
    mv2 = inv_fy * mv2 - cy_fy;
    norm = sqrt(mu2 * mu2 + mv2 * mv2 + 1);
    mk2 = 1. / norm; mu2 *= mk2; mv2 *= mk2;

    mu3 = inv_fx * mu3 - cx_fx;
    mv3 = inv_fy * mv3 - cy_fy;

    double distances[3];
    distances[0] = sqrt( (X1 - X2) * (X1 - X2) + (Y1 - Y2) * (Y1 - Y2) + (Z1 - Z2) * (Z1 - Z2) );//d12
    distances[1] = sqrt( (X0 - X2) * (X0 - X2) + (Y0 - Y2) * (Y0 - Y2) + (Z0 - Z2) * (Z0 - Z2) );//d02
    distances[2] = sqrt( (X0 - X1) * (X0 - X1) + (Y0 - Y1) * (Y0 - Y1) + (Z0 - Z1) * (Z0 - Z1) );//d01

    // Calculate angles
    //公式(24) 向量内积,计算角度
    double cosines[3];
    cosines[0] = mu1 * mu2 + mv1 * mv2 + mk1 * mk2;//C12
    cosines[1] = mu0 * mu2 + mv0 * mv2 + mk0 * mk2;//C02
    cosines[2] = mu0 * mu1 + mv0 * mv1 + mk0 * mk1;//C01

    double lengths[4][3] = {};
    int n = my_solve_for_lengths(lengths, distances, cosines);//自己推导实现的长度计算
    //n = solve_for_lengths(lengths, distances, cosines);//OpenCV源码中长度计算




    //利用公式(30) 计算点在相机坐标系下的坐标
    int nb_solutions = 0;
    double reproj_errors[4];
    for(int i = 0; i < n; i++)
    {
        double M_orig[3][3];

        M_orig[0][0] = lengths[i][0] * mu0;
        M_orig[0][1] = lengths[i][0] * mv0;
        M_orig[0][2] = lengths[i][0] * mk0;

        M_orig[1][0] = lengths[i][1] * mu1;
        M_orig[1][1] = lengths[i][1] * mv1;
        M_orig[1][2] = lengths[i][1] * mk1;

        M_orig[2][0] = lengths[i][2] * mu2;
        M_orig[2][1] = lengths[i][2] * mv2;
        M_orig[2][2] = lengths[i][2] * mk2;

        //ICP 求解外参矩阵
        if (!align(M_orig, X0, Y0, Z0, X1, Y1, Z1, X2, Y2, Z2, R[nb_solutions], t[nb_solutions]))
            continue;

        //利用第4个点辅助选择
        if (p4p)
        {
            double X3p = R[nb_solutions][0][0] * X3 + R[nb_solutions][0][1] * Y3 + R[nb_solutions][0][2] * Z3 + t[nb_solutions][0];
            double Y3p = R[nb_solutions][1][0] * X3 + R[nb_solutions][1][1] * Y3 + R[nb_solutions][1][2] * Z3 + t[nb_solutions][1];
            double Z3p = R[nb_solutions][2][0] * X3 + R[nb_solutions][2][1] * Y3 + R[nb_solutions][2][2] * Z3 + t[nb_solutions][2];
            double mu3p = X3p / Z3p;
            double mv3p = Y3p / Z3p;
            reproj_errors[nb_solutions] = (mu3p - mu3) * (mu3p - mu3) + (mv3p - mv3) * (mv3p - mv3);
        }

        nb_solutions++;
    }

    if (p4p)
    {
        //sort the solutions
        for (int i = 1; i < nb_solutions; i++)
        {
            for (int j = i; j > 0 && reproj_errors[j-1] > reproj_errors[j]; j--)
            {
                std::swap(reproj_errors[j], reproj_errors[j-1]);
                std::swap(R[j], R[j-1]);
                std::swap(t[j], t[j-1]);
            }
        }
    }

    return nb_solutions;
}

/// Given 3D distances between three points and cosines of 3 angles at the apex, calculates
/// the lengths of the line segments connecting projection center (P) and the three 3D points (A, B, C).
/// Returned distances are for |PA|, |PB|, |PC| respectively.
/// Only the solution to the main branch.
/// Reference : X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang; "Complete Solution Classification for the Perspective-Three-Point Problem"
/// IEEE Trans. on PAMI, vol. 25, No. 8, August 2003
/// \param lengths3D Lengths of line segments up to four solutions.
/// \param dist3D Distance between 3D points in pairs |BC|, |AC|, |AB|.
/// \param cosines Cosine of the angles /_BPC, /_APC, /_APB.
/// \returns Number of solutions.
/// WARNING: NOT ALL THE DEGENERATE CASES ARE IMPLEMENTED

int p3p::solve_for_lengths(double lengths[4][3], double distances[3], double cosines[3])
{
    double p = cosines[0] * 2;
    double q = cosines[1] * 2;
    double r = cosines[2] * 2;

    double inv_d22 = 1. / (distances[2] * distances[2]);
    double a = inv_d22 * (distances[0] * distances[0]);
    double b = inv_d22 * (distances[1] * distances[1]);

    double a2 = a * a, b2 = b * b, p2 = p * p, q2 = q * q, r2 = r * r;
    double pr = p * r, pqr = q * pr;

    // Check reality condition (the four points should not be coplanar)
    if (p2 + q2 + r2 - pqr - 1 == 0)
        return 0;

    double ab = a * b, a_2 = 2*a;

    double A = -2 * b + b2 + a2 + 1 + ab*(2 - r2) - a_2;

    // Check reality condition
    if (A == 0) return 0;

    double a_4 = 4*a;

    double B = q*(-2*(ab + a2 + 1 - b) + r2*ab + a_4) + pr*(b - b2 + ab);
    double C = q2 + b2*(r2 + p2 - 2) - b*(p2 + pqr) - ab*(r2 + pqr) + (a2 - a_2)*(2 + q2) + 2;
    double D = pr*(ab-b2+b) + q*((p2-2)*b + 2 * (ab - a2) + a_4 - 2);
    double E = 1 + 2*(b - a - ab) + b2 - b*p2 + a2;

    double temp = (p2*(a-1+b) + r2*(a-1-b) + pqr - a*pqr);
    double b0 = b * temp * temp;
    // Check reality condition
    if (b0 == 0)
        return 0;

    double real_roots[4];
    int n = solve_deg4(A, B, C, D, E,  real_roots[0], real_roots[1], real_roots[2], real_roots[3]);

    if (n == 0)
        return 0;

    int nb_solutions = 0;
    double r3 = r2*r, pr2 = p*r2, r3q = r3 * q;
    double inv_b0 = 1. / b0;

    // For each solution of x
    for(int i = 0; i < n; i++) {
        double x = real_roots[i];

        // Check reality condition
        if (x <= 0)
            continue;

        double x2 = x*x;

        double b1 =
                ((1-a-b)*x2 + (q*a-q)*x + 1 - a + b) *
                (((r3*(a2 + ab*(2 - r2) - a_2 + b2 - 2*b + 1)) * x +

                  (r3q*(2*(b-a2) + a_4 + ab*(r2 - 2) - 2) + pr2*(1 + a2 + 2*(ab-a-b) + r2*(b - b2) + b2))) * x2 +

                 (r3*(q2*(1-2*a+a2) + r2*(b2-ab) - a_4 + 2*(a2 - b2) + 2) + r*p2*(b2 + 2*(ab - b - a) + 1 + a2) + pr2*q*(a_4 + 2*(b - ab - a2) - 2 - r2*b)) * x +

                 2*r3q*(a_2 - b - a2 + ab - 1) + pr2*(q2 - a_4 + 2*(a2 - b2) + r2*b + q2*(a2 - a_2) + 2) +
                 p2*(p*(2*(ab - a - b) + a2 + b2 + 1) + 2*q*r*(b + a_2 - a2 - ab - 1)));

        // Check reality condition
        if (b1 <= 0)
            continue;

        double y = inv_b0 * b1;
        double v = x2 + y*y - x*y*r;

        if (v <= 0)
            continue;

        double Z = distances[2] / sqrt(v);
        double X = x * Z;
        double Y = y * Z;

        lengths[nb_solutions][0] = X;
        lengths[nb_solutions][1] = Y;
        lengths[nb_solutions][2] = Z;

        nb_solutions++;
    }

    return nb_solutions;
}

int p3p::my_solve_for_lengths(double lengths[4][3], double distances[3], double cosines[3])
{
    //传进来的数据的下标顺序为12 02 01
    //对应推导公式中的23 13 12

    //0 1 2
    const auto d23 = distances[0];
    const auto d13 = distances[1];
    const auto d12 = distances[2];

    const auto C23 = cosines[0];
    const auto C13 = cosines[1];
    const auto C12 = cosines[2];

    const auto C23_2 = C23*C23;
    const auto C13_2 = C13*C13;
    const auto C12_2 = C12*C12;
    const auto C123 = C23 * C13 * C12;

    //判断点是否共面
    //Check reality condition (the four points should not be coplanar)
    if( C23_2 + C13_2 + C12_2 - 2*C123 -1 == 0)//OpenCV p3p源码中该部分可能有误
        return 0;

    //TODO:判断距离是否为0 提前返回
    //求解系数--公式(13)
    const auto K1 = std::pow(d23/d13,2);
    const auto K2 = std::pow(d23/d12,2);

    const auto G4 = std::pow(K1*K2-K1-K2,2) - 4*K1*K2*C23_2;
    // Check reality condition
    if (G4 == 0)
        return 0;

    const auto G3 = 4*(K1*K2-K1-K2)*K2*(1-K1)*C12 +
            4*K1*C23*( (K1*K2-K1+K2)*C13 + 2*K2*C12*C23 );

    const auto G2 = std::pow(2*K2*(1-K1)*C12,2) +
            2*(K1*K2-K1-K2)*(K1*K2+K1-K2) +
            4*K1*((K1-K2)*C23_2 + K1*(1-K2)*C13_2 -2*(1+K1)*K2*C123 );

    const auto G1 = 4*(K1*K2+K1-K2)*K2*(1-K1)*C12 +
            4*K1*((K1*K2-K1+K2)*C13*C23 + 2*K1*K2*C12*C13_2);
    const auto G0 = std::pow(K1*K2+K1-K2,2) - 4*K1*K1*K2*C13_2;

    //求解公式(12)中x的解
    double real_roots[4]={0};
    int n = solve_deg4(G4, G3, G2, G1, G0,  real_roots[0], real_roots[1], real_roots[2], real_roots[3]);

    if (n == 0)
        return 0;

    int nb_solutions = 0;

    // For each solution of x cal y,and then d1,d2,d3
    for(int i = 0; i < n; i++)
    {
        const double x = real_roots[i];

        // Check reality condition
        if (x <= 0)
            continue;



        //利用公式(14)(15)求解y
        const double H1 = 2*K1*(C13-C23*x);
        if(H1==0)
            continue;

        const double H0 = x*x - K1 - (K1 - 1)* ((K2 - 1)*x*x - 2*C12*K2*x + K2);
        if(H0==0)
            continue;

        const double y = -1*H0/H1;


        //求解d1--公式(4a)
        const double v = 1 + x*x -2*x*C12;
        if (v <= 0)
            continue;
        const double d1 = d12 / std::sqrt(v);


        //d2 d3
        const double d2 = x*d1;
        const double d3 = y*d1;

        lengths[nb_solutions][0] = d1;
        lengths[nb_solutions][1] = d2;
        lengths[nb_solutions][2] = d3;

        nb_solutions++;
    }

    return nb_solutions;


}

bool p3p::align(double M_end[3][3],
                double X0, double Y0, double Z0,
                double X1, double Y1, double Z1,
                double X2, double Y2, double Z2,
                double R[3][3], double T[3])
{
    // Centroids:
    double C_start[3] = {}, C_end[3] = {};
    for(int i = 0; i < 3; i++) C_end[i] = (M_end[0][i] + M_end[1][i] + M_end[2][i]) / 3;
    C_start[0] = (X0 + X1 + X2) / 3;
    C_start[1] = (Y0 + Y1 + Y2) / 3;
    C_start[2] = (Z0 + Z1 + Z2) / 3;

    // Covariance matrix s:
    double s[3 * 3] = {};
    for(int j = 0; j < 3; j++) {
        s[0 * 3 + j] = (X0 * M_end[0][j] + X1 * M_end[1][j] + X2 * M_end[2][j]) / 3 - C_end[j] * C_start[0];
        s[1 * 3 + j] = (Y0 * M_end[0][j] + Y1 * M_end[1][j] + Y2 * M_end[2][j]) / 3 - C_end[j] * C_start[1];
        s[2 * 3 + j] = (Z0 * M_end[0][j] + Z1 * M_end[1][j] + Z2 * M_end[2][j]) / 3 - C_end[j] * C_start[2];
    }

    double Qs[16] = {}, evs[4] = {}, U[16] = {};

    Qs[0 * 4 + 0] = s[0 * 3 + 0] + s[1 * 3 + 1] + s[2 * 3 + 2];
    Qs[1 * 4 + 1] = s[0 * 3 + 0] - s[1 * 3 + 1] - s[2 * 3 + 2];
    Qs[2 * 4 + 2] = s[1 * 3 + 1] - s[2 * 3 + 2] - s[0 * 3 + 0];
    Qs[3 * 4 + 3] = s[2 * 3 + 2] - s[0 * 3 + 0] - s[1 * 3 + 1];

    Qs[1 * 4 + 0] = Qs[0 * 4 + 1] = s[1 * 3 + 2] - s[2 * 3 + 1];
    Qs[2 * 4 + 0] = Qs[0 * 4 + 2] = s[2 * 3 + 0] - s[0 * 3 + 2];
    Qs[3 * 4 + 0] = Qs[0 * 4 + 3] = s[0 * 3 + 1] - s[1 * 3 + 0];
    Qs[2 * 4 + 1] = Qs[1 * 4 + 2] = s[1 * 3 + 0] + s[0 * 3 + 1];
    Qs[3 * 4 + 1] = Qs[1 * 4 + 3] = s[2 * 3 + 0] + s[0 * 3 + 2];
    Qs[3 * 4 + 2] = Qs[2 * 4 + 3] = s[2 * 3 + 1] + s[1 * 3 + 2];

    jacobi_4x4(Qs, evs, U);

    // Looking for the largest eigen value:
    int i_ev = 0;
    double ev_max = evs[i_ev];
    for(int i = 1; i < 4; i++)
        if (evs[i] > ev_max)
            ev_max = evs[i_ev = i];

    // Quaternion:
    double q[4];
    for(int i = 0; i < 4; i++)
        q[i] = U[i * 4 + i_ev];

    double q02 = q[0] * q[0], q12 = q[1] * q[1], q22 = q[2] * q[2], q32 = q[3] * q[3];
    double q0_1 = q[0] * q[1], q0_2 = q[0] * q[2], q0_3 = q[0] * q[3];
    double q1_2 = q[1] * q[2], q1_3 = q[1] * q[3];
    double q2_3 = q[2] * q[3];

    R[0][0] = q02 + q12 - q22 - q32;
    R[0][1] = 2. * (q1_2 - q0_3);
    R[0][2] = 2. * (q1_3 + q0_2);

    R[1][0] = 2. * (q1_2 + q0_3);
    R[1][1] = q02 + q22 - q12 - q32;
    R[1][2] = 2. * (q2_3 - q0_1);

    R[2][0] = 2. * (q1_3 - q0_2);
    R[2][1] = 2. * (q2_3 + q0_1);
    R[2][2] = q02 + q32 - q12 - q22;

    for(int i = 0; i < 3; i++)
        T[i] = C_end[i] - (R[i][0] * C_start[0] + R[i][1] * C_start[1] + R[i][2] * C_start[2]);

    return true;
}

bool p3p::jacobi_4x4(double * A, double * D, double * U)
{
    double B[4] = {}, Z[4] = {};
    double Id[16] = {1., 0., 0., 0.,
                     0., 1., 0., 0.,
                     0., 0., 1., 0.,
                     0., 0., 0., 1.};

    memcpy(U, Id, 16 * sizeof(double));

    B[0] = A[0]; B[1] = A[5]; B[2] = A[10]; B[3] = A[15];
    memcpy(D, B, 4 * sizeof(double));

    for(int iter = 0; iter < 50; iter++) {
        double sum = fabs(A[1]) + fabs(A[2]) + fabs(A[3]) + fabs(A[6]) + fabs(A[7]) + fabs(A[11]);

        if (sum == 0.0)
            return true;

        double tresh =  (iter < 3) ? 0.2 * sum / 16. : 0.0;
        for(int i = 0; i < 3; i++) {
            double * pAij = A + 5 * i + 1;
            for(int j = i + 1 ; j < 4; j++) {
                double Aij = *pAij;
                double eps_machine = 100.0 * fabs(Aij);

                if ( iter > 3 && fabs(D[i]) + eps_machine == fabs(D[i]) && fabs(D[j]) + eps_machine == fabs(D[j]) )
                    *pAij = 0.0;
                else if (fabs(Aij) > tresh) {
                    double hh = D[j] - D[i], t;
                    if (fabs(hh) + eps_machine == fabs(hh))
                        t = Aij / hh;
                    else {
                        double theta = 0.5 * hh / Aij;
                        t = 1.0 / (fabs(theta) + sqrt(1.0 + theta * theta));
                        if (theta < 0.0) t = -t;
                    }

                    hh = t * Aij;
                    Z[i] -= hh;
                    Z[j] += hh;
                    D[i] -= hh;
                    D[j] += hh;
                    *pAij = 0.0;

                    double c = 1.0 / sqrt(1 + t * t);
                    double s = t * c;
                    double tau = s / (1.0 + c);
                    for(int k = 0; k <= i - 1; k++) {
                        double g = A[k * 4 + i], h = A[k * 4 + j];
                        A[k * 4 + i] = g - s * (h + g * tau);
                        A[k * 4 + j] = h + s * (g - h * tau);
                    }
                    for(int k = i + 1; k <= j - 1; k++) {
                        double g = A[i * 4 + k], h = A[k * 4 + j];
                        A[i * 4 + k] = g - s * (h + g * tau);
                        A[k * 4 + j] = h + s * (g - h * tau);
                    }
                    for(int k = j + 1; k < 4; k++) {
                        double g = A[i * 4 + k], h = A[j * 4 + k];
                        A[i * 4 + k] = g - s * (h + g * tau);
                        A[j * 4 + k] = h + s * (g - h * tau);
                    }
                    for(int k = 0; k < 4; k++) {
                        double g = U[k * 4 + i], h = U[k * 4 + j];
                        U[k * 4 + i] = g - s * (h + g * tau);
                        U[k * 4 + j] = h + s * (g - h * tau);
                    }
                }
                pAij++;
            }
        }

        for(int i = 0; i < 4; i++) B[i] += Z[i];
        memcpy(D, B, 4 * sizeof(double));
        memset(Z, 0, 4 * sizeof(double));
    }

    return false;
}


//==================================================================//
//OpenCV源码路径 opencv/modules/calib3d/src/polynom_solver.cpp
int solve_deg2(double a, double b, double c, double & x1, double & x2)
{
    double delta = b * b - 4 * a * c;

    if (delta < 0) return 0;

    double inv_2a = 0.5 / a;

    if (delta == 0) {
        x1 = -b * inv_2a;
        x2 = x1;
        return 1;
    }

    double sqrt_delta = sqrt(delta);
    x1 = (-b + sqrt_delta) * inv_2a;
    x2 = (-b - sqrt_delta) * inv_2a;
    return 2;
}


/// Reference : Eric W. Weisstein. "Cubic Equation." From MathWorld--A Wolfram Web Resource.
/// http://mathworld.wolfram.com/CubicEquation.html
/// \return Number of real roots found.
int solve_deg3(double a, double b, double c, double d,
               double & x0, double & x1, double & x2)
{
    if (a == 0)
    {
        // Solve second order system
        if (b == 0)
        {
            // Solve first order system
            if (c == 0)
                return 0;

            x0 = -d / c;
            return 1;
        }

        x2 = 0;
        return solve_deg2(b, c, d, x0, x1);
    }

    // Calculate the normalized form x^3 + a2 * x^2 + a1 * x + a0 = 0
    double inv_a = 1. / a;
    double b_a = inv_a * b, b_a2 = b_a * b_a;
    double c_a = inv_a * c;
    double d_a = inv_a * d;

    // Solve the cubic equation
    double Q = (3 * c_a - b_a2) / 9;
    double R = (9 * b_a * c_a - 27 * d_a - 2 * b_a * b_a2) / 54;
    double Q3 = Q * Q * Q;
    double D = Q3 + R * R;
    double b_a_3 = (1. / 3.) * b_a;

    if (Q == 0) {
        if(R == 0) {
            x0 = x1 = x2 = - b_a_3;
            return 3;
        }
        else {
            x0 = pow(2 * R, 1 / 3.0) - b_a_3;
            return 1;
        }
    }

    if (D <= 0) {
        // Three real roots
        double theta = acos(R / sqrt(-Q3));
        double sqrt_Q = sqrt(-Q);
        x0 = 2 * sqrt_Q * cos(theta             / 3.0) - b_a_3;
        x1 = 2 * sqrt_Q * cos((theta + 2 * CV_PI)/ 3.0) - b_a_3;
        x2 = 2 * sqrt_Q * cos((theta + 4 * CV_PI)/ 3.0) - b_a_3;

        return 3;
    }

    // D > 0, only one real root
    double AD = pow(fabs(R) + sqrt(D), 1.0 / 3.0) * (R > 0 ? 1 : (R < 0 ? -1 : 0));
    double BD = (AD == 0) ? 0 : -Q / AD;

    // Calculate the only real root
    x0 = AD + BD - b_a_3;

    return 1;
}

/// Reference : Eric W. Weisstein. "Quartic Equation." From MathWorld--A Wolfram Web Resource.
/// http://mathworld.wolfram.com/QuarticEquation.html
/// \return Number of real roots found.
int solve_deg4(double a, double b, double c, double d, double e,
               double & x0, double & x1, double & x2, double & x3)
{
    if (a == 0) {
        x3 = 0;
        return solve_deg3(b, c, d, e, x0, x1, x2);
    }

    // Normalize coefficients
    double inv_a = 1. / a;
    b *= inv_a; c *= inv_a; d *= inv_a; e *= inv_a;
    double b2 = b * b, bc = b * c, b3 = b2 * b;

    // Solve resultant cubic
    double r0, r1, r2;
    int n = solve_deg3(1, -c, d * b - 4 * e, 4 * c * e - d * d - b2 * e, r0, r1, r2);
    if (n == 0) return 0;

    // Calculate R^2
    double R2 = 0.25 * b2 - c + r0, R;
    if (R2 < 0)
        return 0;

    R = sqrt(R2);
    double inv_R = 1. / R;

    int nb_real_roots = 0;

    // Calculate D^2 and E^2
    double D2, E2;
    if (R < 10E-12) {
        double temp = r0 * r0 - 4 * e;
        if (temp < 0)
            D2 = E2 = -1;
        else {
            double sqrt_temp = sqrt(temp);
            D2 = 0.75 * b2 - 2 * c + 2 * sqrt_temp;
            E2 = D2 - 4 * sqrt_temp;
        }
    }
    else {
        double u = 0.75 * b2 - 2 * c - R2,
                v = 0.25 * inv_R * (4 * bc - 8 * d - b3);
        D2 = u + v;
        E2 = u - v;
    }

    double b_4 = 0.25 * b, R_2 = 0.5 * R;
    if (D2 >= 0) {
        double D = sqrt(D2);
        nb_real_roots = 2;
        double D_2 = 0.5 * D;
        x0 = R_2 + D_2 - b_4;
        x1 = x0 - D;
    }

    // Calculate E^2
    if (E2 >= 0) {
        double E = sqrt(E2);
        double E_2 = 0.5 * E;
        if (nb_real_roots == 0) {
            x0 = - R_2 + E_2 - b_4;
            x1 = x0 - E;
            nb_real_roots = 2;
        }
        else {
            x2 = - R_2 + E_2 - b_4;
            x3 = x2 - E;
            nb_real_roots = 4;
        }
    }

    return nb_real_roots;
}



int SolveP3P( cv::InputArray _opoints, cv::InputArray _ipoints,
              cv::InputArray _cameraMatrix, cv::InputArray _distCoeffs,
              cv::OutputArrayOfArrays _rvecs, cv::OutputArrayOfArrays _tvecs, int flags)
{
    cv::Mat opoints = _opoints.getMat(), ipoints = _ipoints.getMat();
    int npoints = std::max(opoints.checkVector(3, CV_32F), opoints.checkVector(3, CV_64F));
    CV_Assert( npoints == std::max(ipoints.checkVector(2, CV_32F), ipoints.checkVector(2, CV_64F)) );
    CV_Assert( npoints == 3 || npoints == 4 );
    CV_Assert( flags == cv::SOLVEPNP_P3P );//仅扩展P3P 未扩展AP3P!!!!!

    if (opoints.cols == 3)
        opoints = opoints.reshape(3);
    if (ipoints.cols == 2)
        ipoints = ipoints.reshape(2);

    cv::Mat cameraMatrix0 = _cameraMatrix.getMat();
    cv::Mat distCoeffs0 = _distCoeffs.getMat();
    cv::Mat cameraMatrix = cv::Mat_<double>(cameraMatrix0);
    cv::Mat distCoeffs = cv::Mat_<double>(distCoeffs0);

    //畸变校正.求无畸变时点的位置
    //针对鱼眼镜头,应采用的函数为 cv::fisheye::undistortPoints()
    //或者,在调用该函数之前进行畸变校正,传参时将畸变设为0;
    //此处调用时已将cameraMatrix传参传入!!!
    cv::Mat undistortedPoints;
    cv::undistortPoints(ipoints, undistortedPoints, cameraMatrix, distCoeffs,cv::Mat(),cameraMatrix);



    std::vector<cv::Mat> Rs, ts, rvecs;

    int solutions = 0;
    if (flags == cv::SOLVEPNP_P3P)
    {
        p3p P3Psolver(cameraMatrix);
        solutions = P3Psolver.solve(Rs, ts, opoints, undistortedPoints);
    }
    else//未扩展
    {

    }

    if (solutions == 0) {
        return 0;
    }

    cv::Mat objPts, imgPts;
    opoints.convertTo(objPts, CV_64F);
    ipoints.convertTo(imgPts, CV_64F);
    if (imgPts.cols > 1)
    {
        imgPts = imgPts.reshape(1);
        imgPts = imgPts.t();
    }
    else
        imgPts = imgPts.reshape(1, 2*imgPts.rows);

    std::vector<double> reproj_errors(solutions);
    for (size_t i = 0; i < reproj_errors.size(); i++)
    {
        cv::Mat rvec;
        cv::Rodrigues(Rs[i], rvec);
        rvecs.push_back(rvec);

        cv::Mat projPts;
        cv::projectPoints(objPts, rvec, ts[i], _cameraMatrix, _distCoeffs, projPts);//将空间点利用外参矩阵投影到图像上

        projPts = projPts.reshape(1, 2*projPts.rows);
        cv::Mat err = imgPts - projPts;//计算重投影点和输入点之间的误差:重投影误差

        err = err.t() * err;
        reproj_errors[i] = err.at<double>(0,0);
    }

    //sort the solutions
    for (int i = 1; i < solutions; i++)
    {
        for (int j = i; j > 0 && reproj_errors[j-1] > reproj_errors[j]; j--)
        {
            std::swap(reproj_errors[j], reproj_errors[j-1]);
            std::swap(rvecs[j], rvecs[j-1]);
            std::swap(ts[j], ts[j-1]);
        }
    }

    int depthRot = _rvecs.fixedType() ? _rvecs.depth() : CV_64F;
    int depthTrans = _tvecs.fixedType() ? _tvecs.depth() : CV_64F;
    _rvecs.create(solutions, 1, CV_MAKETYPE(depthRot, _rvecs.fixedType() && _rvecs.kind() == cv::_InputArray::STD_VECTOR ? 3 : 1));
    _tvecs.create(solutions, 1, CV_MAKETYPE(depthTrans, _tvecs.fixedType() && _tvecs.kind() == cv::_InputArray::STD_VECTOR ? 3 : 1));

    for (int i = 0; i < solutions; i++)
    {
        cv::Mat rvec0, tvec0;
        if (depthRot == CV_64F)
            rvec0 = rvecs[i];
        else
            rvecs[i].convertTo(rvec0, depthRot);

        if (depthTrans == CV_64F)
            tvec0 = ts[i];
        else
            ts[i].convertTo(tvec0, depthTrans);

        if (_rvecs.fixedType() && _rvecs.kind() == cv::_InputArray::STD_VECTOR)
        {
            cv::Mat rref = _rvecs.getMat_();

            if (_rvecs.depth() == CV_32F)
                rref.at<cv::Vec3f>(0,i) = cv::Vec3f(rvec0.at<float>(0,0), rvec0.at<float>(1,0), rvec0.at<float>(2,0));
            else
                rref.at<cv::Vec3d>(0,i) = cv::Vec3d(rvec0.at<double>(0,0), rvec0.at<double>(1,0), rvec0.at<double>(2,0));
        }
        else
        {
            _rvecs.getMatRef(i) = rvec0;
        }

        if (_tvecs.fixedType() && _tvecs.kind() == cv::_InputArray::STD_VECTOR)
        {

            cv::Mat tref = _tvecs.getMat_();

            if (_tvecs.depth() == CV_32F)
                tref.at<cv::Vec3f>(0,i) = cv::Vec3f(tvec0.at<float>(0,0), tvec0.at<float>(1,0), tvec0.at<float>(2,0));
            else
                tref.at<cv::Vec3d>(0,i) = cv::Vec3d(tvec0.at<double>(0,0), tvec0.at<double>(1,0), tvec0.at<double>(2,0));
        }
        else
        {
            _tvecs.getMatRef(i) = tvec0;
        }
    }

    return solutions;
}

调用示例:P3PDemo.cpp:

//
// Created by liheng on 10/2/21.
//

#include <iostream>
#include "p3p.h"


int main()
{
    //1920*1080

    cv::Mat cameraMatrix = (cv::Mat_<double>(3,3) << 983.349f,0,959.5f,
            0,984.953f,539.5f,
            0,0,1);
    cv::Mat distCoeffs = (cv::Mat_<double >(5,1) << -0.0069f,-0.0174f,0.0045f,0,0);
//    cv::Mat distCoeffs = (cv::Mat_<double >(5,1) << 0,0,0,0,0);

    std::vector<cv::Point3d> objectPoints(3);
    objectPoints[0] = cv::Point3f(-1405,260,0);
    objectPoints[1] = cv::Point3f(-415,354,0);
    objectPoints[2] = cv::Point3f(-1405,448,0);

    std::vector<cv::Point2d> imagePoints(3);
    imagePoints[0] = cv::Point2f(506.95f,609.08f);
    imagePoints[1] = cv::Point2f(763.5f,623.3f);
    imagePoints[2] = cv::Point2f(511.12f,659.56f);



    int nSolver = 0;
    std::vector<cv::Mat> rvecs, tvecs;


    std::cout<<"OpenCV's result:"<<std::endl;

    //第4个点
    //objectPoints.emplace_back(-910,542,0);
    //imagePoints.emplace_back(634.82,681.63);

    std::vector<cv::Mat>().swap(rvecs);
    std::vector<cv::Mat>().swap(tvecs);
    nSolver = cv::solveP3P(objectPoints,imagePoints,cameraMatrix,distCoeffs,rvecs,tvecs,cv::SOLVEPNP_P3P);
    for(int i=0;i<nSolver;++i)
    {
        printf("rvecs[%d]=\n",i);
        std::cout<<rvecs[i]<<std::endl;
    }
    for(int i=0;i<nSolver;++i)
    {
        printf("tvecs[%d]=\n",i);
        std::cout<<tvecs[i]<<std::endl;
    }


    std::cout<<"our's result:"<<std::endl;
    std::vector<cv::Mat>().swap(rvecs);
    std::vector<cv::Mat>().swap(tvecs);
    nSolver = SolveP3P(objectPoints,imagePoints,cameraMatrix,distCoeffs,rvecs,tvecs,cv::SOLVEPNP_P3P);
    for(int i=0;i<nSolver;++i)
    {
        printf("rvecs[%d]=\n",i);
        std::cout<<rvecs[i]<<std::endl;
    }
    for(int i=0;i<nSolver;++i)
    {
        printf("tvecs[%d]=\n",i);
        std::cout<<tvecs[i]<<std::endl;
    }
    
    return 0;

}

输出结果如下:

OpenCV's result:
rvecs[0]=[0.05676787660837283;0.1631721865873765;-0.05778765083348027]
rvecs[1]=[-0.3937505222499451;-0.6477959703616123;-0.117545077776493]
tvecs[0]=[-304.7121609195453;-80.32676058043548;3384.398394405537]
tvecs[1]=[-566.274480020068;27.74162315730419;4456.689696059896]

our's result:
rvecs[0]=[0.0567738955468949;0.1601666818930251;-0.05749419176225528]
rvecs[1]=[-0.3937151536817268;-0.6507996780649196;-0.1178830118699575]
tvecs[0]=[-305.7338537790108;-79.66744705042606;3392.541250320854]
tvecs[1]=[-566.8659543357006;27.66665289173454;4455.029987474105]

总结

整理P3P求解过程,其步骤如下:

通过余弦定理构建相机光心与三个空间点以及相对应的夹角的等式关系;
将上述等式关系转换为二元二次方程,通过消元法求解，获得立体几何之间的比值关系,进而获得3个匹配的空间点在相机坐标系下的坐标信息;
通过上述求解的在相机坐标系下的空间坐标和已知的在世界坐标系下的坐标信息，通过ICP的方法获得相机外参;
如果存在第4个点,则利用该点选择误差最小的点.

存在的问题：

P3P只利用3个点的信息.当给定的配对点多于3组时，难以利用更多的信息.
如果3D点或2D点受噪声影响,或者存在误匹配，则算法失效.

代码实现时,数据精度对计算结果的影响,不展开.

参考资料

1.相机位姿求解——P3P问题
2.视觉SLAM位姿求解方法-P3P：基本原理与代码讲解（待更新）
3.三维重建笔记_相机标定(相机矩阵求解)基本概念汇总
4.一元四次方程的求解
5.论文:判定P3P问题正解数目充要条件 --关于四点共面结论的推导

附录

1.求解公式多项式系数matlab代码:

%
%Program:求解多项式f(x)系数
%Author:liheng
%Version:

clear;

syms x;
syms K1 K2;
syms C13 C23 C12;

m=1-K1;
p=2*(K1*C13-x*C23);
q=x^2-K1;

m1=1;
p1=-2*x*C23;
q1=x^2*(1-K2)+2*x*K2*C12-K2;

%求G0~4系数
y=(m1*q-m*q1)^2-(p*m1-p1*m)*(p1*q-p*q1);
G=coeffs(y,x,'All');

%求解H0,H1并化简
%根据(10a)
H1=p*m1-p1*m;
H0=m1*q-m*q1;
%根据(10b)
%H1=m1*q-m*q1;
%H0=p1*q-p*q1;

%simplify(H1)
%simplify(H0)

下面的是我的公众号二维码图片，按需关注。
图注:幼儿园的学霸