目前遇到的loss大致可以分为四大类:基于分布的损失函数(Distribution-based),基于区域的损失函数(Region-based,),基于边界的损失函数(Boundary-based)和基于复合的损失函数(Compounded)。
参考文章:
- 语义分割中的 loss function 最全面汇总
- 一文看尽15种语义分割损失函数(含代码解析)
- 【损失函数合集】超详细的语义分割中的Loss大盘点
- 医学影像分割—Dice Loss
- Pytorch tversky损失函数
- 回归损失函数:Log-Cosh Loss
- MIDL 2019——Boundary loss代码
- 一票难求的MIDL 2019 Day 1-Boundary loss
- 【深度学习】医学图像分割损失函数简介
- JunMa11/SegLoss(推荐仓库)
一、基于分布的损失函数
1.1 cross entropy loss
像素级别的交叉熵损失函数可以说是图像语义分割任务的最常用损失函数,这种损失会逐个检查每个像素,将对每个像素类别的预测结果(概率分布向量,因此在多分类任务中,经常采用 softmax 激活函数将网络输出值进行“归一化”成概率分布)与我们的独热编码标签向量进行比较。
对于每个像素的损失为:
P
i
x
e
r
L
o
s
s
=
?
∑
c
l
a
s
s
e
s
y
t
r
u
e
l
o
g
(
y
p
r
e
d
)
PixerLoss = -\sum_{classes} {y_{true} log \left( y_{pred} \right)}
PixerLoss=?classes∑?ytrue?log(ypred?)
整个图像的损失就是对每个像素的损失求平均值。
特别注意的是,binary entropy loss 是针对类别只有两个的情况,简称 bce loss,损失函数公式为:
B
C
E
L
o
s
s
=
?
y
t
r
u
e
l
o
g
(
y
p
r
e
d
)
?
(
1
?
y
t
r
u
e
)
l
o
g
(
1
?
y
p
r
e
d
)
BCELoss = -y_{true} log \left( y_{pred} \right) - \left(1- y_{true} \right) log \left(1- y_{pred} \right)
BCELoss=?ytrue?log(ypred?)?(1?ytrue?)log(1?ypred?)
代码实现:
#二值交叉熵,这里输入要经过sigmoid处理
import torch
import torch.nn as nn
import torch.nn.functional as F
nn.BCELoss(F.sigmoid(input), target)
#多分类交叉熵, 用这个 loss 前面不需要加 Softmax 层
nn.CrossEntropyLoss(input, target)
1.2 weighted cross entropy loss
由于交叉熵损失会分别评估每个像素的类别预测,然后对所有像素的损失进行平均,因此我们实质上是在对图像中的每个像素进行平等地学习。如果多个类在图像中的分布不均衡,那么这可能导致训练过程由像素数量多的类所主导,即模型会主要学习数量多的类别样本的特征,并且学习出来的模型会更偏向将像素预测为该类别。
FCN论文和U-Net论文中针对这个问题,对输出概率分布向量中的每个值进行加权,即希望模型更加关注数量较少的样本,以缓解图像中存在的类别不均衡问题。比如对于二分类,正负样本比例为1: 99,此时模型将所有样本都预测为负样本,那么准确率仍有99%这么高,但其实该模型没有任何使用价值。
为了平衡这个差距,就对正样本和负样本的损失赋予不同的权重,带权重的二分类损失函数公式如下:
B
C
E
L
o
s
s
=
?
p
o
s
_
w
e
i
g
h
t
×
y
t
r
u
e
l
o
g
(
y
p
r
e
d
)
?
(
1
?
y
t
r
u
e
)
l
o
g
(
1
?
y
p
r
e
d
)
BCELoss = -{pos\_weight} \times y_{true} log \left( y_{pred} \right) - \left(1- y_{true} \right) log \left(1- y_{pred} \right)
BCELoss=?pos_weight×ytrue?log(ypred?)?(1?ytrue?)log(1?ypred?)
p
o
s
_
w
e
i
g
h
t
=
n
u
m
_
n
e
g
n
u
m
_
p
o
s
{pos\_weight} = \frac{num\_neg}{num\_pos}
pos_weight=num_posnum_neg?
要减少假阴性样本的数量,可以增大 pos_weight;要减少假阳性样本的数量,可以减小 pos_weight。
1.3 focal loss
Focal loss是在目标检测领域提出来的。其目的是关注难例(也就是给难分类的样本较大的权重)。对于正样本,使预测概率大的样本(简单样本)得到的loss变小,而预测概率小的样本(难例)loss变得大,从而加强对难例的关注度。
对于较难学习的样本,将 bce loss 修改为:
?
(
1
?
y
p
r
e
d
)
γ
×
y
t
r
u
e
l
o
g
(
y
p
r
e
d
)
?
y
p
r
e
d
γ
(
1
?
y
t
r
u
e
)
l
o
g
(
1
?
y
p
r
e
d
)
-\left(1- y_{pred} \right)^\gamma \times y_{true} log \left( y_{pred} \right) - y_{pred}^\gamma \left(1- y_{true} \right) log \left(1- y_{pred} \right)
?(1?ypred?)γ×ytrue?log(ypred?)?ypredγ?(1?ytrue?)log(1?ypred?)
其中的
γ
\gamma
γ通常设置为2。
举个例子,预测一个正样本,如果预测结果为0.95,这是一个容易学习的样本,有
(
1
?
0.95
)
2
=
0.0025
\left(1- 0.95 \right)^2=0.0025
(1?0.95)2=0.0025 ,损失直接减少为原来的1/400。而如果预测结果为0.5,这是一个难学习的样本,有
(
1
?
0.5
)
2
=
0.25
\left(1- 0.5 \right)^2=0.25
(1?0.5)2=0.25 ,损失减小为原来的1/4,虽然也在减小,但是相对来说,减小的程度小得多。所以通过这种修改,就可以使模型更加专注于学习难学习的样本。
而将这个修改和对正负样本不均衡的修改(即加权系数)合并在一起,就是focal loss:
?
α
(
1
?
y
p
r
e
d
)
γ
×
y
t
r
u
e
l
o
g
(
y
p
r
e
d
)
?
(
1
?
α
)
y
p
r
e
d
γ
(
1
?
y
t
r
u
e
)
l
o
g
(
1
?
y
p
r
e
d
)
-\alpha \left(1- y_{pred} \right)^\gamma \times y_{true} log \left( y_{pred} \right) -\left(1- \alpha \right) y_{pred}^\gamma \left(1- y_{true} \right) log \left(1- y_{pred} \right)
?α(1?ypred?)γ×ytrue?log(ypred?)?(1?α)ypredγ?(1?ytrue?)log(1?ypred?)
下面是多分类的focla loss的代码实现:
class FocalLoss(nn.Module):
"""
copy from: https://github.com/Hsuxu/Loss_ToolBox-PyTorch/blob/master/FocalLoss/FocalLoss.py
This is a implementation of Focal Loss with smooth label cross entropy supported which is proposed in
'Focal Loss for Dense Object Detection. (https://arxiv.org/abs/1708.02002)'
Focal_Loss= -1*alpha*(1-pt)*log(pt)
:param num_class:
:param alpha: (tensor) 3D or 4D the scalar factor for this criterion
:param gamma: (float,double) gamma > 0 reduces the relative loss for well-classified examples (p>0.5) putting more
focus on hard misclassified example
:param smooth: (float,double) smooth value when cross entropy
:param balance_index: (int) balance class index, should be specific when alpha is float
:param size_average: (bool, optional) By default, the losses are averaged over each loss element in the batch.
"""
def __init__(self, apply_nonlin=None, alpha=None, gamma=2, balance_index=0, smooth=1e-5, size_average=True):
super(FocalLoss, self).__init__()
self.apply_nonlin = apply_nonlin
self.alpha = alpha
self.gamma = gamma
self.balance_index = balance_index
self.smooth = smooth
self.size_average = size_average
if self.smooth is not None:
if self.smooth < 0 or self.smooth > 1.0:
raise ValueError('smooth value should be in [0,1]')
def forward(self, logit, target):
if self.apply_nonlin is not None:
logit = self.apply_nonlin(logit)
num_class = logit.shape[1]
if logit.dim() > 2:
# N,C,d1,d2 -> N,C,m (m=d1*d2*...)
logit = logit.view(logit.size(0), logit.size(1), -1)
logit = logit.permute(0, 2, 1).contiguous()
logit = logit.view(-1, logit.size(-1))
target = torch.squeeze(target, 1)
target = target.view(-1, 1)
# print(logit.shape, target.shape)
#
alpha = self.alpha
if alpha is None:
alpha = torch.ones(num_class, 1)
elif isinstance(alpha, (list, np.ndarray)):
assert len(alpha) == num_class
alpha = torch.FloatTensor(alpha).view(num_class, 1)
alpha = alpha / alpha.sum()
elif isinstance(alpha, float):
alpha = torch.ones(num_class, 1)
alpha = alpha * (1 - self.alpha)
alpha[self.balance_index] = self.alpha
else:
raise TypeError('Not support alpha type')
if alpha.device != logit.device:
alpha = alpha.to(logit.device)
idx = target.cpu().long()
one_hot_key = torch.FloatTensor(target.size(0), num_class).zero_()
one_hot_key = one_hot_key.scatter_(1, idx, 1)
if one_hot_key.device != logit.device:
one_hot_key = one_hot_key.to(logit.device)
if self.smooth:
one_hot_key = torch.clamp(
one_hot_key, self.smooth/(num_class-1), 1.0 - self.smooth)
pt = (one_hot_key * logit).sum(1) + self.smooth
logpt = pt.log()
gamma = self.gamma
alpha = alpha[idx]
alpha = torch.squeeze(alpha)
loss = -1 * alpha * torch.pow((1 - pt), gamma) * logpt
if self.size_average:
loss = loss.mean()
else:
loss = loss.sum()
return loss
二、基于区域的损失函数
在讲之前,补充一点前提知识,方便理解下面的公式理解:
TP、TN、FP、FN
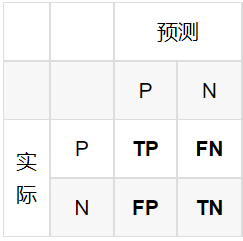
- FN:False Negative,被判定为负样本,但事实上是正样本。
- FP:False Positive,被判定为正样本,但事实上是负样本。
- TN:True Negative,被判定为负样本,事实上也是负样本。
- TP:True Positive,被判定为正样本,事实上也是正样本。
一点记忆小诀窍:第二个字母是预测结果,第一个字母是判断预测结果对不对。
与集合的关系:
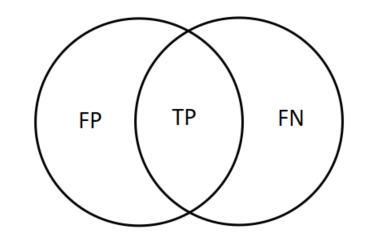
2.1 dice loss
Dice系数:是用来度量集合相似度的度量函数,通常用于计算两个样本之间的像素之间的相似度,度量范围为 0~1,其中 Dice 系数为1表示完全重叠。Dice 系数最初是用于二进制数据的,可以计算为:
D
i
c
e
=
2
∣
X
∩
Y
∣
∣
X
∣
+
∣
Y
∣
=
2
T
P
2
T
P
+
F
N
+
F
P
Dice = \frac{2|X\cap Y|}{|X| + |Y| } = \frac{2TP}{2TP+FN+FP}
Dice=∣X∣+∣Y∣2∣X∩Y∣?=2TP+FN+FP2TP?
∣
X
∩
Y
∣
|X\cap Y|
∣X∩Y∣代表集合X和Y之间的公共元素,并且
∣
X
∣
|X|
∣X∣代表集合A中的元素数量(对于集合Y同理)。分子中之所以有一个系数2是因为分母中有重复计算
∣
X
∩
Y
∣
|X\cap Y|
∣X∩Y∣的原因。其TP 为真阳性样本,FP 为假阳性样本,FN 为假阴性样本
针对分割任务来说,
∣
X
∣
|X|
∣X∣代表的就是预测的分割图像,而
∣
Y
∣
|Y|
∣Y∣表示的就是Ground Truth分割图像。
但是为了设计一个可以最小化的损失,可以简单地使用1-dice作为loss表现形式,但这是不可导的,原因在于dice计算过程中对于网络输出的预测图像的概率值使用了阈值转换为二进制掩码。因此为了可导,我们直接使用网络输出的预测概率,那么
∣
A
∩
B
∣
|A\cap B|
∣A∩B∣就可以近似为(图片来源:医学影像分割—Dice Loss):
(1)预测的概率掩码和标签掩码之间的逐元素乘法
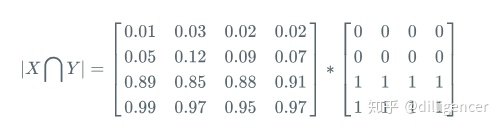
(2)然后对结果矩阵求和

同意对于|X|和|Y|,这里可以采用直接元素相加,也可以采用元素平方求和的方法:
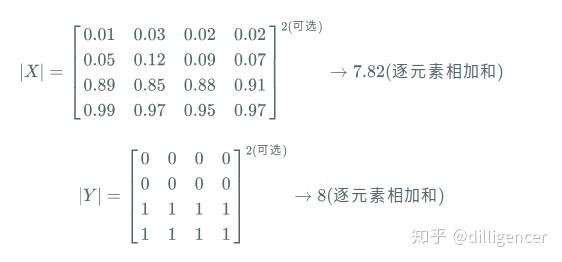
所以dice loss又被称为soft dice loss,这是因为我们直接使用预测出的概率,而不是使用阈值将其转换成一个二进制掩码。
故对于每个类别的mask,都计算一个 Dice 损失(是否采用平方是可选的):
D
i
c
e
=
1
?
2
∑
p
i
x
e
l
s
y
t
r
u
e
y
p
r
e
d
∑
p
i
x
e
l
s
(
y
t
r
u
e
+
y
p
r
e
d
)
Dice = 1- \frac{ 2 \sum_{pixels} y_{true}y_{pred}} { \sum_{pixels} \left( y_{true}{} + y_{pred} \right)}
Dice=1?∑pixels?(ytrue?+ypred?)2∑pixels?ytrue?ypred??
然后将每个类的dice损失求和取平均,得到最后的loss。
下面dice loss的代码实现:
import torch
from typing import List
from torch import Tensor, einsum
class DiceLoss():
def __init__(self, idc: List[int], smooth: float=1e-10):
# Self.idc is used to filter out some classes of the target mask. Use fancy indexing
self.idc: List[int] = idc
self.smooth = smooth
def simplex(self, t: Tensor, axis=1) -> bool:
_sum = t.sum(axis).type(torch.float32)
_ones = torch.ones_like(_sum, dtype=torch.float32)
return torch.allclose(_sum, _ones)
def __call__(self, probs: Tensor, target: Tensor) -> Tensor:
"""
probs: (B, C, H, W)
target: (B, C, H, W)
"""
assert self.simplex(probs) and self.simplex(target)
pc = probs[:, self.idc, ...].type(torch.float32)
tc = target[:, self.idc, ...].type(torch.float32)
intersection: Tensor = einsum("bcwh,bcwh->bc", pc, tc)
union: Tensor = (einsum("bkwh->bk", pc) + einsum("bkwh->bk", tc))
divided: Tensor = torch.ones_like(intersection) - (2 * intersection + self.smooth) / (union + self.smooth)
loss = divided.mean()
return loss
2.2 IOU loss
IoU 的计算公式和dice计算公式很像,区别就是 TP 只计算一次。
I
O
U
=
∣
X
∩
Y
∣
∣
X
∣
+
∣
Y
∣
?
∣
X
∩
Y
∣
=
T
P
T
P
+
F
N
+
F
P
IOU = \frac{|X\cap Y|}{|X| + |Y| - |X\cap Y|} = \frac{TP}{TP+FN+FP}
IOU=∣X∣+∣Y∣?∣X∩Y∣∣X∩Y∣?=TP+FN+FPTP?
IOU Loss和Dice Loss一样属于metric learning的衡量方式,也是使用预测的概率值,公式定义如下:
I
O
U
=
1
?
∣
X
∩
Y
∣
∣
X
∣
+
∣
Y
∣
?
∣
X
∩
Y
∣
IOU = 1- \frac{|X\cap Y|}{|X| + |Y| - |X\cap Y|}
IOU=1?∣X∣+∣Y∣?∣X∩Y∣∣X∩Y∣?
和Dice Loss一样仍然存在训练过程不稳定的问题,IOU Loss在分割任务中应该是不怎么用的,在代码实现非常简单,在上面Dice Loss的基础上改一下即可。
2.3 Generalized Dice loss
论文题目:Generalized Overlap Measures for Evaluation and Validation in Medical Image Analysis
Dice Loss对小目标的预测是十分不利的,因为一旦小目标有部分像素预测错误,就可能会引起Dice系数大幅度波动,导致梯度变化大训练不稳定。另外从上面的代码实现可以发现,Dice Loss针对的是某一个特定类别的分割的损失。当类似于病灶分割有多个场景的时候一般都会使用多个Dice Loss,所以Generalized Dice loss就是将多个类别的Dice Loss进行整合,使用一个指标作为分割结果的量化指标。GDL Loss在类别数为2时公式如下:
I
O
U
=
1
?
2
∑
l
=
1
2
w
l
∑
n
r
l
n
p
l
n
∑
l
=
1
2
w
l
∑
n
(
r
l
n
+
p
l
n
)
IOU = 1-2\frac{\sum_{l=1}^2 w_l \sum_{n}r_{ln}p_{ln}} {\sum_{l=1}^2 w_l \sum_{n}(r_{ln}+p_{ln})}
IOU=1?2∑l=12?wl?∑n?(rln?+pln?)∑l=12?wl?∑n?rln?pln??
其中
r
l
n
r_{ln}
rln?表示类别
l
l
l在第
n
n
n个位置的真实像素类别,而
p
l
n
p_{ln}
pln?表示相应的预测概率值,
w
l
w_l
wl?表示每个类别的权重。
w
l
w_l
wl?的公式为:
w
l
=
1
∑
i
=
1
n
r
l
n
2
w_l = \frac{1} {\sum_{i=1}^n r_{ln}^2 }
wl?=∑i=1n?rln2?1?
代码实现:
import torch
from typing import List
from torch import Tensor, einsum
class GeneralizedDiceLoss():
def __init__(self, idc: List[int], smooth: float=1e-10):
# Self.idc is used to filter out some classes of the target mask. Use fancy indexing
self.idc: List[int] = idc
self.smooth = smooth
def simplex(self, t: Tensor, axis=1) -> bool:
_sum = t.sum(axis).type(torch.float32)
_ones = torch.ones_like(_sum, dtype=torch.float32)
return torch.allclose(_sum, _ones)
def __call__(self, probs: Tensor, target: Tensor) -> Tensor:
"""
probs: (B, C, H, W)
target: (B, C, H, W)
"""
assert self.simplex(probs) and self.simplex(target)
pc = probs[:, self.idc, ...].type(torch.float32)
tc = target[:, self.idc, ...].type(torch.float32)
w: Tensor = 1 / ((einsum("bkwh->bk", tc).type(torch.float32) + self.smooth) ** 2)
intersection: Tensor = w * einsum("bkwh,bkwh->bk", pc, tc)
union: Tensor = w * (einsum("bkwh->bk", pc) + einsum("bkwh->bk", tc))
divided: Tensor = 1 - 2 * (einsum("bk->b", intersection) + self.smooth) / (einsum("bk->b", union) + self.smooth)
loss = divided.mean()
return loss
2.4 Tversky Loss
paper: https://arxiv.org/pdf/1706.05721.pdf
公式为:
T
(
X
,
Y
)
=
∣
X
∩
Y
∣
∣
X
∩
Y
∣
+
α
∣
X
?
Y
∣
+
β
∣
Y
?
X
∣
T(X,Y) = \frac{|X\cap Y|}{|X\cap Y|+\alpha|X-Y|+\beta|Y-X|}
T(X,Y)=∣X∩Y∣+α∣X?Y∣+β∣Y?X∣∣X∩Y∣?
其中
∣
X
∣
|X|
∣X∣表示预测的分割图像,而
∣
Y
∣
|Y|
∣Y∣表示Ground Truth分割图像。
Tversky系数是Dice系数和 Jaccard 系数(就是IOU系数)的广义系数。当设置α=β=0.5,此时Tversky系数就是Dice系数。而当设置α=β=1时,此时Tversky系数就是Jaccard系数。其中
∣
X
?
Y
∣
|X-Y|
∣X?Y∣代表FP(假阳性),
∣
Y
?
X
∣
|Y-X|
∣Y?X∣代表FN(假阴性),通过调整
α
\alpha
α和
β
\beta
β这两个超参数可以控制这两者之间的权衡,进而影响召回率等指标。
一个简单的实现:
def tversky_loss(inputs, targets, beta=0.7, weights=None):
batch_size = targets.size(0)
loss = 0.0
for i in range(batch_size):
prob = inputs[i]
ref = targets[i]
alpha = 1.0-beta
tp = (ref*prob).sum()
fp = ((1-ref)*prob).sum()
fn = (ref*(1-prob)).sum()
tversky = tp/(tp + alpha*fp + beta*fn)
loss = loss + (1-tversky)
return loss/batch_size
2.5 Sensitivity Specificity Loss
首先敏感性就是召回率,检测出确实有病的能力:
S
e
n
s
i
t
i
v
i
t
y
=
T
P
T
P
+
F
N
Sensitivity = \frac{TP}{TP+FN}
Sensitivity=TP+FNTP?
特异性,检测出确实没病的能力:
S
p
e
c
i
f
i
c
i
t
y
=
T
N
T
N
+
F
P
Specificity = \frac{TN}{TN+FP}
Specificity=TN+FPTN?
而Sensitivity Specificity Loss为:
S
S
=
λ
∑
n
=
1
N
(
r
n
?
p
n
)
2
r
n
∑
n
=
1
N
r
n
+
?
+
(
1
?
λ
)
∑
n
=
1
N
(
r
n
?
p
n
)
2
(
1
?
r
n
)
∑
n
=
1
N
(
1
?
r
n
)
+
?
SS = \lambda \frac{\sum_{n=1}^N(r_n-p_n)^2r_n}{\sum_{n=1}^Nr_n+\epsilon} + (1-\lambda) \frac{\sum_{n=1}^N(r_n-p_n)^2(1-r_n)}{\sum_{n=1}^N(1-r_n)+\epsilon}
SS=λ∑n=1N?rn?+?∑n=1N?(rn??pn?)2rn??+(1?λ)∑n=1N?(1?rn?)+?∑n=1N?(rn??pn?)2(1?rn?)?
其中左边为病灶像素的错误率即,1?Sensitivity,而不是正确率,所以设置λ 为0.05。其中
(
r
n
?
p
n
)
2
(r_n-p_n)^2
(rn??pn?)2是为了得到平滑的梯度。
代码:
import torch
from torch import nn
import numpy as np
def sum_tensor(inp, axes, keepdim=False):
# copy from: https://github.com/MIC-DKFZ/nnUNet/blob/master/nnunet/utilities/tensor_utilities.py
axes = np.unique(axes).astype(int)
if keepdim:
for ax in axes:
inp = inp.sum(int(ax), keepdim=True)
else:
for ax in sorted(axes, reverse=True):
inp = inp.sum(int(ax))
return inp
class SSLoss(nn.Module):
def __init__(self, apply_nonlin=None, batch_dice=False, do_bg=True, smooth=1.,
square=False):
"""
Sensitivity-Specifity loss
paper: http://www.rogertam.ca/Brosch_MICCAI_2015.pdf
tf code: https://github.com/NifTK/NiftyNet/blob/df0f86733357fdc92bbc191c8fec0dcf49aa5499/niftynet/layer/loss_segmentation.py#L392
"""
super(SSLoss, self).__init__()
self.square = square
self.do_bg = do_bg
self.batch_dice = batch_dice
self.apply_nonlin = apply_nonlin
self.smooth = smooth
self.r = 0.1 # weight parameter in SS paper
def forward(self, net_output, gt, loss_mask=None):
shp_x = net_output.shape
shp_y = gt.shape
# class_num = shp_x[1]
with torch.no_grad():
if len(shp_x) != len(shp_y):
gt = gt.view((shp_y[0], 1, *shp_y[1:]))
if all([i == j for i, j in zip(net_output.shape, gt.shape)]):
# if this is the case then gt is probably already a one hot encoding
y_onehot = gt
else:
gt = gt.long()
y_onehot = torch.zeros(shp_x)
if net_output.device.type == "cuda":
y_onehot = y_onehot.cuda(net_output.device.index)
y_onehot.scatter_(1, gt, 1)
if self.batch_dice:
axes = [0] + list(range(2, len(shp_x)))
else:
axes = list(range(2, len(shp_x)))
if self.apply_nonlin is not None:
net_output = self.apply_nonlin(net_output)
# no object value
bg_onehot = 1 - y_onehot
squared_error = (y_onehot - net_output) ** 2
specificity_part = sum_tensor(squared_error * y_onehot, axes) / (sum_tensor(y_onehot, axes) + self.smooth)
sensitivity_part = sum_tensor(squared_error * bg_onehot, axes) / (sum_tensor(bg_onehot, axes) + self.smooth)
ss = self.r * specificity_part + (1 - self.r) * sensitivity_part
if not self.do_bg:
if self.batch_dice:
ss = ss[1:]
else:
ss = ss[:, 1:]
ss = ss.mean()
return ss
2.6 Log-Cosh Dice Loss
dice loss由于其非凸性,一般训练起来都不是很稳定,甚至出现训练多次都无法获得最佳结果的情况。跟Lovsz-softmax损失通过添加使用Lovsz扩展的平滑来解决IOU loss的非凸性问题类似,Log-Cosh Dice Loss通过Log-Cosh方法来平滑区域。Log-Cosh是应用于回归任务中的一种损失函数,它比L2损失更平滑。Log-cosh是预测误差的双曲余弦的对数(有兴趣可以去了解一下)。
Log-cosh的函数表达式为:
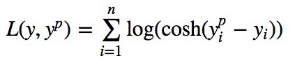
cosh(x)函数图像为:
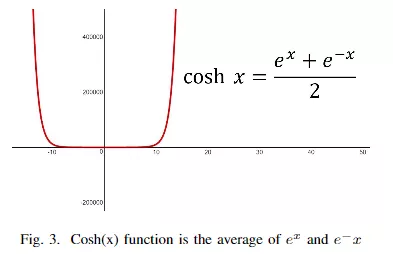
log(x)函数图像为:
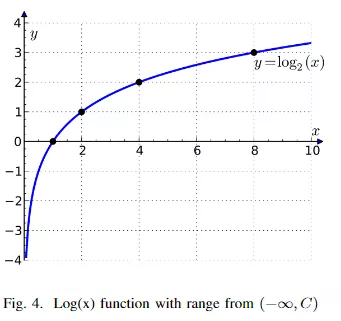
两者合起来就是:
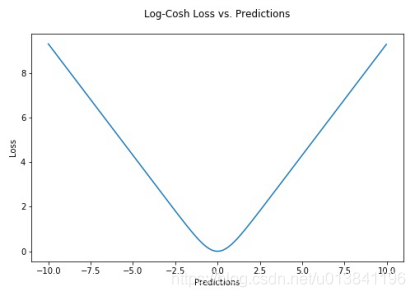
Log-Cosh Dice Loss就是将x值替换成dice loss。全部合起来就是:
L
l
c
?
d
i
c
e
=
l
o
g
(
c
o
s
h
(
D
i
c
e
l
L
o
s
s
)
)
L_{lc-dice} = log(cosh(DicelLoss))
Llc?dice?=log(cosh(DicelLoss))
一个简单伪代码实现:
def log_cosh_dice_loss(y_true, y_pred):
x = dice_loss(y_true, y_pred)
return torch.log((torch.exp(x) + torch.exp(-x)) / 2.0)
三、 基于边界的损失函数
因为几个基于边界的损失函数都出现距离图的这个概念,在这里简要说明一下,距离图可以认为是图像中非零点到最近背景点(像素值为0)的距离(当然还有其他形式的距离图)。举例说明一下:
(1)离最近背景点距离为
2
\sqrt 2
2? ,用绿色标出
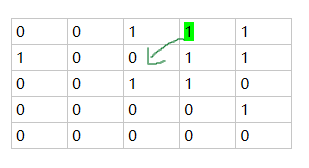
(2)离最近背景点距离为2 ,用橘色标出

(3)以此类推,整个距离图如下所示:

当然,这个距离转换已经有成熟的库封装好了,不需要我们自己写。只需要:
from scipy.ndimage import distance_transform_edt
3.1 Hausdorff Distance Loss
Hausdorff Distance Loss(HD)是分割方法用来跟踪模型性能的度量。它定义为:
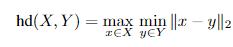
任何分割模型的目的都是为了最大化Hausdorff距离,但是由于其非凸性,因此并未广泛用作损失函数。有研究者提出了基于Hausdorff距离的损失函数的3个变量,它们都结合了度量用例,并确保损失函数易于处理。
具体的原理可以看原paper(公式太多了,让人头秃):https://arxiv.org/pdf/1904.10030v1.pdf
从相关代码的实现上可以看出,该loss可以近似认为是L2 loss的加权。问题的关键在于如何结合距离图(或者对距离图作一定的变换)计算对应的权重系数。
具体距离图变换原理就不讲(暂时还不理解),来看代码:
def distance_field(self, img: np.ndarray) -> np.ndarray:
field = np.zeros_like(img)
for batch in range(len(img)):
fg_mask = img[batch] > 0.5
if fg_mask.any():
bg_mask = ~fg_mask
fg_dist = distance_transform_edt(fg_mask)
bg_dist = distance_transform_edt(bg_mask)
field[batch] = fg_dist + bg_dist
return field
整个距离图转换计算都不难,,对于某一类的mask计算其前景和背景的距离图,然后再把两者加起来。比如说,某一类的mask如下:

0为背景,1为前景,那么其前景的距离图fg_dist为:

其背景的距离图为:

两者距离图加起来就为:

接下来很简单,分别计算pred和target的距离图变换,然后乘于一个
α
\alpha
α系数并相加,最后得到的结果作为L2范式的权重系数。
pred_dt = torch.from_numpy(self.distance_field(pred.cpu().numpy())).float()
target_dt = torch.from_numpy(self.distance_field(target.cpu().numpy())).float()
distance = pred_dt ** self.alpha + target_dt ** self.alpha
pred_error = (pred - target) ** 2
dt_field = pred_error * distance
loss = dt_field.mean()
下面是两分类情况下且网络输出为单通道的 Hausdorff Distance Loss实现,当然多分类情况也不复杂,稍加修改代码就行了。
import numpy as np
import torch
from torch import nn
from scipy.ndimage.morphology import distance_transform_edt
"""
Hausdorff loss implementation based on paper:
https://arxiv.org/pdf/1904.10030.pdf
copy pasted from - all credit goes to original authors:
https://github.com/SilmarilBearer/HausdorffLoss
"""
class HausdorffDTLoss(nn.Module):
"""Binary Hausdorff loss based on distance transform"""
def __init__(self, alpha=2.0, **kwargs):
super(HausdorffDTLoss, self).__init__()
self.alpha = alpha
@torch.no_grad()
def distance_field(self, img: np.ndarray) -> np.ndarray:
field = np.zeros_like(img)
for batch in range(len(img)):
fg_mask = img[batch] > 0.5
if fg_mask.any():
bg_mask = ~fg_mask
fg_dist = distance_transform_edt(fg_mask)
bg_dist = distance_transform_edt(bg_mask)
field[batch] = fg_dist + bg_dist
return field
def forward(
self, pred: torch.Tensor, target: torch.Tensor, debug=False
) -> torch.Tensor:
"""
Uses one binary channel: 1 - fg, 0 - bg
pred: (b, 1, x, y, z) or (b, 1, x, y)
target: (b, 1, x, y, z) or (b, 1, x, y)
"""
assert pred.dim() == 4 or pred.dim() == 5, "Only 2D and 3D supported"
assert (
pred.dim() == target.dim()
), "Prediction and target need to be of same dimension"
# pred = torch.sigmoid(pred)
pred_dt = torch.from_numpy(self.distance_field(pred.cpu().numpy())).float()
target_dt = torch.from_numpy(self.distance_field(target.cpu().numpy())).float()
pred_error = (pred - target) ** 2
distance = pred_dt ** self.alpha + target_dt ** self.alpha
dt_field = pred_error * distance
loss = dt_field.mean()
if debug:
return (
loss.cpu().numpy(),
(
dt_field.cpu().numpy()[0, 0],
pred_error.cpu().numpy()[0, 0],
distance.cpu().numpy()[0, 0],
pred_dt.cpu().numpy()[0, 0],
target_dt.cpu().numpy()[0, 0],
),
)
else:
return loss
3.2 Shape-aware Loss
顾名思义,Shape-aware Loss考虑了形状。通常,所有损失函数都在像素级起作用,Shape-aware Loss会计算平均点到曲线的欧几里得距离,即预测分割到ground truth的曲线周围点之间的欧式距离,并将其用作交叉熵损失函数的系数,具体定义如下:(CE指交叉熵损失函数)
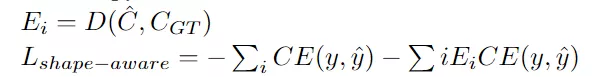
D就是距离转换函数,得到的值就作为权重系数。
当然上面的描述会让人感觉很懵,具体可以去看paper:Distance Map Loss Penalty Term for Semantic Segmentation
没有找到对应的复现,只找到了dice loss的形式,但是思想是一致的,就是对距离图作变换,然后作为某个loss的加权形式。
先看看距离图变换函数是怎么实现的:
def compute_edts_forPenalizedLoss(GT):
"""
GT.shape = (batch_size, x,y,z)
only for binary segmentation
"""
res = np.zeros(GT.shape)
for i in range(GT.shape[0]):
posmask = (GT[i]).astype(np.bool)
negmask = ~posmask
pos_edt = distance_transform_edt(posmask)
pos_edt = (np.max(pos_edt)-pos_edt)*posmask
neg_edt = distance_transform_edt(negmask)
neg_edt = (np.max(neg_edt)-neg_edt)*negmask
res[i] = pos_edt/np.max(pos_edt) + neg_edt/np.max(neg_edt)
return res
如果输入的mask如下的话:

那么输出的距离变换为:

至于为什么要这样算,就要看论文了。
整个代码实现为:
import numpy as np
import torch
from torch import nn
from scipy.ndimage.morphology import distance_transform_edt
def softmax_helper(x):
# copy from: https://github.com/MIC-DKFZ/nnUNet/blob/master/nnunet/utilities/nd_softmax.py
rpt = [1 for _ in range(len(x.size()))]
rpt[1] = x.size(1)
x_max = x.max(1, keepdim=True)[0].repeat(*rpt)
e_x = torch.exp(x - x_max)
return e_x / e_x.sum(1, keepdim=True).repeat(*rpt)
def compute_edts_forPenalizedLoss(GT):
"""
GT.shape = (batch_size, x,y,z)
only for binary segmentation
"""
res = np.zeros(GT.shape)
for i in range(GT.shape[0]):
posmask = GT[i]
negmask = ~posmask
pos_edt = distance_transform_edt(posmask)
pos_edt = (np.max(pos_edt) - pos_edt) * posmask
neg_edt = distance_transform_edt(negmask)
neg_edt = (np.max(neg_edt) - neg_edt) * negmask
res[i] = pos_edt / np.max(pos_edt) + neg_edt / np.max(neg_edt)
return res
class DistBinaryDiceLoss(nn.Module):
"""
Distance map penalized Dice loss
Motivated by: https://openreview.net/forum?id=B1eIcvS45V
Distance Map Loss Penalty Term for Semantic Segmentation
"""
def __init__(self, smooth=1e-5):
super(DistBinaryDiceLoss, self).__init__()
self.smooth = smooth
def forward(self, net_output, gt):
"""
net_output: (batch_size, 2, x,y,z)
target: ground truth, shape: (batch_size, 1, x,y,z)
"""
net_output = softmax_helper(net_output)
# one hot code for gt
with torch.no_grad():
if len(net_output.shape) != len(gt.shape):
gt = gt.view((gt.shape[0], 1, *gt.shape[1:]))
if all([i == j for i, j in zip(net_output.shape, gt.shape)]):
# if this is the case then gt is probably already a one hot encoding
y_onehot = gt
else:
gt = gt.long()
y_onehot = torch.zeros(net_output.shape)
if net_output.device.type == "cuda":
y_onehot = y_onehot.cuda(net_output.device.index)
y_onehot.scatter_(1, gt, 1)
gt_temp = gt[:, 0, ...].type(torch.float32)
with torch.no_grad():
dist = compute_edts_forPenalizedLoss(gt_temp.cpu().numpy() > 0.5) + 1.0
# print('dist.shape: ', dist.shape)
dist = torch.from_numpy(dist)
if dist.device != net_output.device:
dist = dist.to(net_output.device).type(torch.float32)
tp = net_output * y_onehot
tp = torch.sum(tp[:, 1, ...] * dist, (1, 2, 3))
dc = (2 * tp + self.smooth) / (torch.sum(net_output[:, 1, ...], (1, 2, 3)) + torch.sum(y_onehot[:, 1, ...],
(1, 2, 3)) + self.smooth)
dc = dc.mean()
return -dc
可以看只对真实标签的背景通道做距离变换,,然后作为dice loss的权重系数。
3.3 Boundary loss
Boundary loss由Boundary loss for highly unbalanced segmentation这篇文章提出,用于图像分割loss,作者的实验结果表明dice loss+Boundary loss效果非常好,一个是利用区域,一个利用边界。作者对这两个loss的用法是给他们一个权重,训练初期dice loss很高,随着训练进行,Boundary loss比例增加,也就是说越到训练后期越关注边界的准确,边界处理得更细一些。
如果详细对比后就会发现,本文上面提到的两种基于边界的loss的思想都是很接近的。都是将distance map当做权重来作为某类loss的权重系数。Boundary loss也不例外,因此关于其distance map背后的数学原理也不会涉及(也看不懂),具体的一些公式解释可以看这一篇博客:一票难求的MIDL 2019 Day 1-Boundary loss
直接上源码,distance map的变换代码如下:
def one_hot2dist(seg: np.ndarray) -> np.ndarray:
C: int = len(seg)
res = np.zeros_like(seg)
for c in range(C):
posmask = seg[c].astype(np.bool)
if posmask.any():
negmask = ~posmask
# print('negmask:', negmask)
# print('distance(negmask):', distance(negmask))
res[c] = distance_transform_edt(negmask) * negmask - (distance_transform_edt(posmask) - 1) * posmask
# print('res[c]', res[c])
return res
假设某一类别的mask如下:

那么得到的distance map就为:

可以看大边界处的权重为0,mask内部为负值,背景区域离边界越远权重值越大。
import numpy as np
import torch
from typing import List, Set, Iterable
from torch import Tensor, einsum
def uniq(a: Tensor) -> Set:
return set(torch.unique(a.cpu()).numpy())
def sset(a: Tensor, sub: Iterable) -> bool:
return uniq(a).issubset(sub)
def simplex(t: Tensor, axis=1) -> bool:
_sum = t.sum(axis).type(torch.float32)
_ones = torch.ones_like(_sum, dtype=torch.float32)
return torch.allclose(_sum, _ones)
def one_hot(t: Tensor, axis=1) -> bool:
return simplex(t, axis) and sset(t, [0, 1])
class SurfaceLoss():
def __init__(self, **kwargs):
# Self.idc is used to filter out some classes of the target mask. Use fancy indexing
self.idc: List[int] = kwargs["idc"]
print(f"Initialized {self.__class__.__name__} with {kwargs}")
def __call__(self, probs: Tensor, dist_maps: Tensor) -> Tensor:
# assert simplex(probs)
assert not one_hot(dist_maps)
pc = probs[:, self.idc, ...].type(torch.float32)
dc = dist_maps[:, self.idc, ...].type(torch.float32)
multipled = einsum("bkwh,bkwh->bkwh", pc, dc)
loss = multipled.mean()
return loss
可以看是将distance map与预测值相乘直接计算loss。
因此,根据上面的distance map的可视化结果看出,如果预测边界小于或者完全符合真实边界并被真实边界包围,这时候loss为负。根据实测,一般训练到最后,Boundary loss会为负值。这也部分解释了论文的实验结果,单独使用不work,与其他loss(如dice loss)联合使用会取得一个不错的结果。
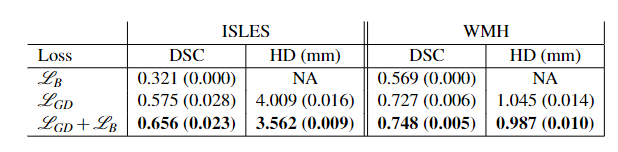
还有论文中联合dice loss(当然也可以是其他loss)使用的公式为:
L
o
s
s
=
α
D
i
c
e
+
(
1
?
α
)
B
o
u
n
d
a
r
y
Loss = αDice+(1-α)Boundary
Loss=αDice+(1?α)Boundary
这里α初始值1,每过一轮减小0.01。但是本人在一些数据集训练后发现这种α递减的方式不一定有效,反而是将其固定为0.01取的不错的效果,至于哪种方式有效,只能各自尝试了。
四、基于复合的损失函数
4.1 combo loss
combo loss 是CE和dice loss 的加权和。试图利用Dice损失解决类不平衡问题的灵活性,同时使用交叉熵进行曲线平滑。
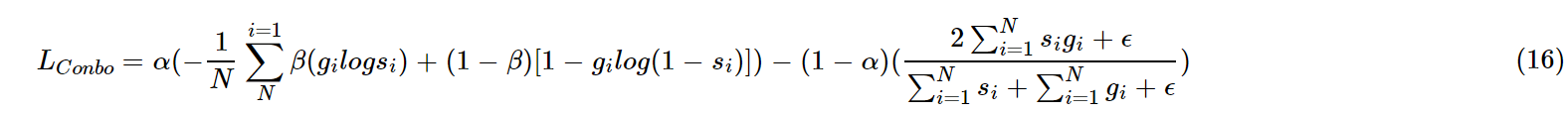
从形式上是加权的BCE和Dice loss的组合。根据查到一些资料可以得到一个认知,在数据较为均衡的情况下有所改善,但是在数据极度不均衡的情况下交叉熵Loss会在迭代几个Epoch之后远远小于Dice Loss,这个组合Loss会退化为Dice Loss。
4.2 Exponential Logarithmic loss
这个Loss是MICCAI 2018的论文3D Segmentation with Exponential LogarithmicLoss for Highly Unbalanced Object Sizes提出来的。公式如下:
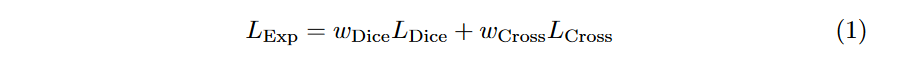
这里增加了两个参数权重分别为
w
D
i
c
e
w_{Dice}
wDice?和
w
C
r
o
s
s
w_{Cross}
wCross?,而
L
D
i
c
e
L_{Dice}
LDice?为指数log Dice损失,
L
C
r
o
s
s
L_{Cross}
LCross?为指数交叉熵损失。公式如下:
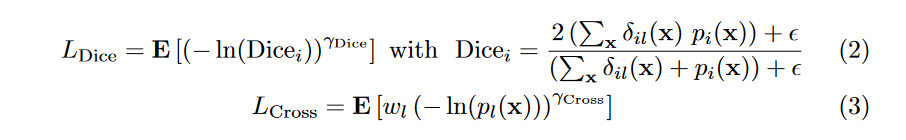
其中,
x
x
x表示像素位置,
i
i
i表示类别标签,
l
l
l表示位置
x
x
x处的ground truth类别,
p
i
(
x
)
p_i(x)
pi?(x)表示经过softmax操作之后的概率值。其中:
W
l
=
(
∑
k
f
k
f
l
)
0
.
5
W_l=( \frac{\sum_k f_k}{f_l} )^0.5
Wl?=(fl?∑k?fk??)0.5其中
f
k
f_k
fk?表示标签
k
k
k出现的频率,这个参数可以减小出现频率较高的类别权重。
γ
D
i
c
e
\gamma_{Dice}
γDice?和
γ
C
r
o
s
s
\gamma_{Cross}
γCross?可以提升函数的非线性。
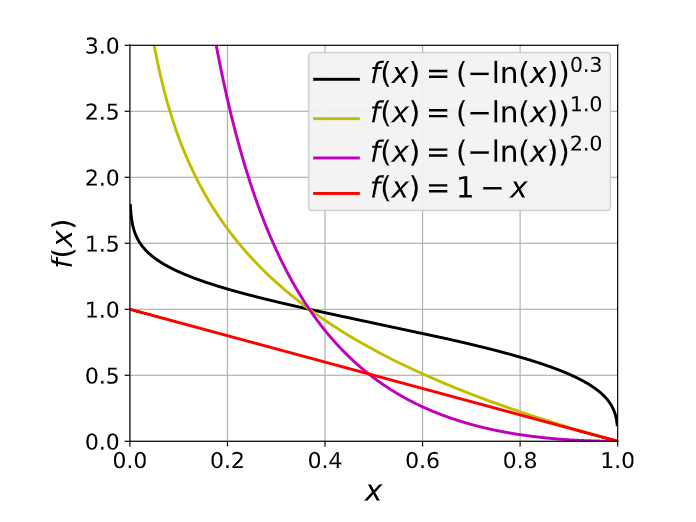
从形式来看,是对CE和dice loss进行指数和对数变换。这样网络就可以被迫的关注预测不准的部分。