目录
RNN
RNN的发展
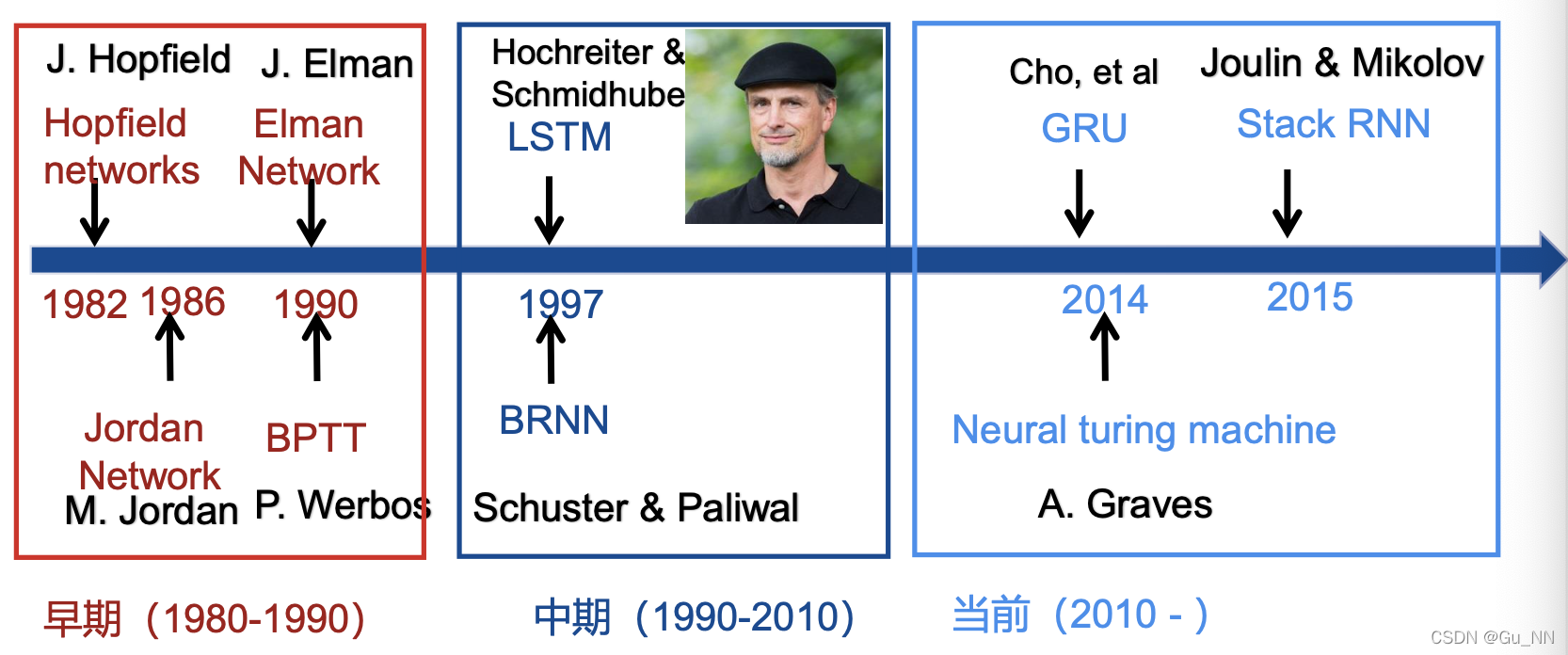
RNN和Markov模型
共同点
描述数据时间上的依存关系
Markov模型的局限性
- 仅对有限离散状态的描述
- 仅描述当前时刻和前一时刻之间关系(无记忆性)
- 隐藏层数的增加不会让模型状态值更复杂
一般结构
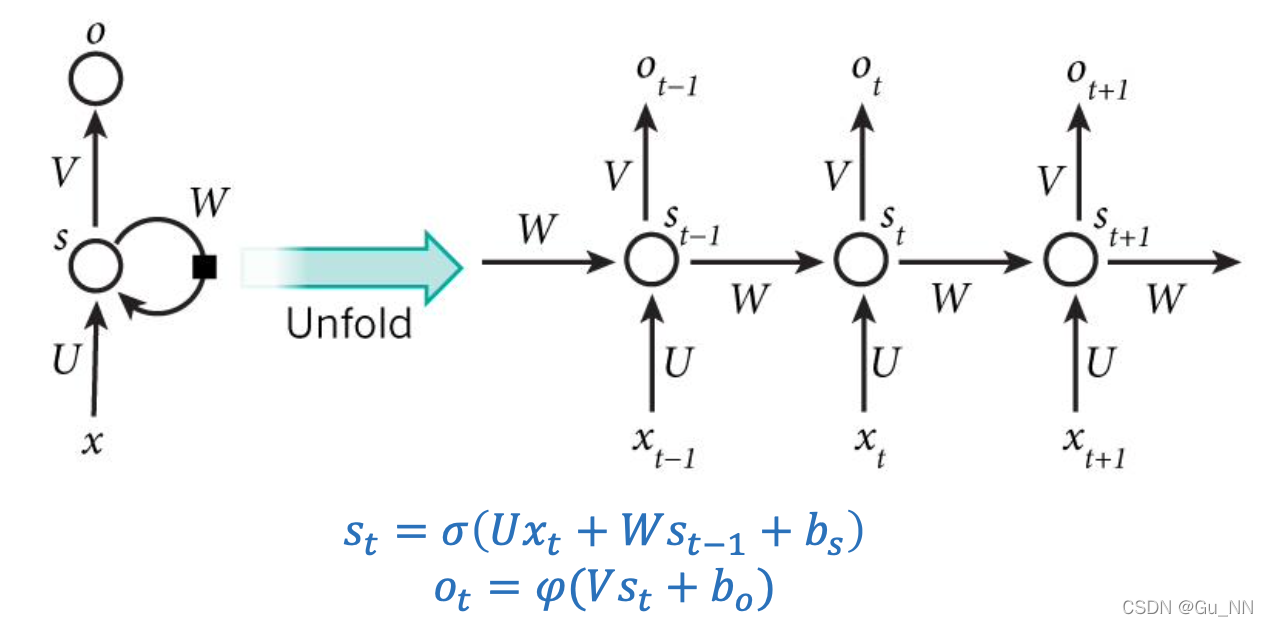
其中:
- x t x_t xt?:t时刻输入
- s t s_t st?:t时刻记忆(隐藏层)
- o t o_t ot?:t时刻输出
- U , W , V U,W,V U,W,V:连接权重
- b b b:偏置
- σ \sigma σ:激活函数,通常选tanh或sigmoid
- ψ \psi ψ:通常选softmax
基础RNN
Jordan Network
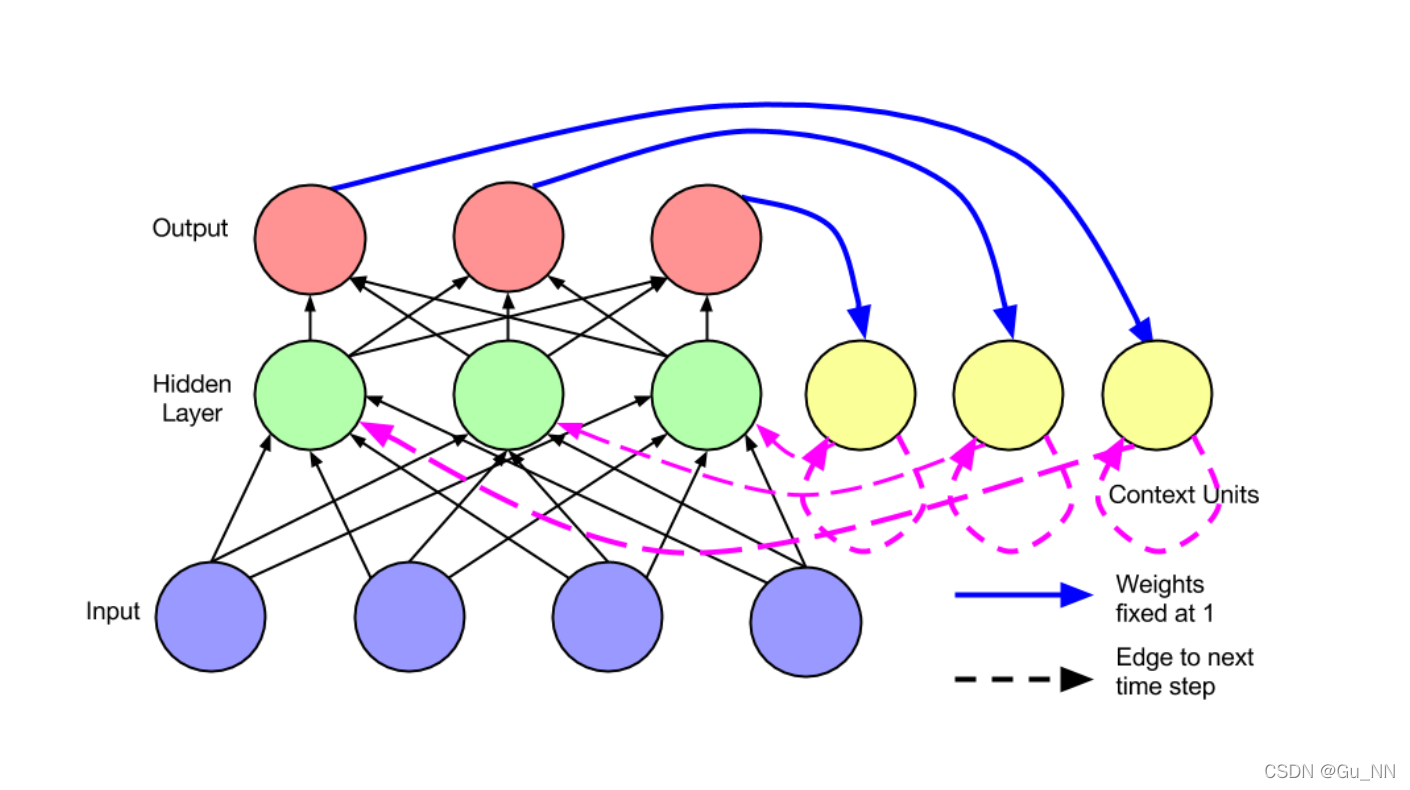
Elman Network
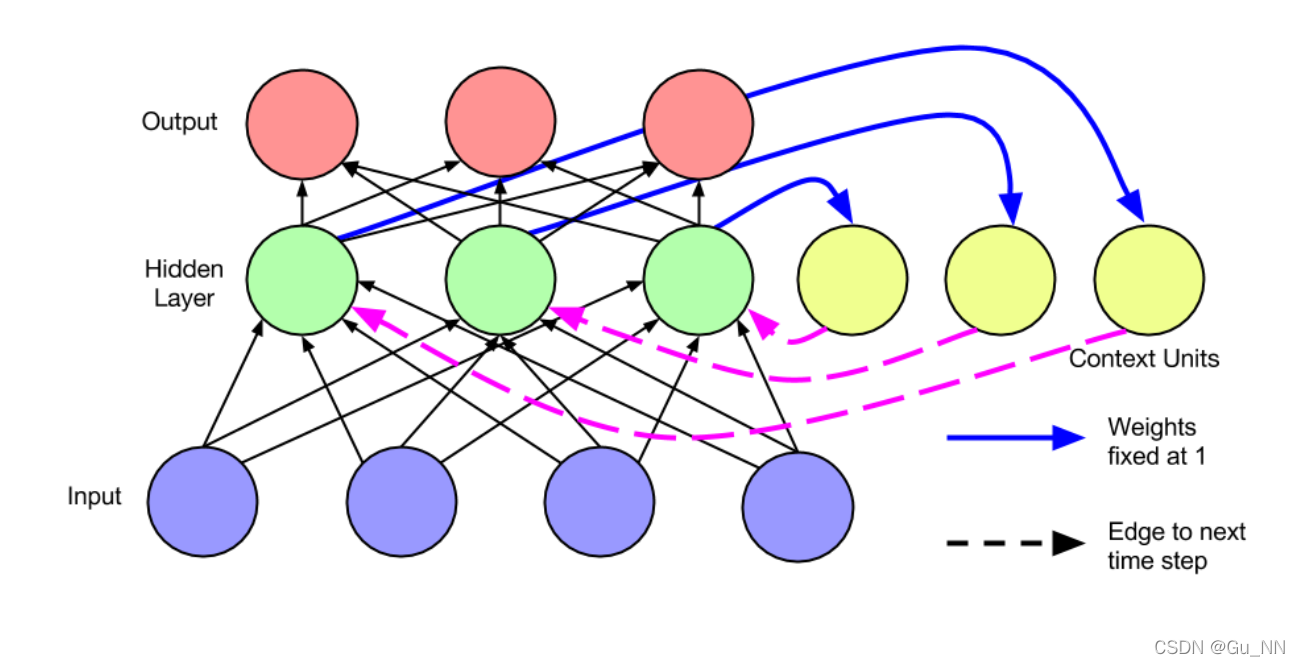
在Jordan network基础上简化:
- 隐藏层之间传递
- context unit无自循环
这个结构也是LSTM的基础结构
其他RNN结构
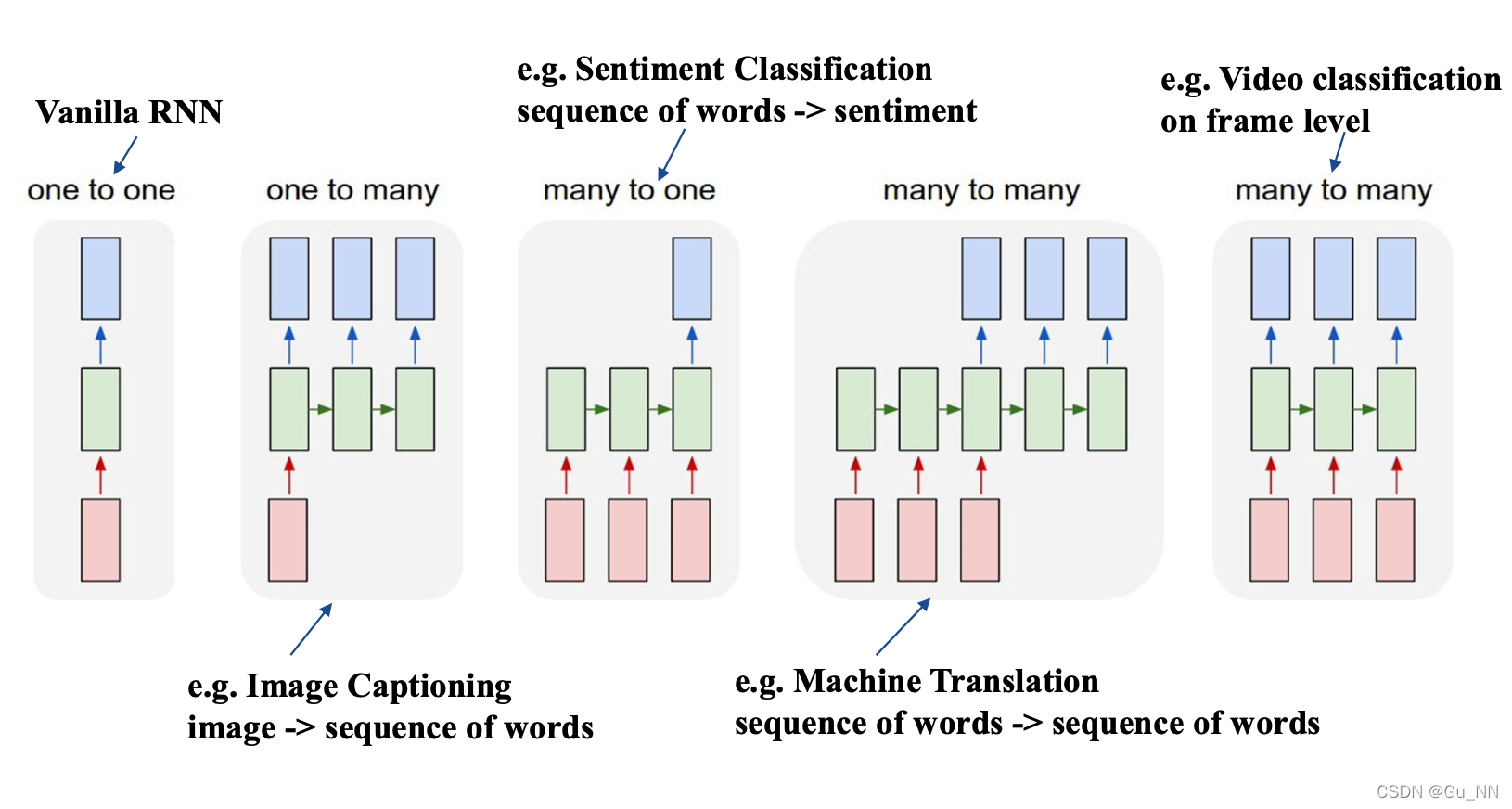
RNN训练方法——BPTT
BPTT(Error Back Propagation through Time)
- 思路:定义损失函数 Loss 来表示输出值
y
^
\hat y
y^?和真实标签
y
y
y的误差,通过链式法则自顶向下求得Loss对网络权重的偏导。沿梯度的反方向更新权重的值, 直到Loss收敛。
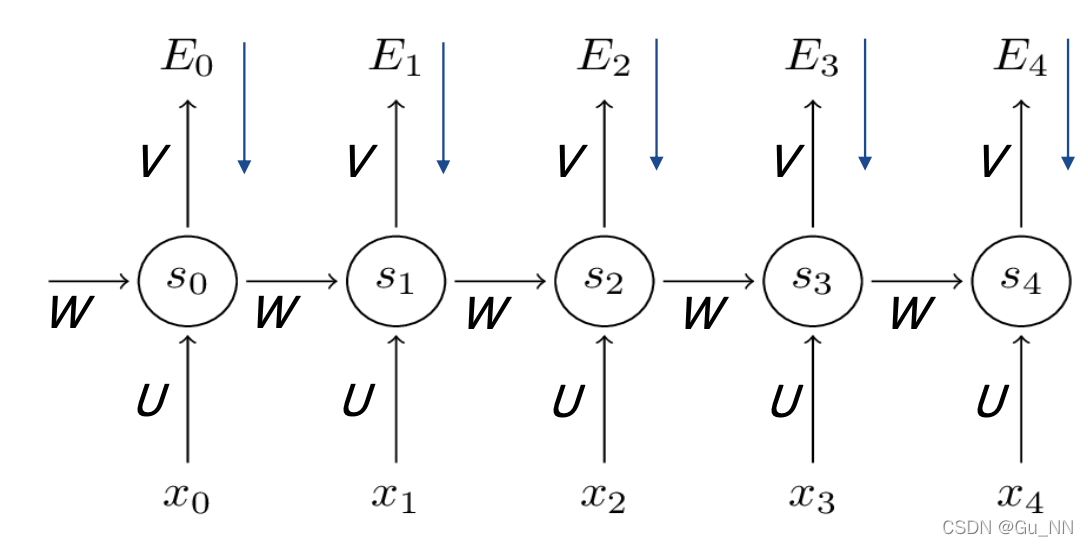
s t = t a n h ( U x t + W s t ? 1 ) s_t=tanh(Ux_t+Ws_{t?1}) st?=tanh(Uxt?+Wst?1?) y ^ t = s o f t m a x ( V s t ) \hat y_t=softmax(Vs_t) y^?t?=softmax(Vst?) L o s s = ∑ E t ( y t , y ^ t ) = ? ∑ y t l o g y ^ t Loss=\sum E_t(y_t,\hat y_t)=?\sum y_tlog\hat y_t Loss=∑Et?(yt?,y^?t?)=?∑yt?logy^?t? - 步骤:
- 计算损失函数
- 计算损失函数对V的偏导 ? E ? V = ∑ t ? E t ? V = ∑ t ? E j ? y ^ j ? y ^ j ? s j ? s j ? V \frac{\partial E}{\partial V}=\sum_t\frac{\partial E_t}{\partial V}=\sum_t \frac{\partial E_j}{\partial \hat y_j}\frac{\partial \hat y_j}{\partial s_j}\frac{\partial s_j}{\partial V} ?V?E?=t∑??V?Et??=t∑??y^?j??Ej???sj??y^?j???V?sj??
- 计算损失函数对W的偏导 ? E ? W = ∑ t ? E t ? W = ∑ t ∑ k = 0 j ? E j ? y ^ j ? y ^ j ? s j ( ∏ i = k + 1 j ? s i ? s i ? 1 ) ? s k ? W \frac{\partial E}{\partial W}=\sum_t\frac{\partial E_t}{\partial W}=\sum_t\sum_{k=0}^j \frac{\partial E_j}{\partial \hat y_j}\frac{\partial \hat y_j}{\partial s_j}(\prod_{i=k+1}^j\frac{\partial s_i}{\partial s_{i-1}})\frac{\partial s_k}{\partial W} ?W?E?=t∑??W?Et??=t∑?k=0∑j??y^?j??Ej???sj??y^?j??(i=k+1∏j??si?1??si??)?W?sk??
- 计算损失函数对U的偏导 ? E ? U = ∑ t ? E t ? U = ∑ t ∑ k = 0 j ? E j ? y ^ j ? y ^ j ? s j ? s j ? s k ? s k ? U \frac{\partial E}{\partial U}=\sum_t\frac{\partial E_t}{\partial U}=\sum_t \sum_{k=0}^j \frac{\partial E_j}{\partial \hat y_j}\frac{\partial \hat y_j}{\partial s_j}\frac{\partial s_j}{\partial s_k}\frac{\partial s_k}{\partial U} ?U?E?=t∑??U?Et??=t∑?k=0∑j??y^?j??Ej???sj??y^?j???sk??sj???U?sk??
- 反向更新权重
LSTM
梯度消失
- 原因:
- 反向传播算法采用梯度下降方法寻优
- 采用tanh激活函数
- 解决方法:
- 采用ReLU激活函数
- 引入“门”机制对细胞状态信息进行添加或删除(LSTM)
LSTM基本结构
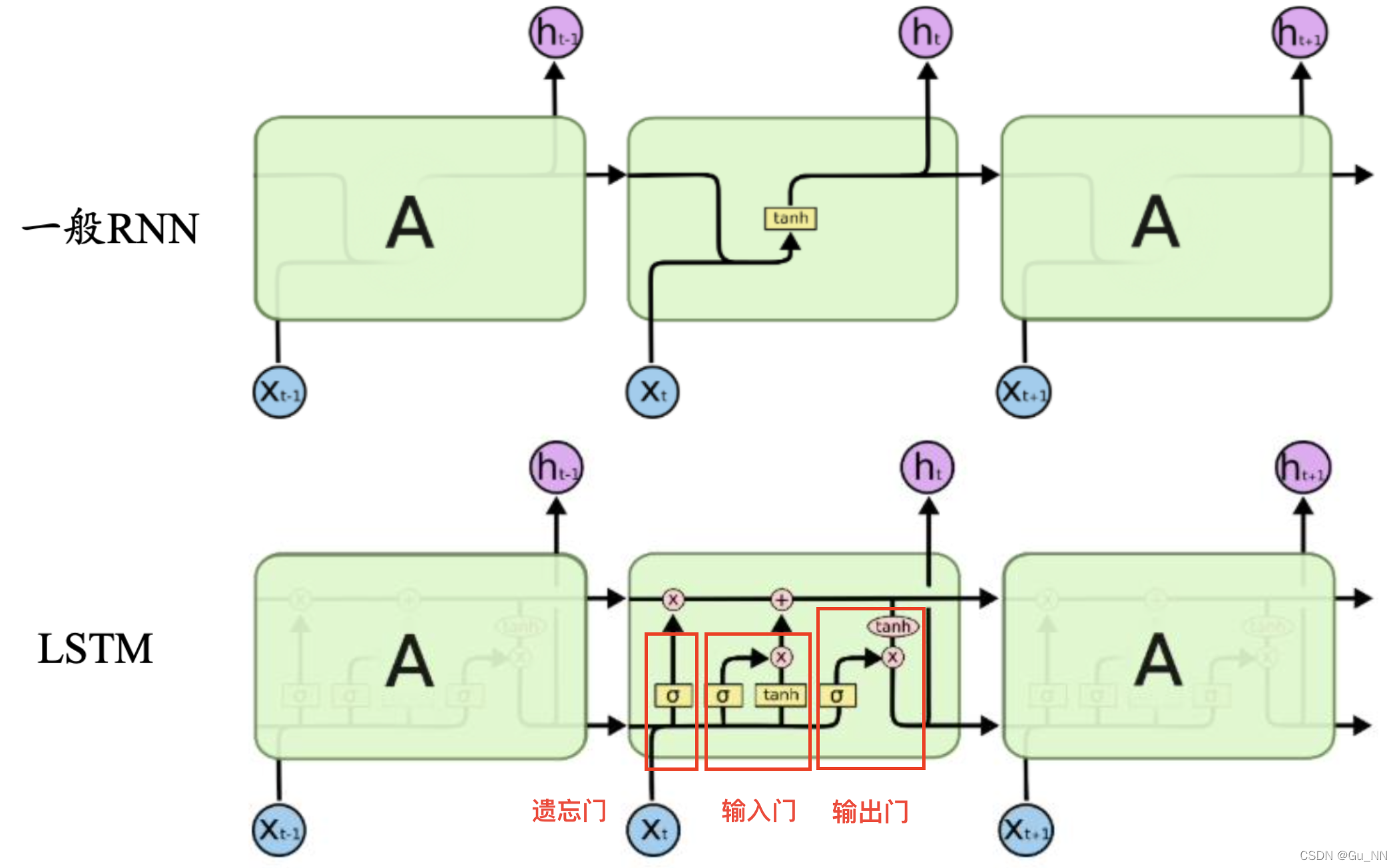
一个LSTM单元由输入门、输出门和遗忘门组成,三个门控制信息进出单元。 “门”机制由一个Sigmoid激活函数层和一个向量点乘操作组成。
- 遗忘门:控制遗忘程度 f t = σ ( W f ? [ h t ? 1 , x t ] + b f ) f_t=\sigma(W_f\cdot[h_{t?1},x_t]+b_f) ft?=σ(Wf??[ht?1?,xt?]+bf?)
- 输入门:控制信息接收程度 i t = σ ( W i ? [ h t ? 1 , x t ] + b i ) i_t=\sigma(W_i\cdot[h_{t?1},x_t]+b_i) it?=σ(Wi??[ht?1?,xt?]+bi?) C ~ t = t a n h ( W C ? [ h t ? 1 , x t ] + b C ) \tilde C_t = tanh(W_C\cdot[h_{t?1},x_t]+b_C) C~t?=tanh(WC??[ht?1?,xt?]+bC?)
- 输出门:控制输出认可程度 o t = σ ( W o ? [ h t ? 1 , x t ] + b o ) o_t=\sigma(W_o\cdot[h_{t?1},x_t]+b_o) ot?=σ(Wo??[ht?1?,xt?]+bo?)
状态更新: C t = f t ? C t ? 1 + i t ? C ~ t C_t=f_t?C_{t?1}+i_t? \tilde C_t Ct?=ft??Ct?1?+it??C~t? h t = o t ? t a n h ( C t ) h_t=o_t?tanh(C_t) ht?=ot??tanh(Ct?)
其他RNN
| 名称 | 时间 | 结构 | 特点 |
|---|---|---|---|
| Gated Recurrent Unit(GRU) | 2014 | 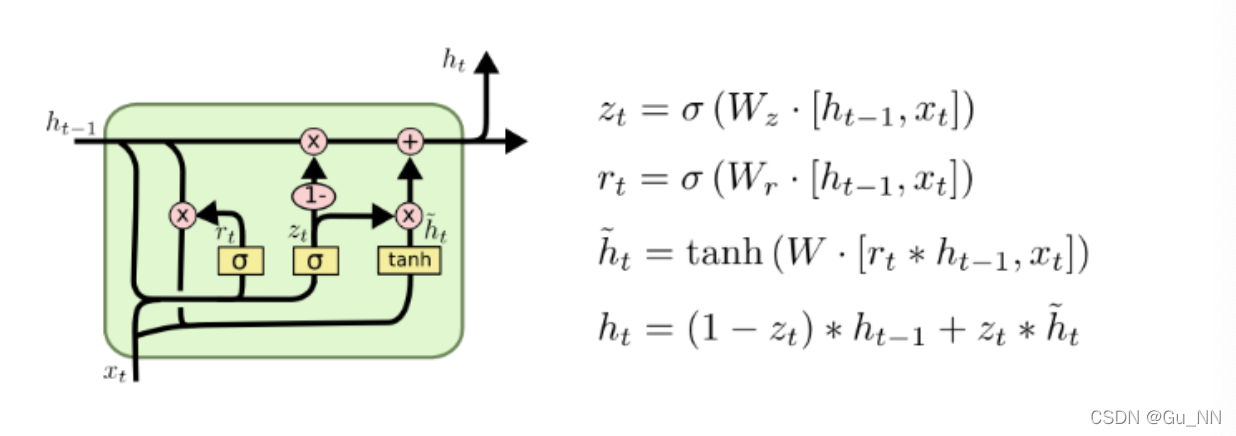 | 细胞结构本身和隐藏层重合; 仅有重置门和更新门 |
| Peephole LSTM | 2014 | 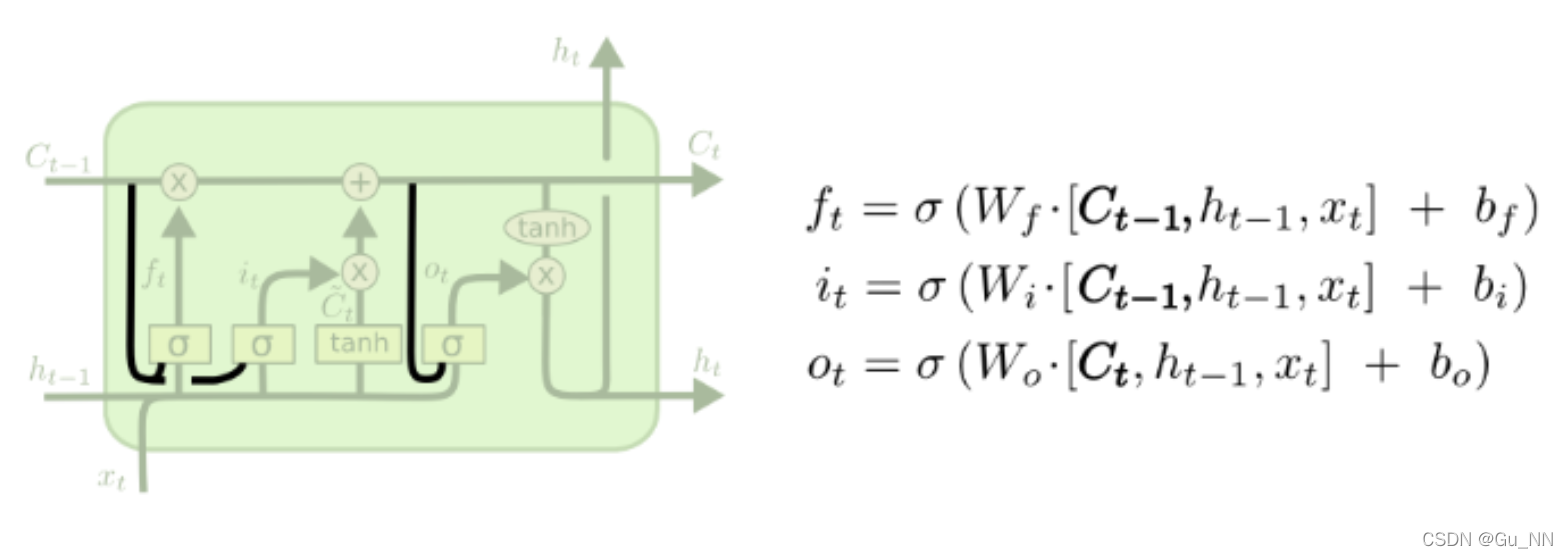 | 门层受细胞状态C、隐层信息h、输入状态x三个参数影响 |
| Bi-directional RNN(BRNN) | 1997 | 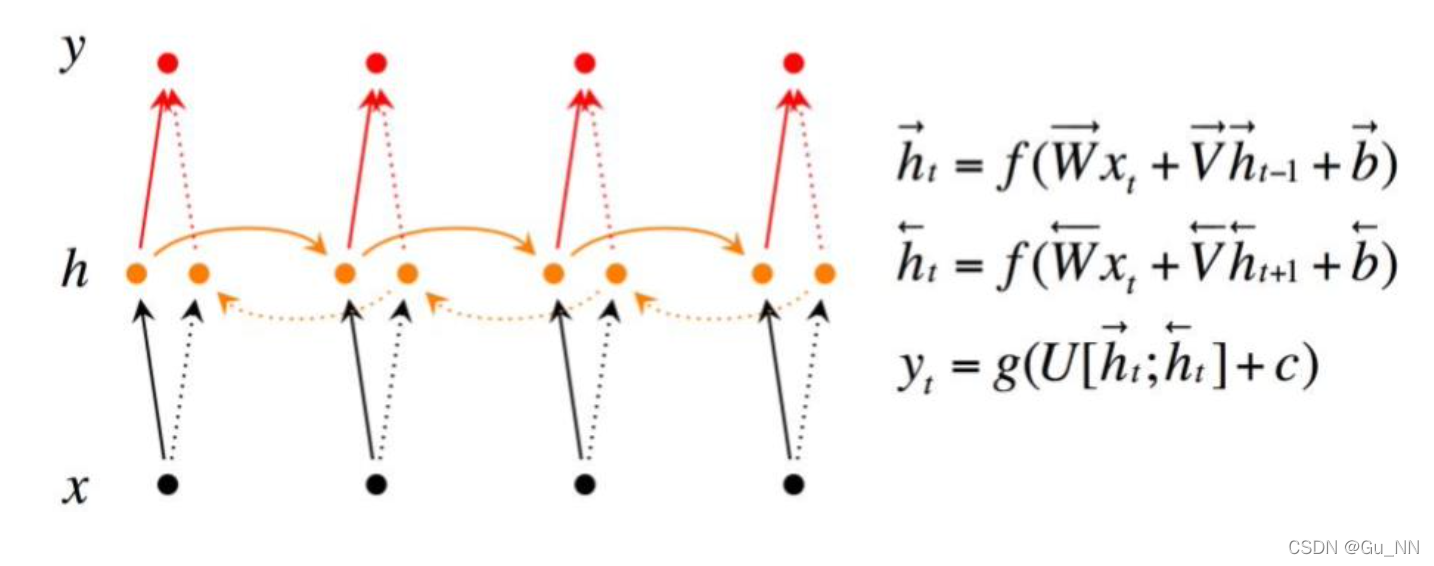 | 当前时间点受前后时间影响(上下文) |