循环神经网络的一般结构

如果
s
t
s_t
st? 的表达式中去除
W
s
t
?
1
Ws_{t-1}
Wst?1? 项,则循环神经网络退化成MLP。
循环神经网络本质上是在MLP基础上增加了 s t ? 1 s_{t-1} st?1?,使得网络与前一时刻的状态隐变量有关系,从而适用于处理有时序关系的信息。
最简单的RNN网络其实就是通过权重 W W W 来处理时序信息的。
梯度剪裁
- 迭代中计算 T T T 个时间步上的梯度,在反向传播过程中产生长度为 O ( T ) O(T) O(T) 的矩阵乘法链,导致数值不稳定。
- 梯度剪裁能够有效预防梯度爆炸,如果梯度长度超过 θ \theta θ, 则只取 θ \theta θ。
- 很多相同的数值相乘,会导致最终结果要么很小,产生梯度消失,要么很大,产生梯度爆炸。
RNN实现细节的理解
- num_steps 代表时间步,对于每一个时间步的输入,RNN 都会进行类似 MLP 的运算,所以 num_steps也可以看做等效于多个样本;
- RNN 一般的输出维度是 [批量大小×时间长度,隐藏层神经元数],因为实际上RNN网络等效于对 (批量大小×时间长度) 个样本进行了训练;
- 隐藏层权重每个时间步更新一次,而不是每个Batch更新一次,如果在一个Batch中有N个时间步,则会在这个Batch训练中更新N次隐藏层权重;
- num_steps 是时间长度,是输入样本序列的长度;Batch_size 代表一次训练同时训练的样本数量; num_steps 或者 time 类似于CNN网络中图片的大小;
- num_steps 代表对一个序列样本训练的次数,不等同于隐藏层的层数;
- RNN隐藏层神经元个数过少,是不太可能处理长时间序列,因为记不住;但是如果隐藏层神经元个数过多,又容易退化成 MLP,产生过拟合。
GRU
GRU 的结构比 LSTM 简单,但是两者的实际效果差不多。
关注序列时,不是每一个观测值都同等重要,只想记住相关的观察值,需要更新门进行关注,重置门进行遗忘。
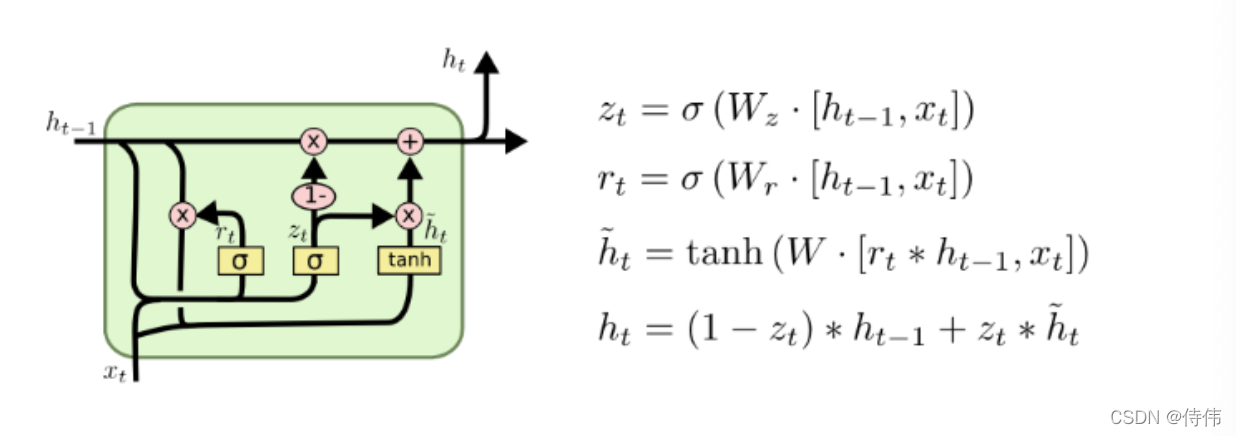
GRU 可学习的权重是 RNN 的3倍,因为多算了
W
z
W_z
Wz? 和
W
r
W_r
Wr? 的权重。
r
t
r_t
rt? 长度与
h
t
?
1
h_{t-1}
ht?1? 相同,用于决定候选隐藏状态
h
~
t
\widetilde{h}_{t}
h
t?保留多少
h
t
?
1
h_{t-1}
ht?1? 的信息。
z
t
z_t
zt? 长度与
h
t
?
1
h_{t-1}
ht?1? 相同,用于决定新的隐藏状态
h
t
h_t
ht? 采用多少候选隐藏状态
h
~
t
\widetilde{h}_{t}
h
t? 的信息进行更新。
当
z
t
z_t
zt? 为全1向量,
r
t
r_t
rt? 为全1向量,GRU就是原来的RNN模型。
总之
r
t
r_t
rt? 和
z
t
z_t
zt? 共同决定了新的隐藏状态
h
t
h_t
ht? 更受
h
t
?
1
h_{t-1}
ht?1? 影响,还是更受
x
t
x_t
xt? 的影响。
使用
r
t
r_t
rt? 的目的是可以控制候选隐藏状态
h
~
t
\widetilde{h}_{t}
h
t?受到
h
t
?
1
h_{t-1}
ht?1? 影响的程度。
使用
z
t
z_t
zt? 的目的是可以控制模型受到
x
t
x_t
xt? 影响的程度。
GRU、LSTM 等模型的数值稳定性比 RNN 要好,因为各种门都是使用 Sigmoid 函数,Sigmoid函数的输出值都在0到1之间,控制了数据的幅度。
传统的 RNN 网络由于容易梯度消失和爆炸,一般不再使用。通常说的 RNN网络 一般是指 GRU 或 LSTM,它们的计算量比 RNN 大一些,但是数值稳定性很好。
GRU 和 LSTM 的长度一般不超过100,如果长度更长的序列,可以考虑注意力机制。
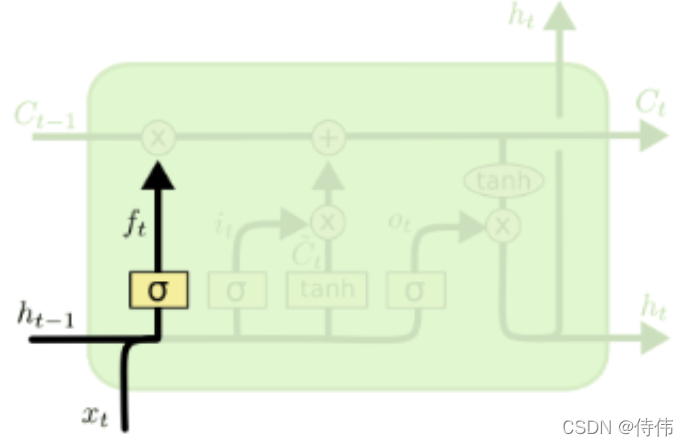
LSTM(长短期记忆网络)
- 忘记门:将值朝0减少
- 输入门:决定要不要忽略输入数据
- 输出门:决定要不要使用隐藏状态
遗忘门:LSTM通过遗忘门(forget gate)实现对细胞状态信息遗忘程度的控制,输出当前状态的遗忘权重,取决于
h
t
?
1
h_{t?1}
ht?1? 和
x
t
x_t
xt?.
f
t
=
σ
(
W
f
?
[
h
t
?
1
,
x
t
]
+
b
f
)
f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)
ft?=σ(Wf??[ht?1?,xt?]+bf?)
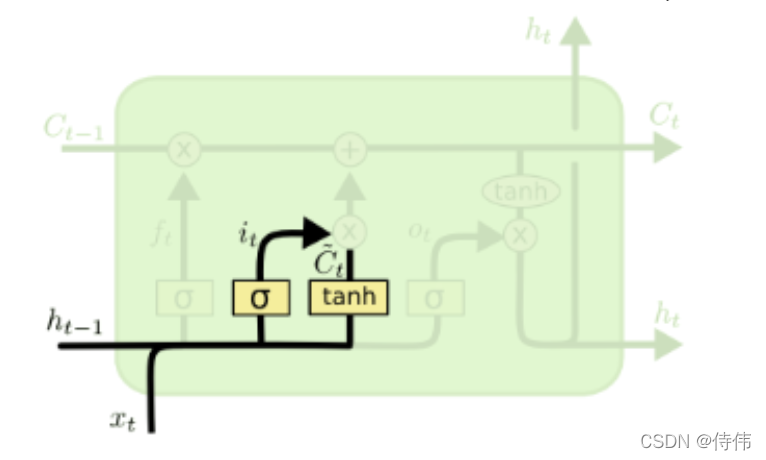
输入门:LSTM通过输入门(input gate)实现对细胞状态输入接收程度的控制,输出当前输入信息的接受权重,取决于
h
t
?
1
h_{t?1}
ht?1? 和
x
t
x_t
xt?.
i
t
=
σ
(
W
i
?
[
h
t
?
1
,
x
t
]
+
b
i
)
C
~
t
=
tanh
?
(
W
C
?
[
h
t
?
1
,
x
t
]
+
b
C
)
\begin{array}{c}i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right) \\ \tilde{C}_{t}=\tanh \left(W_{C} \cdot\left[h_{t-1}, x_{t}\right]+b_{C}\right)\end{array}
it?=σ(Wi??[ht?1?,xt?]+bi?)C~t?=tanh(WC??[ht?1?,xt?]+bC?)?
输出门:LSTM通过输出门(output gate)实现对细胞状态输出认可程度的控制,输出当前输出信息的认可权重,取决于
h
t
?
1
h_{t?1}
ht?1? 和
x
t
x_t
xt?.
o
t
=
σ
(
W
o
?
[
h
t
?
1
,
x
t
]
+
b
o
)
o_{t}=\sigma\left(W_{o} \cdot\left[h_{t-1}, x_{t}\right]+b_{o}\right)
ot?=σ(Wo??[ht?1?,xt?]+bo?)

状态更新:“门”机制对细胞状态信息进行添加或删除,由此实现长程记忆。
C
t
=
f
t
?
C
t
?
1
+
i
t
?
C
~
t
h
t
=
o
t
?
tanh
?
(
C
t
)
\begin{array}{c}C_{t}=f_{t} * C_{t-1}+i_{t} * \tilde{C}_{t} \\ h_{t}=o_{t} * \tanh \left(C_{t}\right)\end{array}
Ct?=ft??Ct?1?+it??C~t?ht?=ot??tanh(Ct?)?
LSTM 有两个状态单元
C
t
C_{t}
Ct? 和
h
t
h_{t}
ht? , 而 GRU 只有一个状态单元
h
t
h_{t}
ht?。
在LSTM里
f
t
f_{t}
ft? 和
i
t
i_{t}
it? 是相互独立的,增加了模型的自由度,不像 GRU 那样使用
z
t
z_t
zt? 和
1
?
z
t
1-z_t
1?zt? 以非此即彼的方式决定输出更依赖
h
t
h_{t}
ht? 还是
h
~
t
\widetilde{h}_{t}
h
t?。
LSTM 和 GRU 的设计思想是相似的,都是通过门函数来决定网络是更多的关注 h t ? 1 h_{t-1} ht?1?,还是更多的关注 x t x_t xt? 。最终的实现效果也是差不多的,所不同的是 LSTM 更复杂一些,所需要学习的参数更多,但是自由度也更大,更灵活一些。
参考资料
Datawhale 开源文档:https://github.com/liu-yang-maker/Easy-DL-Theory/tree/main/docs
B站视频《跟李沐学AI——动手学深度学习Pytorch版》:https://space.bilibili.com/1567748478/channel/seriesdetail?sid=358497
感谢Datawhale对开源学习的贡献!