[人工智能]文本表达论文-sentence embedding

1. BERT-avg

BERT-avg做法很简单，直接拿预训练后的模型来做相似度匹配，因为默认经过预训练后的模型含有先验知识，能够编码句子的语义

假如不经过fine-tuning，那就不能单纯把它们拼接起来作为输入，而是两个句子要分别输入BERT模型，通过词向量间接的获取句子向量，从而计算相似度，具体做法是：

• CLS token的的最后一层embedding计算余弦相似度
• 最后一层序列的输出(各词向量)求平均，再求余弦相似度[通常，做分类的时候，用max效果会较好，做语义的时候求mean效果较好]
• 把第一层和最后一层的输出加起来后做平均（有研究表明开始几层，主要蕴含词汇信息，靠任务的层主要蕴含语义信息，把它们拼接起来，让两种信息得到融合）

2. sentence BERT

论文：Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks-EMNLP 2019
代码：sentence bert github

BERT判断两个句子语义是否相似，需要将两个句子拼起来传入到model里，不适合多句子相似度判断。如果从句子数量为n的集合中，找出最近似的两个句子，则需要$\frac{n(n?1)}{2}$次比较，并且每次比较均需要传入到BERT模型中进行计算，开销非常大。
通过SBERT模型获取到的句子embedding，可以直接通过cos相似度计算两个句子的相似度，这样就大大减少了计算量

SBERT模型采用三种pooling策略：CLS、MEAN、MAX，默认SBERT采用MEAN pooling

2.1 目标函数构建

sentence bert的结构如图2.1所示，并使用了如下几种目标函数：

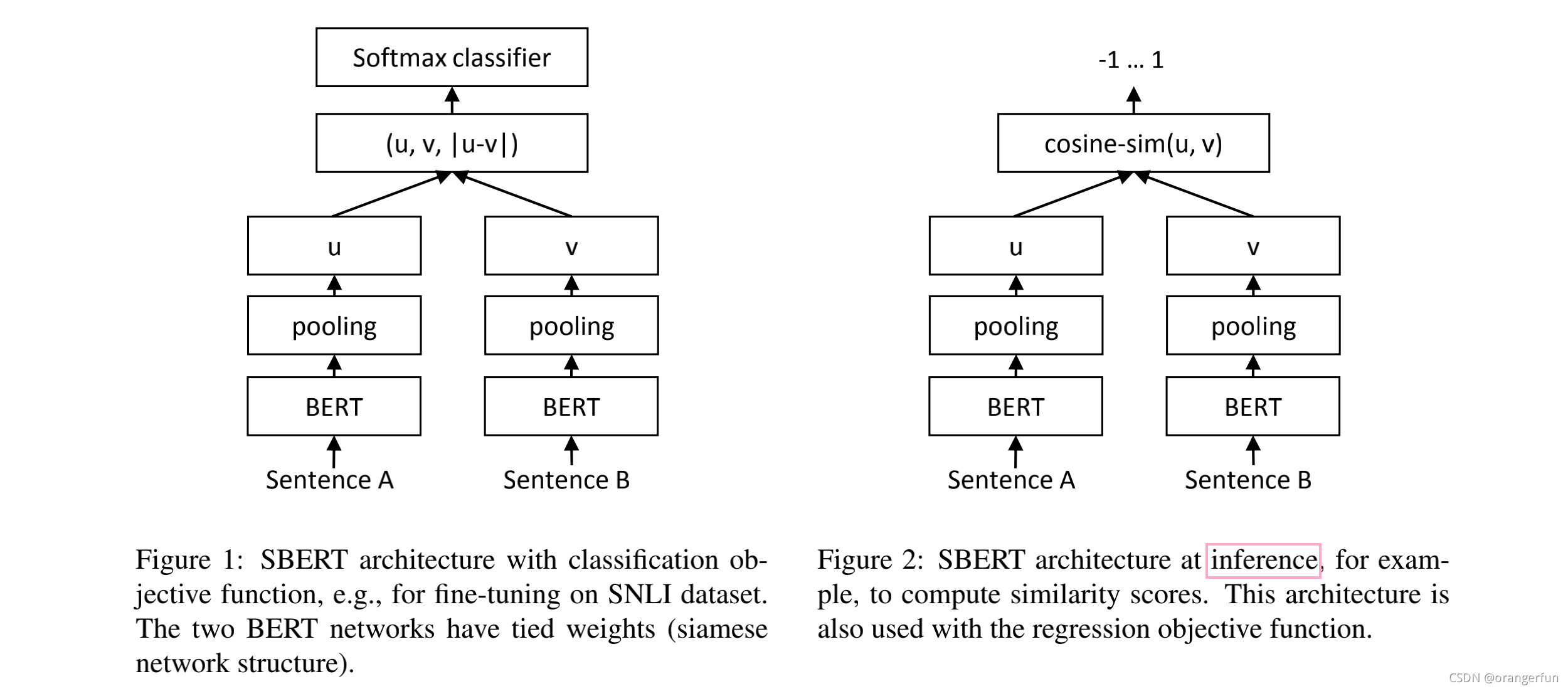
• 分类目标函数
  将句子向量 $u,v,|u?v|$ 拼接起来并乘以训练得到的权重$w_t\in R^{3n\times k}$

$$o=\mathrm{softmax}\left(W_t(u,v,|u?v|)\right)$$

其中：n表示句子向量的维度，k表示标签的个数，通过交叉熵损失进行优化

• 回归目标函数
  使用cos函数计算两个句子embeding的相似度，使用均方误差作为损失函数
• 三元组目标函数
  给定一个句子$a$，一个正例句子$p$，一个负例句子$n$。triplet loss微调网络使得句子$a$与句子$p$的距离比$a$与句子$n$的距离小，即句子$a$的sentence embedding 更接近句子$p$的sentence embedding

$$\max \left(\Vert s_a?s_p\Vert ?\Vert s_a?s_n\Vert +?,0\right)$$

其中，$s_x$表示x的embedding，$?$参数的目的是为了保证$s_p$到$s_a$的距离至少比$s_a$到$s_n$的距离近$?$，在实验中，使用欧式距离并设置? = 1

3. BERT-FLOW

论文：On the Sentence Embeddings from Pre-trained Language Models
代码: bert flow coding github

直接使用bert获取句向量的缺点

论文1和论文2证明了 transformer 模型出来的向量表达（如 BERT、GPT2）会产生各向异性，具体表现是向量分布不均匀，低频词分布稀疏距离原点较远，高频词分布紧密，距离原点较近，如图1所示。

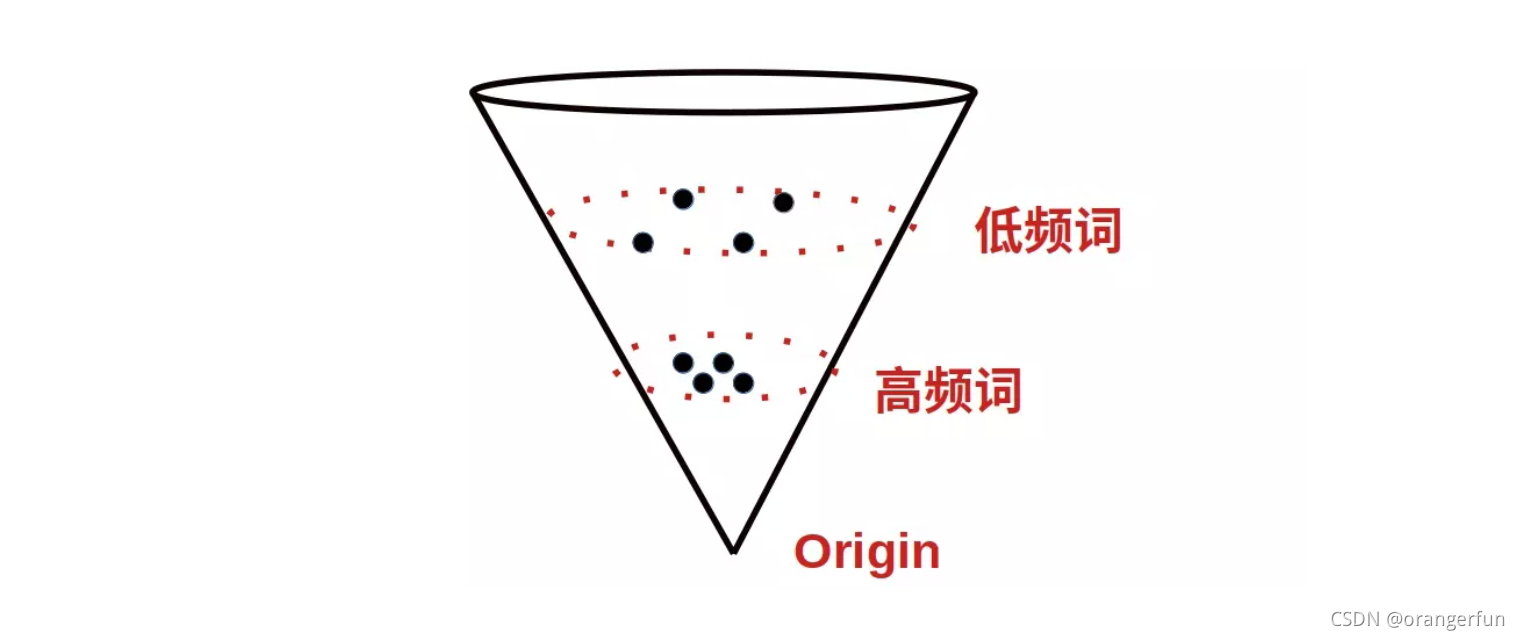
向量值受句子中词在所有训练语料里的词频影响，导致高频词编码的句向量距离更近，更集中在原点附近，导致即使一个高频词和一个低频词的语义是等价的，但词频的差异也会带来很大的距离偏差，从而词向量的距离就不能很好地代表语义相关性，和人判断句子的语义不受词频影响也不符合。

On the Sentence Embeddings from Pre-trained Language Models论文也通过试验验证了上述问题：

文中通过度量BERT词向量表示与原点 $l_2$ 距离的均值得到下表

文中度量了词向量空间中与K近邻单词的 $l_2$ 距离的均值。我们可以看到高频词分布更集中，而低频词分布则偏向稀疏。

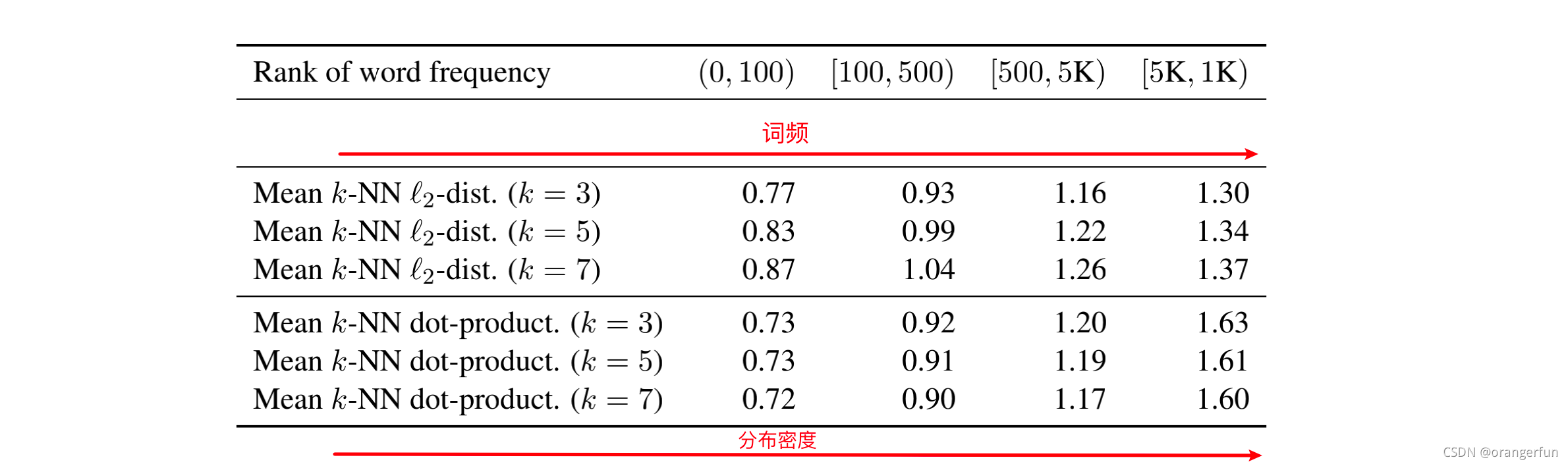
针对以上问题，作者提出了一种将BERT embedding空间映射到一个标准高斯隐空间的方法，并称之为BERT-flow

BERT-flow 采用一种流式可逆变换：
z服从标准高斯分布(先验分布)：$f_{?}$ 是 $z$ 到 $u$ 的可逆变换
$$\begin{gathered} \mathbf{z}～p_{\mathcal{Z}}(\mathbf{z}), \\ \mathbf{u}=f_{?}(\mathbf{z}) \end{gathered}$$

那么根据概率密度函数的变量代换定理，$u$的概率密度函数：
$$p_{\mathcal{U}}(\mathbf{u})=p_{\mathcal{Z}}\left(f_{?}^{?1}(\mathbf{u})\right)\left|\det \frac{?f_{?}^{?1}(\mathbf{u})}{?\mathbf{u}}\right|$$
注意概率密度函数的变量代换并不是简单地将z替换为f(x)就行了，还多出了一个“雅可比行列式”的绝对值

最后的优化目标是最大化$p_{\mathcal{U}}$
$$\begin{array}{rl}\underset{?}{\max }& {\mathbb{E}}_{\mathbf{u}=\mathrm{BERT}(\text{?sentence?})\text{?sentence?}\mathcal{D}}\\ & \log p_{\mathcal{Z}}\left(f_{?}^{?1}(\mathbf{u})\right)+\log \left|\det \frac{?f_{?}^{?1}(\mathbf{u})}{?\mathbf{u}}\right|\end{array}$$
详细参考：苏剑林-细水长flow之NICE：流模型的基本概念与实现

4. 带白化处理的BERT-whitening

论文：Whitening Sentence Representations for Better Semantics and Faster Retrieval
代码：bert whitening coding github

基本思想与BERT-FLOW相同，将BERT embedding空间映射到一个标准高斯隐空间。但是BERT-FLOW的flow模型较为复杂，该论文提出使用线性变换即可实现flow模型的效果。

标准正态分布的均值是$\mu =0$，协方差矩阵为单位矩阵，那么我们的目标就是把句向量的均值变换为$\mu =0$，协方差矩阵变换为单位矩阵。假设行向量集合为 { x i } i = 1 N \{x_i\}_{i=1}^{N} {xi?}i=1N?，执行以下变换：
$${\tilde{\mathbf{x}}}_i=\left({\mathbf{x}}_i?\mathbf{\mu }\right)\mathbf{W}$$

从而使得 { x ~ i } i = 1 N \left\{\tilde{\boldsymbol{x}}_{i}\right\}_{i=1}^{N} {x~i?}i=1N?的均值为$\mu$，协方差矩阵为单位阵

均值$\mu$求法比较简单$\mathbf{\mu }=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{x}}_i$。下面重点介绍$W$矩阵的求解：

将原始数据的协方差矩阵记为

$$\mathbf{\Sigma }=\frac{1}{N}\sum _{i=1}^N{\left({\mathbf{x}}_i?\mathbf{\mu }\right)}^{?}\left({\mathbf{x}}_i?\mathbf{\mu }\right)$$

变换后的数据协方差矩阵为

$$\tilde{\mathbf{\Sigma }}=\frac{1}{N}\sum _{i=1}^N{\left({\tilde{\mathbf{x}}}_i?\tilde{\mathbf{\mu }}\right)}^{?}\left({\tilde{\mathbf{x}}}_i?\tilde{\mathbf{\mu }}\right)=\frac{1}{N}\sum _{i=1}^N{\tilde{\mathbf{x}}}_i^{?}{\tilde{\mathbf{x}}}_i={\mathbf{W}}^{?}\mathbf{\Sigma }\mathbf{W}$$

那么，实际上要解方程

$${\mathbf{W}}^{?}\mathbf{\Sigma }\mathbf{W}=\mathbf{I}?\mathbf{\Sigma }={\left({\mathbf{W}}^{?}\right)}^{?1}{\mathbf{W}}^{?1}={\left({\mathbf{W}}^{?1}\right)}^{?}{\mathbf{W}}^{?1}$$

协方差矩阵$\sum$是一个半正定对称矩阵，半正定对称矩阵都具有如下形式的SVD分解

$$\mathbf{\Sigma }=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{?}$$

其中$U$是一个正交矩阵，而$\Lambda$是一个对角阵，并且对角线元素都是正的，因此可以求得：

$$\mathbf{W}=\mathbf{U}\sqrt{{\mathbf{\Lambda }}^{?1}}$$

算法流程如下：

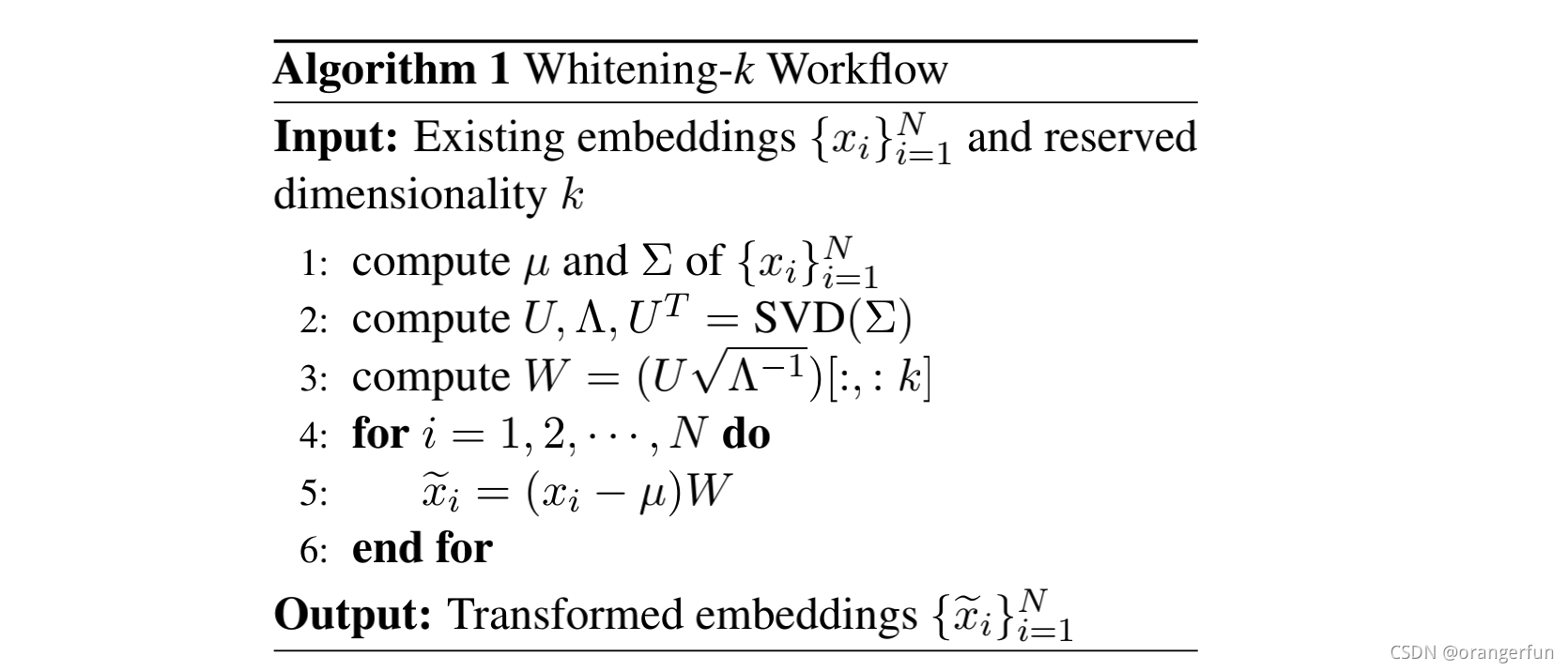
把当前任务的语料，分别一句句地输入到预训练模型中得到各自的embedding，然后对embeddings做特征值分解，得到变换矩阵，然后存起来。应用时，输入新的句子，把它们输入预训练模型，得到句子embedding，再用存起来的变换矩阵u和W做变换，这时候得到的embedding就是标准正交基表示的embedding

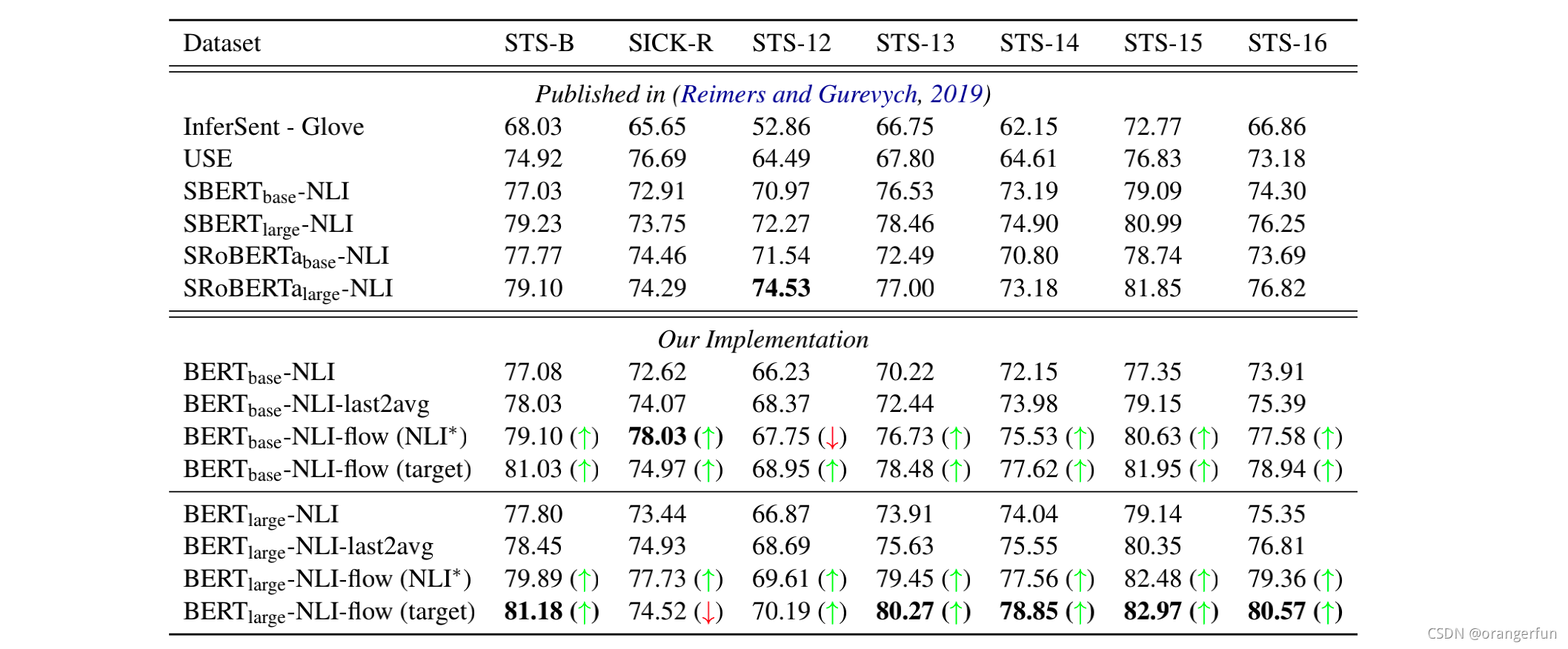
试验结果如下：

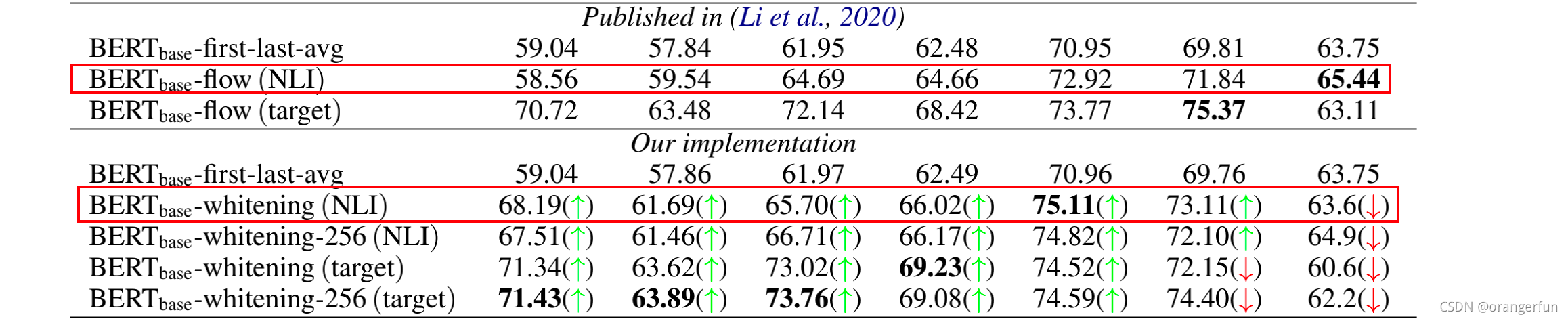
5. 对比学习的SimCSE

论文: SimCSE: Simple Contrastive Learning of Sentence Embeddings
代码; simcse coding github

SimCSE的核心思想是对比学习，上面提到的BERT-avg和BERT-whitening都是无监督的方法，这里提到的SimCSE有无监督和有监督两种模式，其中的无监督模式是当前无监督的SOTA方法。

什么是对比学习？
对比学习的思想是拉近相似的样本，推开不相似的样本，一种常用的对比损失是基于批内负样本的交叉熵损失。假设有一个数据集$\mathcal{D}={\left\{\left(x_i,x_i^{+}\right)\right\}}_{i=1}^m$ 其中$x_i$和$x_i^{+}$是语义相关的，则在大小为$N$的mini batch内，$\mathcal{D}={\left\{\left(x_i,x_i^{+}\right)\right\}}_{i=1}^m$ 的训练目标为

$${?}_i=?\log \frac{e^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_i^{+}\right)/\tau }}{{\sum }_{j=1}^N{e}^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_j^{+}\right)/\tau }}$$

其中，$\mathrm{sim}\left({\mathbf{h}}_1,{\mathbf{h}}_2\right)=\frac{{\mathbf{h}}_1^T{\mathbf{h}}_2}{\Vert {\mathbf{h}}_1\Vert ?\Vert {\mathbf{h}}_2\Vert }$， $h_i$和$h_i^{+}$是$x_i$和$x_i^{+}$的编码表示，$\tau$为softmax的温度超参。

5.1 构造正实例

使用对比损失最关键的问题是如何构造$(x_i,x_i^{+})$，对比学习最早起源于CV领域的原因之一就是图像的$x_i$非常容易构造，裁剪、翻转、扭曲和旋转都不影响人对图像语义的理解，而结构高度离散的自然语言则很难构造语义一致的$x_i^{+}$，前人采用了一些数据增强方法来构造$x_i^{+}$，比如同义词替换，删除不重要的单词，语序重排等，但这些方法都是离散的操作，很难把控，容易引入负面噪声，模型也很难通过对比学习的方式从这样的样本中捕捉到语义信息，性能提升有限。

5.2 对比学习评价指标

对比学习的目标是从数据中学习到一个优质的语义表示空间，衡量对比学习质量有两个指标：alignment 和 uniformity

• Alignment：评估的是相似的样本向量间的一致性（即计算$x_i$和$x_i^{+}$的平均距离），也就是说相似样本间有相似的feature，差距应该小。

$${?}_{\text{align?}}?\underset{\left(x,x^{+}\right)～p_{\text{pos?}}}{E}{\Vert f(x)?f\left(x^{+}\right)\Vert }^2$$

• uniformity：评估的是向量整体分布的均匀程度，也就是说向量应该均匀分布在球面上，不应该出现 BERT 那种分布不均（高频词分布集中紧凑，低频词稀疏），其中$P_{data}$代表数据分布

$${?}_{\text{uniform?}}?\log \underset{x,y～Pdata}{E}{e}^{?2\Vert f(x)?f(y){\Vert }^2}$$

我们希望这两个指标都尽可能低，也就是一方面希望正样本要挨得足够近，另一方面语义向量要尽可能地均匀分布在超球面上，因为均匀分布信息熵最高，分布越均匀则保留的信息越多，“拉近正样本，推开负样本”实际上就是在优化这两个指标。

5.3 Unsupervised SimCSE

将一个句子输入 encoder 两次，由于 bert encoder 是一个随机 dropout mask encoder,因此输入一个句子两次会得到两个不同的 embedding，产生的这两个 embedding 作为训练中相互对比的正样本，同一个 batch 中其他句子产生的 embedding 则作为负样本，以此来构造一个对比学习的无监督训练。那么训练目标为：

$${?}_i=?\log \frac{e^{\mathrm{sim}\left({\mathbf{h}}_i^{z_i},{\mathbf{h}}_i^{z_i^{{}^{\prime }}}\right)/\tau }}{{\sum }_{j=1}^N{e}^{\mathrm{sim}\left({\mathbf{h}}_i^{z_i},{\mathbf{h}}_j^{z_j^{{}^{\prime }}}\right)/\tau }}$$

原样本和生成的正样本的语义是完全一致，只是生成的embedding不同

5.4 Supervised SimCSE

使用了NLI 数据集SNLI，每一条原始数据( premise)有对应的一个与之完全同语义的句子(entailment)和一个完全不同语义的句子(contradiction)以及一个中性句子(neural)， 数据集中的entailment作为正样本，conradiction作为负样本，加上原样本premise一起组合为$(x_i,x_i^{+},x_i^{?})$， 并将损失函数改进为

$$l_i=?\log \frac{e^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_i^{+}\right)/\tau }}{{\sum }_{j=1}^N\left(e^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_j^{+}\right)/\tau }+e^{\mathrm{sim}\left({\mathbf{h}}_i,{\mathbf{h}}_j^{?}\right)/\tau }\right)}$$

5.5 对比学习也可解决各向异性

当负样本数量趋于无穷大时，对比学习的训练目标可以渐近表示为：

$$?\frac{1}{\tau }\underset{\left(x,x^{+}\right)～p_{\mathrm{p}\mathrm{o}\mathrm{s}}}{E}\left[f(x{)}^{?}f\left(x^{+}\right)\right]+\underset{x～p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}}{E}\left[\log \underset{x^{?}～p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}}{E}\left[e^{f(x{)}^{?}f\left(x^{?}\right)/\tau }\right]\right]$$

其中第一项表示拉近正样本，第二项表示推开负样本

借助Jensen不等式进一步推导第二项的下界

$$\begin{array}{rl}\underset{x～p_{\text{data?}}}{E}\left[{\log }_{x^{?}～p_{\text{data?}}}\left[e^{f(x{)}^{?}f\left(x^{?}\right)/\tau }\right]\right]& =\frac{1}{m}\sum _{i=1}^m\log \left(\frac{1}{m}\sum _{j=1}^m{e}^{{\mathbf{h}}_i^{?}{\mathbf{h}}_j/\tau }\right)\\ & \ge \frac{1}{\tau m^2}\sum _{i=1}^m\sum _{j=1}^m{\mathbf{h}}_i^{?}{\mathbf{h}}_j=sum(W^{T}W)\end{array}$$

根据Merikoski (1984)的结论，$sum(W^{T}W)$是$W^{T}W$最大特征值的上界，因此，当我们最小化损失的第二项时，我们其实是在间接最小化$W^{T}W$的最大特征值，也就是隐式地压平了嵌入空间的奇异谱

对比学习可以潜在地解决表示退化的问题，提升表示向量分布的uniformity，之前的BERT-flow和BERT-whitening仅仅致力于寻找各向同性的表示分布，而在优化对比损失时，对比损失的第二项能够达到同样的规整分布的效果，同时，对比损失的第一项还能确保正样本的对齐，这两项起到了相互制约和促进的作用，最终使得SimCSE在BERT和BERT-flow之间找到了平衡点

5.6 试验结果

使用bert的cls向量作为句子向量

如图所示，可以发现性能更优的模型通常有着更好的alignment和uniformity，BERT虽然有很好的alignment，但uniformity太差，而基于后处理的BERT-flow和BERT-whitening又恰恰走向了另一个极端，本文提出的SimCSE则是对这两个指标的一个很好的平衡，加入监督训练后，SimCSE的两个指标会同时提升

5.7 论文中的一些细节

无监督训练时，除了用dropout生成语义相同的句子对，论文里还采用过：

• Crop：随机删掉一段span
• Word deletion：随机删除词
• MLM：用BERT预训练任务之一，用一些随机token或【MASK】token代替原序列的某些token

最后发现dropout效果是最好

6. 参考

[1]. align&uniform: Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere
[2]. 文本表达进击：从BERT-flow到BERT-whitening、SimCSE
[3]. 知乎-SimCSE: Simple Contrastive Learning of Sentence Embeddings
[4]. 细节满满！理解对比学习和SimCSE，就看这6个知识点
[5]. 中文任务还是SOTA吗？我们给SimCSE补充了一些实验