系列文章目录
数字信号处理(DSP:Digital Signal Process)是电子通信领域非常重要的研究方向,博主汇总了数字信号处理(DSP)中常用的经典案例分析,主要基于算法分析、MATLAB程序实现、信号图像显示,对数字信号处理的实际应用进行详细分析。第一篇 常见离散信号的MATLAB产生和图形显示
常见离散信号的MATLAB产生和图形显示
第二篇 零极点分布对系统频率响应的影响
零极点分布对系统频率响应的影响
第三篇 基于matlab实现信号的线性卷积与循环卷积
基于matlab实现信号的线性卷积与循环卷积
一、研究目的
1.进一步掌握线性卷积的计算机编程方法,利用卷积的方法观察系统响应的时域特性。
2.掌握循环卷积的计算机编程方法,并比较与线性卷积的差别,验证二者之间的关系。利用循环卷积的方法观察、分析系统响应的时域特性。
二、原理分析
1.线性卷积
线性时不变系统(Linear Time-Invariant System, or L. T. I系统)输入、输出间的关系为:当系统输入序列为x(n) ,系统的单位脉冲响应为h(n),输出序列为y(n),则系统输出为:
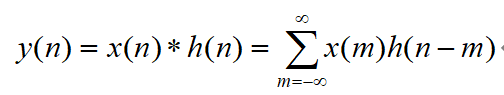
上式称为线性卷积
2.循环卷积

3.两个有限长序列的线性卷积
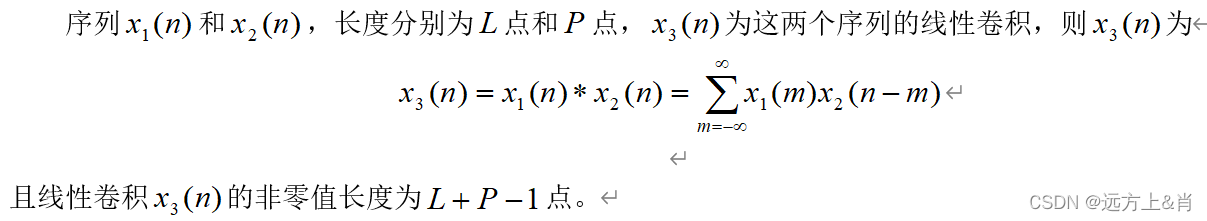
4.循环卷积与线性卷积的关系

三、实验内容
已知长为4的两个有限长序列
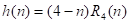
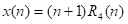
- 利用MATLAB的conv()函数求线性卷积 ,并绘出图形。
- 利用MATLAB构建的循环卷积函数计算下述4种情况下x(n)和h(n) 循环卷积,并绘出图形。
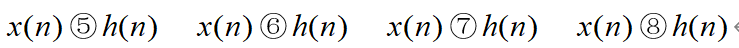
- 调用fft()函数利用循环卷积定理计算下述4种情况下x(n)和h(n) 循环卷积,并绘出图形。
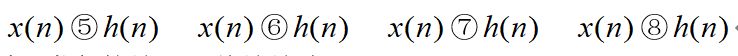
四、实验代码(matlab)及结果图像
- conv函数
function y=circonv(x1,x2)
%这里的两个序列x1,x2都是假设从1开始,一直到N;
xn2=[x2(1),fliplr(x2)];
xn2(length(xn2))=[];
C=xn2;
R=x2;
M=toeplitz(C,R);
y=x1*(M);
end
- 线性卷积
%%4(1)
nx=0:3;
x=(nx+1);
nh=0:3;
h=4-nh;
ny=0:6;
y=conv(x,h);
figure;
subplot(3,1,1);
stem(nx,x);
xlabel('n');ylabel('x(n)');
subplot(3,1,2);
stem(nh,h);
xlabel('n');ylabel('h(n)');
subplot(313);
stem(ny,y);
xlabel('n');ylabel('y(n)');
title('线性卷积');
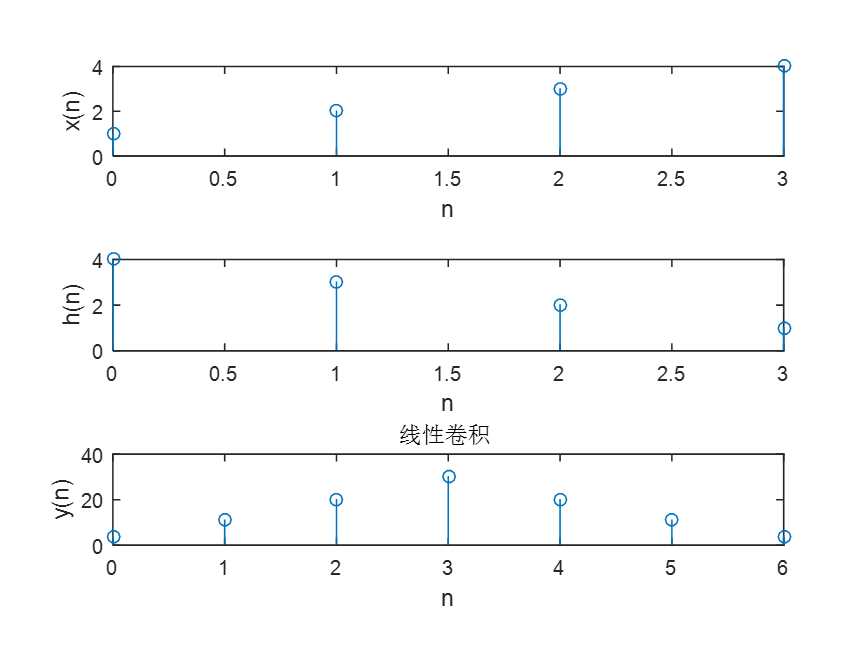
- 循环卷积
nx=0:3;
x=(nx+1);
nh=0:3;
h=4-nh;
yc5=circonv([x,0],[h,0]);
yc6=circonv([x,0,0],[h,0,0]);
yc7=circonv([x,0,0,0],[h,0,0,0]);
yc8=circonv([x,0,0,0,0],[h,0,0,0,0]);
figure;
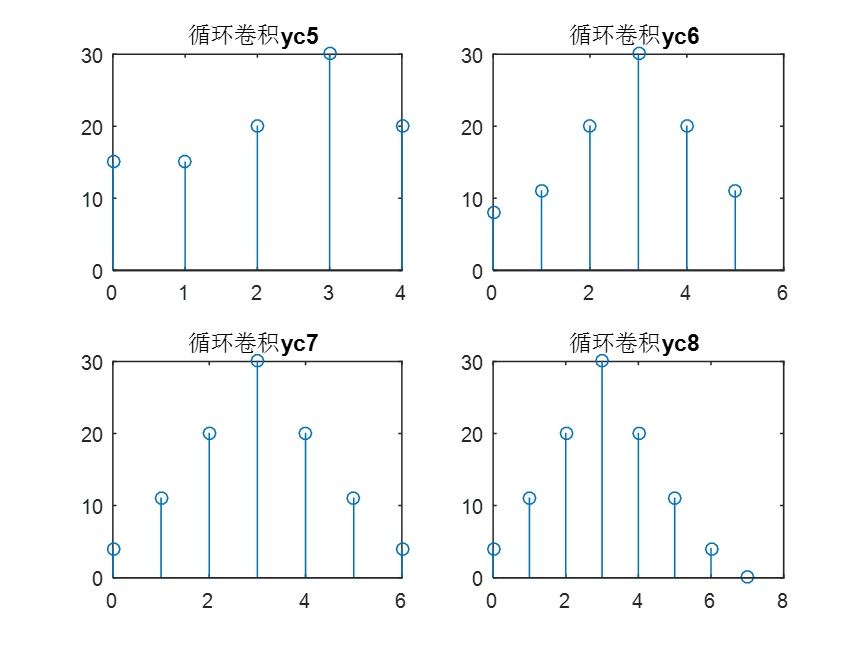
subplot(2,2,1);stem(0:4,yc5); title('循环卷积yc5');
subplot(2,2,2);stem(0:5,yc6); title('循环卷积yc6');
subplot(2,2,3);stem(0:6,yc7); title('循环卷积yc7');
subplot(2,2,4);stem(0:7,yc8); title('循环卷积yc8');
- FFT
nx=0:3;
x=(nx+1);
nh=0:3;
h=4-nh;
yc51=ifft(fft(x,5).*fft(h,5));
yc61=ifft(fft(x,6).*fft(h,6));
yc71=ifft(fft(x,7).*fft(h,7));
yc81=ifft(fft(x,8).*fft(h,8));
figure;
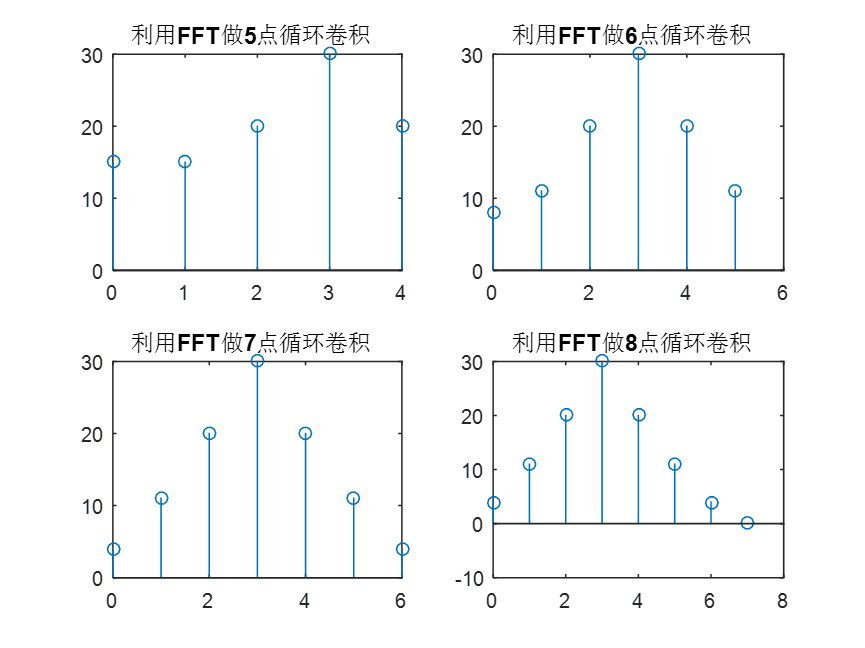
subplot(2,2,1);stem(0:4,yc51);title('利用FFT做5点循环卷积');
subplot(2,2,2);stem(0:5,yc61);title('利用FFT做6点循环卷积');
subplot(2,2,3);stem(0:6,yc71);title('利用FFT做7点循环卷积');
subplot(2,2,4);stem(0:7,yc81);title('利用FFT做8点循环卷积');