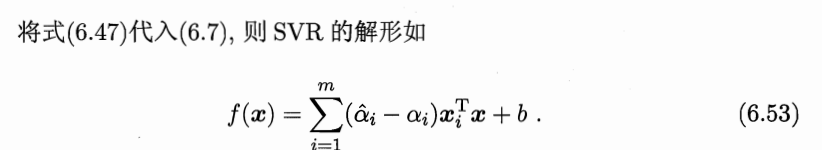支持向量机
二分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面。
支持向量机
从集合几何角度来看,对于线性可分数据集,支持向量机就是找距离正负样本都最远的那个超平面。
相比于感知机:其解唯一,且泛化性能更好
模型

策略
我们希望找到具有“最大间隔”的划分超平面。
最后得到优化问题

算法
想要求解上述式子,得到最优解,以确定这个划分超平面所对应的模型
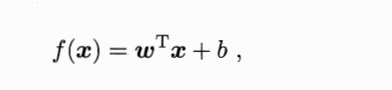
求解:
对于式子6.6的求解,这个优化问题为含不等式约束的优化问题,且是凸优化问题。
这里采用的是拉格朗日乘子法得到“对偶问题”
解“对偶问题”得出α
解出α后,求出w和b从而确定模型
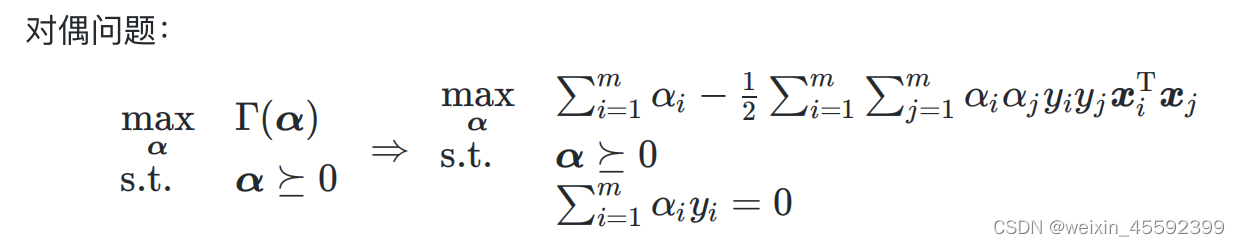
软间隔与正则化
前面的支持向量机有个前提:数据集是线性可分的。
,即存在一个超平面能将不同类的样本完全划分开。
为了缓解这个问题。想的一个办法就是允许支持向量机在一些样本上出错。因此,引入了“软间隔”的概念
软间隔
硬间隔:前面的支持向量机要求所有样本都必须满足式子6.3,
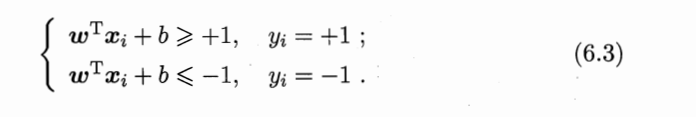
即所有样本都划分正确。
软间隔:
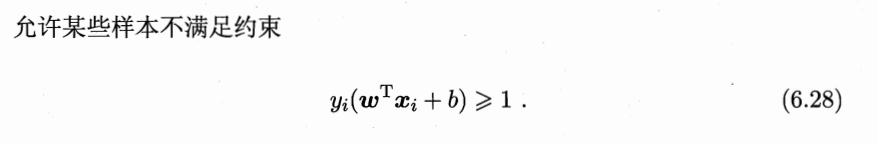

优化目标(策略)


这就是“软间隔支持向量机”
支持向量回归(SVR)
回归问题
SVR与传统回归模型计算损失的方式不同

策略
SVR优化问题可以写为

邱恩杰
采用拉格朗日乘子法得SVR的对偶问题,之后求解。
最后可得训练后模型: