[人工智能]基于（线性 | 逻辑）回归的思想分类（神经网络的由来）

基于回归的思想分类：

• 训练时：类 A 记为 1 ；类 B 记为 -1。
• 测试时：将接近 1 的数分为 A 类，接近 -1 的数分为 B 类。
  

1 线性回归

step 1

• 用贝叶斯决策计算每个样本的P(C₁|x)（后验概率）；P（C_i）称为先验概率，即不对样本进行任何观察的概率； P（X|C_i）称为概率密度，即x在C_i中的分布概率。Σ （P（C_i） P（X|C_i））称为全概率公式，即在所有情况下x发生的概率。
  

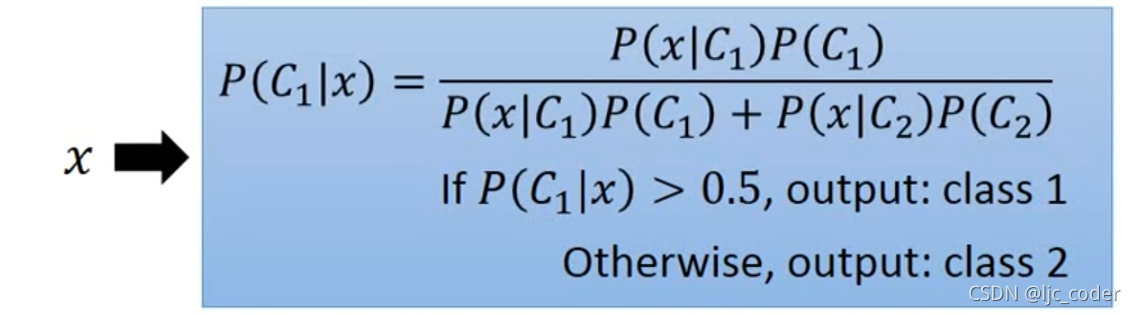
step2

• 通过高斯函数（可用其他方法，但都是为了找到最大化最大似然的参数），基于均值μ和协方差Σ得到一个最大化的最大似然值。
• 注：最大似然 即在已知试验结果（即是样本）的情况下，用来估计满足这些样本分布的参数，把可能性最大的那个参数作为真实的参数估计。
  
  

2 逻辑回归

step1

• 由不同的 w 和 b 得到函数 f 来表示样本 x 为 C_i 类的概率。
• **注：**σ为激活函数。
  
  

step2

• 将需要最小化的损失函数表示为Σ_n减去两个伯努利分布（p，q）的交叉熵。
• 注：交叉熵一般用于目标与预测值之间的差距，熵越小，差距越小。
  

3 对比&总结

Tip1

• 在第一阶段，线性回归的目标函数最终实际可以写为下图f_w,b的形式，由于线性回归的函数未加σ激活函数，因此其输出的是任意值；而逻辑回归则由于加了σ激活函数，输出值被限定在0，1之间。
• 而在第二阶段，线性回归的损失函数直接通过对期望值f_（x）和目标值yⁿ帽做平方差即可；而逻辑回归则要求对期望值f_（x）和目标值yⁿ帽求熵。
• 同时，两者的目标值yⁿ帽也不同，逻辑回归的目标值只有0，1来代表两类；而线性回归的目标值则不唯一。
  

Tip2

• 交叉熵和平方差的区别在于当初值里目标值（谷底）远时，交叉熵可以很快的接近目标值，而平方差则由于过于平坦，计算的会很慢。
  

Tip3

-下面对激活函数σ进行讲解，如下图，σ用于将最终的输出结果转化为0-1之间。

4 回归分类的局限性&神经网络的由来

• 由于逻辑回归的界限为一条直线。如遇下图的情况，红点和蓝点的分类无法表示出来。
  

• 可以通过特征转化让他们的位置改变来完成分类。
  

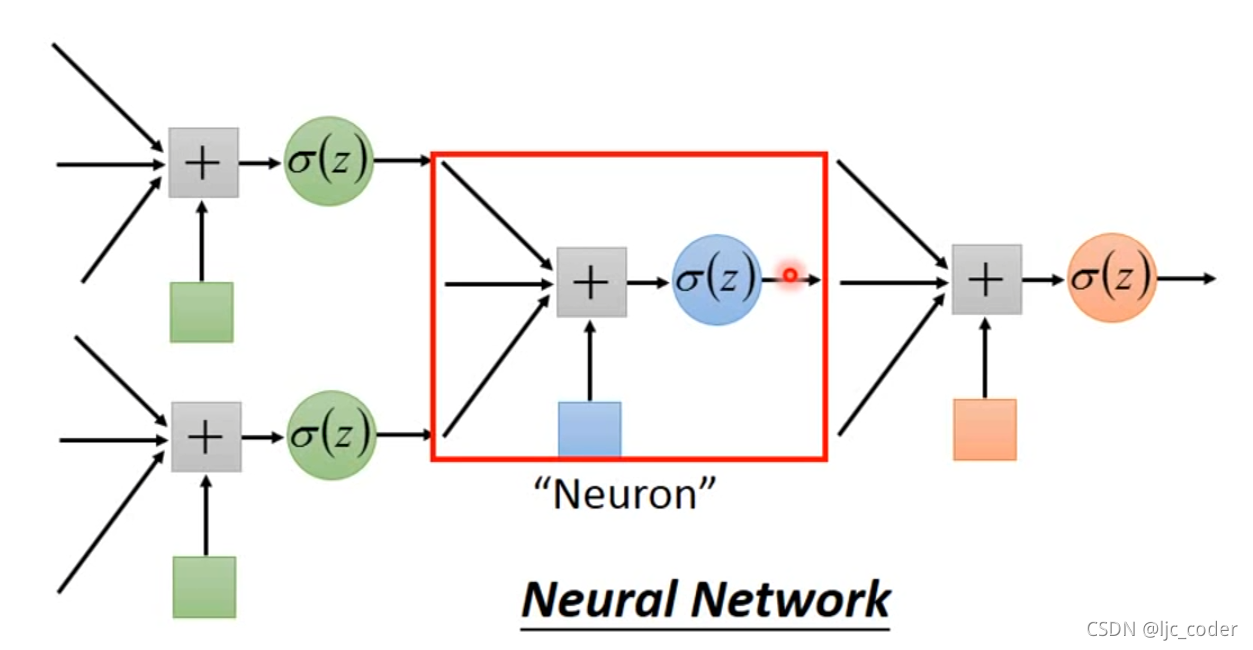
• 因此可以通过几个逻辑回归函数叠加来完成更加复杂的分类，如下图，而这种叠加的方式称为神经网络。