When Color Constancy Goes Wrong:
Correcting Improperly White-Balanced Images
阅读札记

??论文发表于2019年的CVPR。

Abstract

??本文方法主要解决校正白平衡不当的图像问题。校正白平衡不当问题真正难点不在于确定正确的白平衡是什么，而在于以下事实：相机内白平衡过程之后是几个相机特定的非线性颜色处理，这使得在后处理中校正图像的颜色具有挑战性。本文方法基于超过65,000张不正确白平衡图像及其相应的正确白平衡图像的数据集，引入k-近邻策略，实现计算非线性颜色映射函数来校正图像的颜色。

Introduction

??当白平衡（WB）不正确时会导致图像偏蓝/偏红，这对图片的观赏性以及对视觉算法的性能都存在不利影响。拍照时人们希望图像能正确地进行白平衡。前人工作主要在于确定正确WB是什么，然而该解决方案并不有效，并且没有在相机内处理管道的完整上下文中考虑WB。
??从传感器raw-RGB到sRGB的相机内颜色处理的简单模型可以表示为：
在这里插入图片描述
?? $I_{sRGB}$ ：3×N矩阵，包含sRGB空间中的图像值
?? $I_{raw}$ ：3×N矩阵，包含raw-RGB空间中的图像值
?? $N$ ：总像素数
?? $D$ ：3×3的WB对角矩阵
?? $T$ ：3×3 线性变换，它从白平衡raw-RGB映射到与设备无关的色彩空间，例如CIE-XYZ
?? $f (?)$ ：非线性函数，它复合了各种操作，包括颜色增强、色调处理和最终的sRGB伽马编码。（相机型号或相机设置不同， $f (?)$ 不同。）

??从等式可以看出，由于WB在处理链的早期应用，因此尝试使用对角矩阵对其进行校正是行不通的。

Method

算法框架图

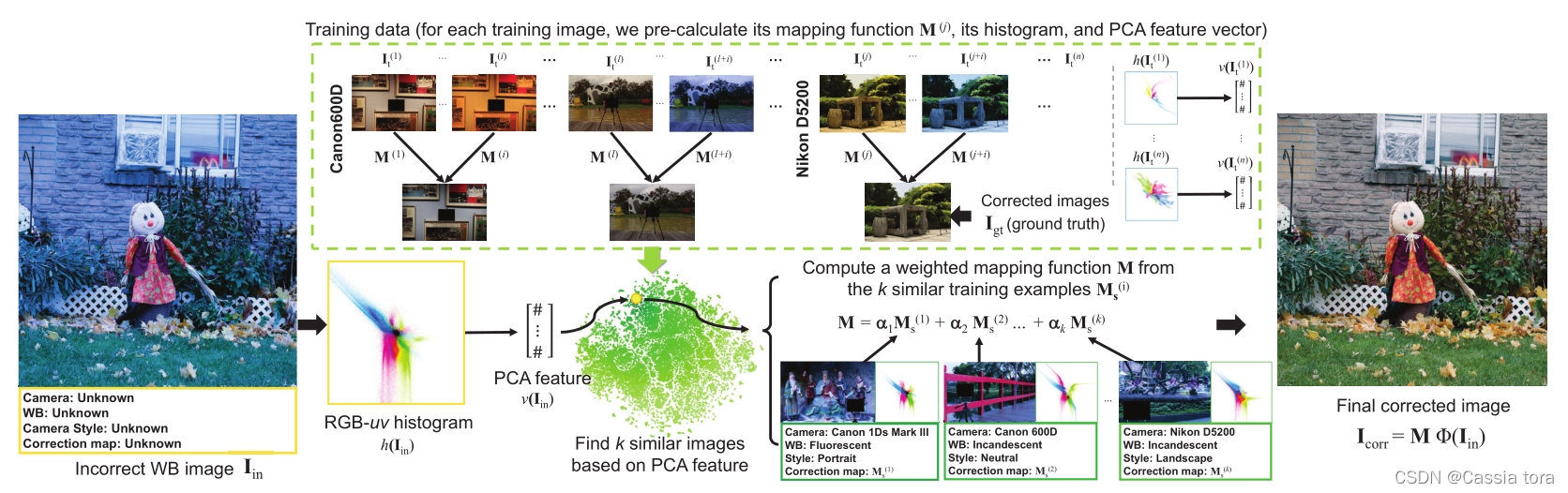
在这里插入图片描述

1、数据集生成

??本文的训练图像是从两个共开可用的照度估计数据集生成：NUS数据集和Gehler数据集，从这些数据集中生成了62,535张图像。
?? $?$ 使用不同WB预设来将raw-RGB图像渲染为sRGB图像。单个raw-RGB图像可以渲染为超过25个sRGB图像。这些图像构成了训练图像 ${I_t^{(1) },…,I_t^{(n) }\}$ 。
?? $?$ 手动从颜色再现图的中灰度块中选择“ground truth”白色，然后应用与相机相关的渲染生成正确的目标图像 $I_{gt}$ 。

2、颜色校正变换

??通过最小化以下等式来计算颜色校正矩阵 $M^{(i)}$ ，它将 $I_t^{(i)}$ 映射到 $I_{gt}^{(i)}$ ：
在这里插入图片描述
?? $I_t^{(i)}$ ：3×N矩阵，WB不正确的图像
?? $I_{gt}^{(i)}$ ：3×N矩阵，WB正确的参照图像
?? $_F$ ：F范数
?? $Φ$ ： $R,G,B]^T→[R,G,B,RG,RB,GB,R^2,G^2,B^2,RGB,1]^T$ ，将sRGB三元组投射到高维空间的内核函数。
?? $M^{(i)}$ ：3×11矩阵。

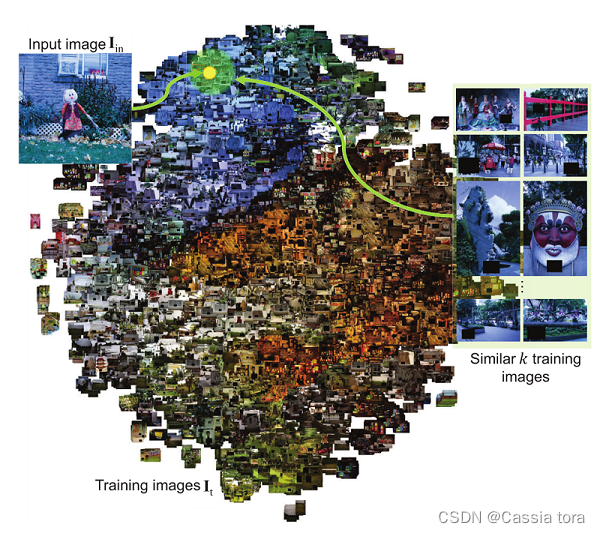
3、图像搜索

??颜色校正矩阵与图像的颜色分布有关，因此寻找相似图像的标准是基于颜色分布的。受前人工作启发，本文从对数色度空间构建了一个RGB-uv直方图，该直方图由以下等式描述的函数 $h (I)$ 生成：
在这里插入图片描述
?? $i$ ： $i=\{1,…,N\}$
?? $C$ ： $C∈\{1,2,3\}$ ，代表直方图中的每个颜色通道
?? $ε$ ：直方图bin的宽度。
???在归一化后取平方根会增加投影直方图特征的判别能力。
??用降维来提取表示每个RGB-uv直方图的紧凑特征。线性变换足以将向量化直方图 $vec(h(I))∈R^{(m×m×3)}$ 映射到新的低维空间。主成分分析 (PCA) 特征向量计算如下：
在这里插入图片描述
?? $v (I)$ ： $v(I)∈R^c$ 是包含c个主成分(PC)系数的PCA特征向量
?? $W$ ： $W=[w_1,w_2,…,w_c]$ , $w∈R^{(m×m×3)}$ 是奇异值分解计算出的PC系数矩阵
?? $b$ ： $b∈R^{(m×m×3)}$ ，是均值直方图向量。

???每个训练图像 $I_t^{(i)}$ 可以由少量PC系数 $v(I_t^{(i)})$ 。输入图像最终由 $v(I_{in})$ 表示。下图是基于相应PCA特征向量的训练图像可视化。
在这里插入图片描述

4、最终颜色校正

??给定一个输入图像，计算其PCA特征，并根据k-近邻策略在训练集中搜索具有相似特征的图像，得到k个相似图像对应的颜色校正矩阵M_s，最终校正矩阵M为M_s的加权线性组合，如下所示：
在这里插入图片描述
?? $α$ ：为径向基函数的加权向量：

?? $σ$ ：径向衰减因子
?? $d$ ：一个向量，包含给定输入特征和相似的k个训练特征之间的L2距离
??最后，校正后的图像 $I_{corr}$ 由以下等式产生：

Experiment

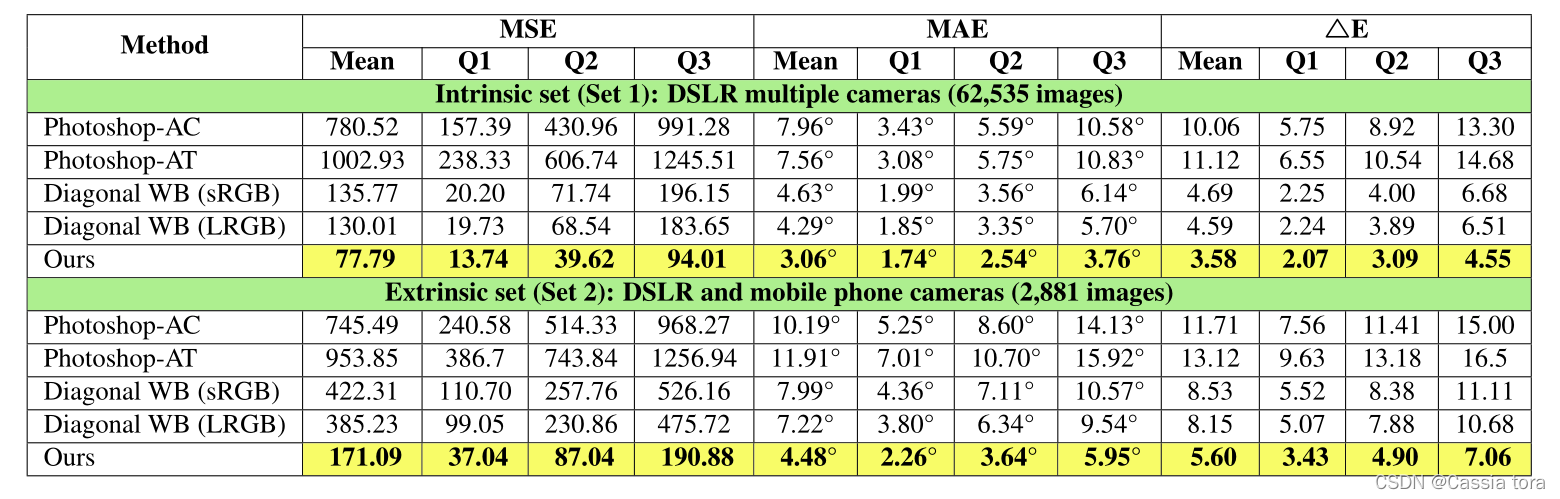
1、定量结果

评估方法：
????（i）均方误差(MSE)
????（ii）平均角度误差(MAE)
????（iii）?E
在这里插入图片描述

2、定性结果

在这里插入图片描述

Conclusion

??校正由具有错误WB设置的相机渲染的sRGB图像具有挑战性，本文提出了一种数据驱动的方法来纠正不正确的白平衡图像。，通过大量实验表明本文方法校正效果显著，且只需要少于24 MB的内存空间和少于1.5秒的时间即可校正全分辨率图像。此外，本文方法可以很好地推广到不包含在我们训练集中的图像。但本文方法在某些类型的输入上确实失败了，这些通常是具有大量饱和色彩的强烈偏色的图像，如图所示：
在这里插入图片描述