[人工智能]深度学习基础

深度学习基础

本系列为跟着李沐学习深度学习系列整理的笔记，在此自己总结梳理一遍，加深理解和记忆。更详细的视频教程可参考动手学深度学习 PyTorch版，笔记教程可参考动手学习深度学习

系列文章目录

• 深度学习预备知识

前言

本篇主要介绍了深度学习的基础知识，包括线性回归、softmax回归、多层感知机等。

一、线性回归

1.线性回归基本要素

模型定义

对于特征集合 X ，预测值$\hat{\mathbf{y}}\in {\mathbb{R}}^n$ 可以通过矩阵-向量乘法表示为：
$$\hat{\mathbf{y}}=\mathbf{X}\mathbf{w}+b$$

损失函数

当样本 i 的预测值为${\hat{y}}^{(i)}$，应的真实标签为$y^{(i)}$时，平方误差可以定义为以下公式：
$$l^{(i)}(\mathbf{w},b)=\frac{1}{2}{\left({\hat{y}}^{(i)}?y^{(i)}\right)}^2$$
整个样本上的损失为：
$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n{l}^{(i)}(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{?}{\mathbf{x}}^{(i)}+b?y^{(i)}\right)}^2.$$
在模型训练中，我们希望找出一组模型参数来使训练样本平均损失最小：
$$w^{?},b^{?}=\underset{w_{,}b}{\mathrm{argmin}}?\left(w,b\right)$$

优化算法

在无法用公式表达出来求最小化误差问题时，采用有限次迭代的方式尽可能降低损失函数的值（数值解），一般采用小批量随机梯度下降法。
$$(\mathbf{w},b)\leftarrow (\mathbf{w},b)?\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{?}_{(\mathbf{w},b)}{l}^{(i)}(\mathbf{w},b)$$

2.线性回归从零开始实现

%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random

#生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs,
                       dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                       dtype=torch.float32)


# 读取数据
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  # 样本的读取顺序是随机的
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # 最后一次可能不足一个batch
        yield  features.index_select(0, j), labels.index_select(0, j)


# 初始化参数模型        
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True) 


# 定义模型   
def linreg(X, w, b):  
    return torch.mm(X, w) + b


# 定义损失函数  
def squared_loss(y_hat, y):  
    # 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
    return (y_hat - y.view(y_hat.size())) ** 2 / 2
  
# 定义优化算法 
def sgd(params, lr, batch_size): 
    for param in params:
        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data

        
# 训练模型
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
batch_size = 10

for epoch in range(num_epochs):  # 训练模型一共需要num_epochs个迭代周期
    # 在每一个迭代周期中，会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）。X
    # 和y分别是小批量样本的特征和标签
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()  # l是有关小批量X和y的损失
        l.backward()  # 小批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数

        # 不要忘了梯度清零
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

3.线性回归简介实现

import numpy as np
import torch
import torch.utils.data as Data
from d2l import torch as d2l
from torch import nn 

#生成数据集
num_inputs = 2
num_examples = 1000
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features = torch.randn(num_examples, num_inputs,
                       dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b

labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                       dtype=torch.float32)

# 读取数据
batch_size = 10
dataset =  Data.TensorDataset(features,labels) # 将训练数据的特征和标签组合
data_iter = Data.DataLoader(dataset,batch_size,shuffle=True) # 随机读取小批量

# 定义模型   
net = nn.Sequential(nn.Linear(2,1))


# 初始化参数模型    
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)


# 定义损失函数  
loss = nn.MSELoss()
  
# 定义优化算法 
train = torch.optim.SGD(net.parameters(),lr=0.03)

        
#训练模型
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y.view(-1, 1))
        train.zero_grad()
        l.backward()
        train.step()
    l = loss(net(features),labels.view(-1, 1))
    print(f'epoch {epoch + 1}, loss {l:f}')
    
w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

二、softmax回归

1.softmax回归模型

softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax回归的输出值个数等于标签里的类别数。softmax回归的矢量计算表达式为
$$\begin{array}{rl}& \mathbf{O}=\mathbf{X}\mathbf{W}+\mathbf{b}\\ & \hat{\mathbf{Y}}=\mathrm{softmax}(\mathbf{O})\\ & {\hat{y}}_j=\frac{\exp \left(o_j\right)}{{\sum }_k\exp \left(o_k\right)}\end{array}$$

交叉熵损失函数

我们可以像线性回归那样使用平方损失函数，然而，想要预测分类结果正确，我们其实并不需要预测概率完全等于标签概率。所以使用交叉熵（cross entropy）作为衡量两个概率分布差异的测量函数。
$$H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)=?\sum _{j=1}^q{y}_j^{(i)}\log {\hat{y}}_j^{(i)}=?\log {\hat{y}}_y^{(i)}(i)$$
其中带下标的$y_j^{(i)}$是向量$y^{(i)}$中非0即1的元素,，我们知道向量$y^{(i)}$ 中只有第i个元素为1，其余全为0。也就是说，交叉熵只关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果正确。当然，遇到一个样本有多个标签时，例如图像里含有不止一个物体时，我们并不能做这一步简化。
假设训练数据集的样本数为nn，交叉熵损失函数定义为
$$?(\mathbf{\Theta })=\frac{1}{n}\sum _{i=1}^{n}H\left({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}\right)$$
其中$\mathbf{\Theta }$代表模型参数。最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。

2.softmax回归的从零开始实现

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
#初始化参数
num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

#定义softmax操作
def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

#定义模型
def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

#定义损失函数
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

#定义优化函数
lr = 0.1
def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

#定义分类的准确率
def accuracy(y_hat, y):  #@save
    """计算预测正确的数量。"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # Accumulator为自己写的一个累加的类。正确预测数、预测总数
    for X, y in data_iter:
        metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]
    
#训练
def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）。"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.backward()
            updater.step()
            metric.add(float(l) * len(y), accuracy(y_hat, y),
                       y.size().numel())
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
            metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练准确率
    return metric[0] / metric[2], metric[1] / metric[2]

        
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc']) #一个绘图函数
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc
    

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)


#预测
def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

训练结果如下：

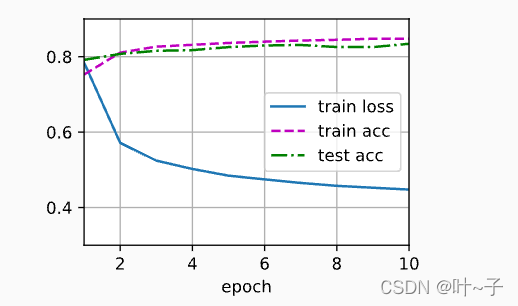
预测结果如下：

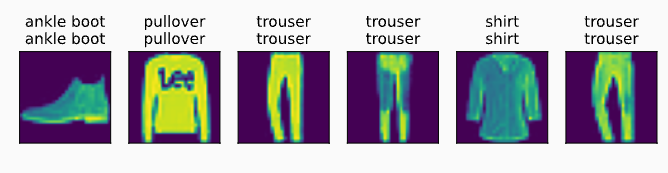
3.softmax简洁实现

#获取数据集
import torch
from d2l import torch as d2l
from torch import nn   #nn是神经网络的缩写



batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#定义和初始化模型
net = nn.Sequential(nn.Flatten(),nn.Linear(784,10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight,std=0.01)
        
net.apply(init_weights);

#定义损失函数
loss = nn.CrossEntropyLoss()

#定义优化算法
trainer = torch.optim.SGD(net.parameters(),lr=0.1)


#训练
def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）。"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.backward()
            updater.step()
            metric.add(float(l) * len(y), accuracy(y_hat, y),
                       y.size().numel())
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
            metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练准确率
    return metric[0] / metric[2], metric[1] / metric[2]

        
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc']) #一个绘图函数
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

num_epochs = 10
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)

三、多层感知机

1.多层感知机

多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号，多层感知机按以下方式计算输出：
$$\begin{array}{rl}\mathbf{H}& =?\left(\mathbf{X}{\mathbf{W}}_h+{\mathbf{b}}_h\right)\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}_o+{\mathbf{b}}_o\end{array}$$
其中$?$表示激活函数。在分类问题中，我们可以对输出$\mathbf{O}$做softmax运算，并使用softmax回归中的交叉熵损失函数。 在回归问题中，我们将输出层的输出个数设为1，并将输出$\mathbf{O}$直接提供给线性回归中使用的平方损失函数。

2.多层感知机从零开始实现

#从零开始实现
import torch
from torch import nn
from d2l import torch as d2l


batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#初始化模型参数
num_inputs,num_outputs,num_hiddens = 784,10,256

W1 = nn.Parameter(torch.randn(num_inputs,num_hiddens,requires_grad=True)*0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens,requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens,num_outputs,requires_grad=True)*0.01)
b2 = nn.Parameter(torch.zeros(num_outputs,requires_grad=True))

params = [W1,b1,W2,b2]

#激活函数
def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X,a)

#模型
def net(X):
    X = X.reshape((-1,num_inputs))
    H = relu(X @ W1 + b1)
    return (H @ W2 + b2)

#损失函数
loss = nn.CrossEntropyLoss()

#训练
num_epochs,lr = 10,0.1
updater = torch.optim.SGD(params,lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,updater)

3.多层感知机简洁实现

#简洁实现

net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Linear(256,10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)