[人工智能]学习笔记5--摄像头标定之内参标定

本系列博客包括6个专栏，分别为：《自动驾驶技术概览》、《自动驾驶汽车平台技术基础》、《自动驾驶汽车定位技术》、《自动驾驶汽车环境感知》、《自动驾驶汽车决策与控制》、《自动驾驶系统设计及应用》，笔者不是自动驾驶领域的专家，只是一个在探索自动驾驶路上的小白，此系列丛书尚未阅读完，也是边阅读边总结边思考，欢迎各位小伙伴，各位大牛们在评论区给出建议，帮笔者这个小白挑出错误，谢谢！
此专栏是关于《自动驾驶汽车环境感知》书籍的笔记。

1.摄像头标定之内参标定

1.1 概述

1. 标定传感器是自动驾驶感知系统中的必要环节，是后续传感器融合的必要步骤和先决条件，目的是将两个或多个传感器变换到统一的时空坐标系，使得传感器融合具有意义，是感知决策的关键前提；
2. 车载摄像头以一定的角度和位置安装在车辆上，为了将车载摄像头采集到的环境数据与车辆行驶环境中的真实物体相对应，即找到车载摄像头所生成的图像像素坐标系中的点坐标与摄像机环境坐标系中的点坐标之间的转换关系，需要进行摄像头标定；
3. 传感器的标定是建立传感器输出与现实中的值的对应关系；
4. 单目视觉的标定实质是建立物体在环境坐标系中的坐标与图像坐标系中的坐标之间的关系；

1.2 摄像头内参数标定

1.2.1 摄像头模型的建立

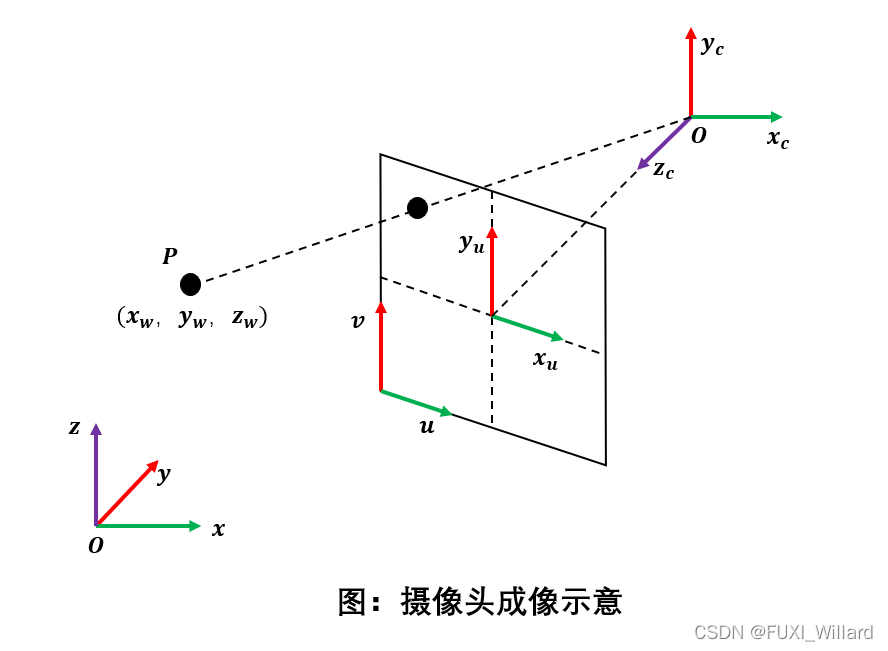
上图说明：坐标系$Oxyz$是环境坐标系；设现实世界中一个物体P，在环境坐标系中的位置为$(x_w，y_w，z_w)$；为了得到P在图像上的投影位置，需要建立三个辅助坐标系：摄像头坐标系、图像物理坐标系、图像像素坐标系，最终需要得到的是P点在图像像素坐标系上的投影；

1. 摄像头坐标系与环境坐标系的转换
   

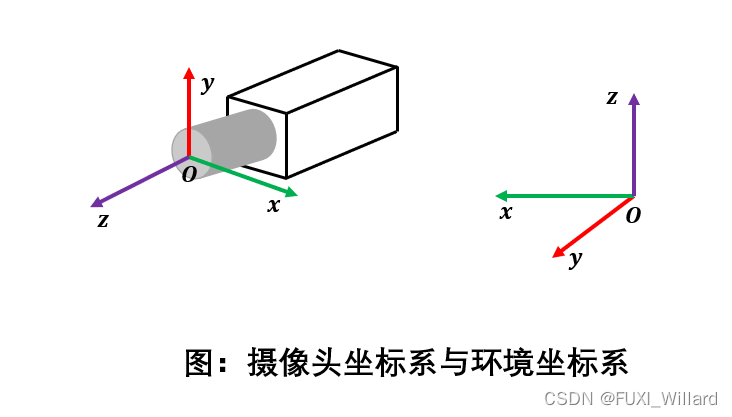
   1. 上图说明：摄像头坐标系以镜头中心为原点，以垂直镜头平面的直线为z轴建立空间直角坐标系，x轴与y轴在镜头平面上，x，y，z满足右手坐标系；
   2. 摄像头在空间中有一个位置，可以建立环境坐标系与摄像头坐标系之间的关系[R，T]，其中T为摄像头坐标系原点相对于环境坐标系原点的平移，即摄像头的镜头中心在环境坐标系的坐标，R为摄像头坐标系相对环境坐标系的选择矩阵；
   3. 空间中的点P在摄像头坐标系中的坐标可以通过以下公式求解：$$?\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}?=R?\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}?+T$$
      对上述公式进行转换，可得：
      $$?\begin{array}{c}{x}_c\\ y_c\\ z_c\\ 1\end{array}?=\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]?\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}?$$

2. 图像坐标系与图像像素坐标系
   

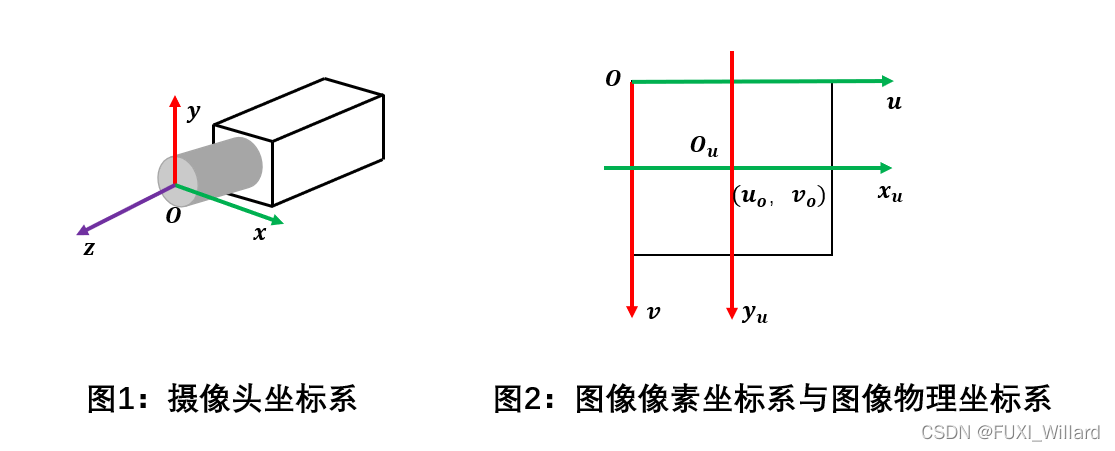
   1. 上图说明：计算机视觉中，图像常以点阵的方式存储，每个像素对应着点阵中的一行与一列；图像像素坐标系完全对应这种关系；图像像素坐标系以图像左上角为原点，向右的方向为u坐标轴，向下的方向为v轴，像素在该坐标系下用二元组(u,v)表示；
   2. 图像像素坐标系符合计算机图像处理逻辑，但图像像素坐标系坐标(u,v)仅仅代表像素的列数与行数，不带有任何物理单位，空间中的坐标点则必须用带有单位(如厘米、米等)的量来表示，因此引入图像物体坐标系；定义摄像头光轴与图像平面的交点为图像主点，图像物理坐标系以主点为原点，x轴与y轴分别平行于图像像素坐标系的u轴与v轴；
   3. 设像元底边长为width，高为height，主点在图像像素坐标系下的坐标为$(u_o,v_o)$，在不考虑图像畸变的情况下，图像物理坐标系下的点$(x_l，y_l)$在图像像素坐标系下的坐标通过如下公式解算： $$?\begin{array}{c}u\\ v\\ 1\end{array}?=?\begin{array}{ccc}\frac{1}{width}& 0& u_o\\ 0& \frac{1}{height}& v_o\\ 0& 0& 1\end{array}??\begin{array}{c}{x}_l\\ y_l\\ 1\end{array}?$$

3. 小孔成像与图像物理坐标系
   

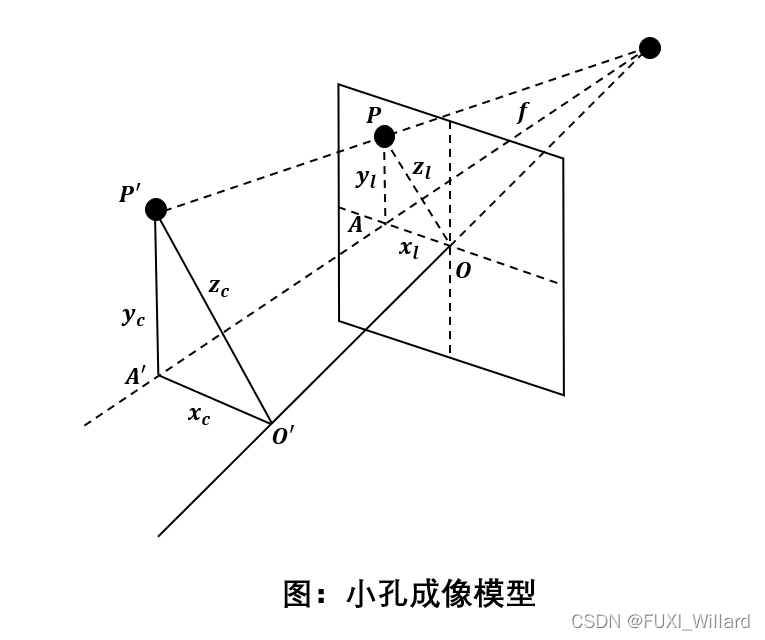
   1. 摄像头成像的理论基础是小孔成像；
   2. 图像物理坐标系的原点与摄像机的光学中心重合；
   3. 当摄像头坐标系的x轴与y轴与图像物理坐标系的x轴与y轴平行时，可以构建起图像坐标系与摄像机坐标系之间的关系；
   4. 对于物体P，在摄像机坐标系下的坐标为$(x_c,y_c,z_c)$；根据几何关系，有：$$\Delta OPA～\Delta O^{\prime }{P}^{\prime }{A}^{\prime }$$
      因此，有如下关系：$$\frac{x_l}{x_c}=\frac{y_l}{y_c}=\frac{f}{z_c}$$
      则有：$$x_l=\frac{1}{z_c}?f?x_c，y_l=\frac{1}{z_c}?f?y_c$$
      令$s=z_c$，则有：$$s??\begin{array}{c}{x}_l\\ y_l\\ 1\end{array}?=?\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}??\begin{array}{c}{x}_c\\ y_c\\ z_c\\ 1\end{array}?$$

4. 环境坐标系与图像像素坐标系的转换
   得到环境坐标系-摄像机坐标系、摄像机坐标系-图像像素坐标系之间的关系后，可解算环境坐标系与图像像素坐标系之间的转换关系；对现实世界的点P，其在环境坐标系下的坐标为$(x_w,y_w,z_w)$，在图像中的位置为$(u,v)$，则有如下关系：$$s??\begin{array}{c}u\\ v\\ 1\end{array}?=?\begin{array}{cccc}\frac{1}{width}& 0& u_o& \\ 0& \frac{1}{height}& v_o& \\ 0& 0& 1& \end{array}???\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}??\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]??\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}?$$
   化简：$$s??\begin{array}{c}u\\ v\\ 1\end{array}?=?\begin{array}{cccc}{\alpha }_x& 0& u_o& 0\\ 0& {\alpha }_y& v_o& 0\\ 0& 0& 1& 0\end{array}?\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]?\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}?=M_1{M}_2{X}_w$$
   其中，${\alpha }_x=\frac{f}{width}，{\alpha }_y=\frac{f}{height}$；
   1. 矩阵$M_2$为环境坐标系到摄像头坐标系的坐标转换关系，是摄像头在世界坐标系下的位置姿态矩阵；
   2. 在计算机视觉中，确定$M_2$矩阵的过程称为视觉定位；
   3. 自动驾驶汽车需要定期对摄像头位置进行重新标定，这一过程称为校准；
   4. 矩阵$M_1$，其四个常量${\alpha }_x，{\alpha }_y，u_o，v_o$与摄像机的焦距、主点、传感器等设计技术指标有关，而与外部因素(如周边环境、摄像机位置)无关，称为摄像头内参；
   5. 内参在摄像头出厂时确定，往往通过实验方式确定摄像头内参，对于单目摄像头的标定，指通过实验手段确定摄像头的内参；

1.2.2 摄像头畸变矫正

1. 摄像头通常存在透镜畸变，即物点在实际的摄像头成像平面上生成的像与理想成像之间存在一定光学畸变误差，畸变误差主要分为径向畸变误差和切向畸变误差；
2. 径向畸变误差：沿着透镜半径方向分布的畸变，产生的原因是光线在远离透镜中心的地方比靠近中心的地方更加弯曲；
3. 切向畸变误差：由于透镜本身与摄像头传感器平面(成像平面)或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致；
4. 畸变是透镜的固有特性，无法消除，只能改善；
5. 在自动驾驶汽车上，影响摄像头工作的畸变一般两种：桶形畸变和枕形畸变；
6. 枕形畸变：由镜头引起的画面向中间"收缩"的现象；在使用长焦镜头或变焦镜头的长焦端时，容易看到枕形畸变；
7. 桶形畸变：由于镜头中透镜物理性能及镜片组结构引起的成像画面呈桶形膨胀状的失真现象；在使用广角镜头或使用变焦镜头的广角端时，容易看到桶形畸变；桶形畸变与枕形畸变统称径向畸变；
8. 对一般摄像头来讲，图像的径向畸变描述为低阶多项式模型；设观测到的图像中的某个像素$(u，v)$在没有畸变情况下的图像像素坐标为$(u^{\prime }，v^{\prime })$，则两者之间的变换通过以下公式确定：$$\{\begin{array}{cc}u& =u^{\prime }(1+k_1{r}_c^2+k_2{r}_c^4)\\ v& =v^{\prime }(1+k_3{r}_c^2+k_4{r}_c^4)\end{array}$$
   其中：$r_c^2=u^{\prime 2}+v^{\prime 2}；k_1，k_2，k_3，k_4$称为径向畸变系数，属于摄像头内参；
9. 标定畸变系数方法：铅垂线方法(plumb-line method)；基本思想：拍摄多条直线，特别是与图像的边缘对齐的场景图像，然后通过调整畸变参数来使得图像中所有的线条都变成直线；
10. 标定畸变系数其他方法：使用若干重叠图像，将径向畸变参数的估计与图像配准过程相结合，典型代表：Sawhney and Kumar(2009)，其将多层次运动模型与二次畸变矫正项用在一个从粗到精的过程中，使用基于亮度的最小化方法计算配准；Stein(1997)使用基于特征的方法，结合三维运动模型和二次径向畸变，进行畸变矫正与配准；

1.2.3 摄像头内参标定方法

1. 常用标定方法：平面标定模式与自标定；
2. 平面标定模式：指制作一块标定板，在工作区的空间内使用一种可控的移动方式来移动该目标，这种方法称为"N-平面标定法"；
3. 平面标定模式应用最广泛的是：张正友标定法；张正友标定法通过在不同位置拍摄棋盘标定板的方式，在每个图像中找到棋盘标定板的内角点，通过内角点之间的对应关系建立对矩阵$B=K^{?T}{K}^{?1}$的约束，从而恢复内参矩阵$K$；
4. 当没有标定板时，可以通过摄像机的运动来进行标定，这种不使用已知目标进行标定的方法称为自标定；