基本信息
论文:https://arxiv.org/pdf/2006.12030.pdf
代码:https://github.com/yangyanli/DO-Conv
核心逻辑

上图是卷积核在一个滑动窗口区域上的一次标准卷积操作,注意这里没有滑动的过程,就是一次卷积操作。
其中M和N是卷积核在两个spatial方向上的大小,比如我们一般使用3*3卷积核,那这里就是M=3和N=3,这个图片就是指我们在Cin * 3 * 3的原图P上做了一次卷积操作,得到了1 * Cout的结果。(不过图中显示的是M * N =4,一样的道理)
另两个维度Cin和Cout是输入的维度数和输出的维度数
图中的W是weight的缩写,指卷积核的权重张量;P是patch的缩写,指一次滑动窗口的那一小片区域;O是Output的缩写,指本次卷积操作的输出
如果把W看成两层图的话
把W的第一层跟P对应位置相乘并相加得到O向量的第一个数
把W的第二层跟P对应位置相乘并相加得到O向量的第二个数

上图是卷积核在一个滑动窗口区域上的一次深度卷积操作,不了解深度卷积的可以去搜索一下。参数跟上边一样,不同的是,这次的卷积操作是:
依然把W看做两层
第一层的黄色区域有M * N 个值,跟P的黄色区域的M * N 个值相乘并相加,得到O的黄色区域的一个值
第二层的黄色区域有M * N 个值,跟P的黄色区域的M * N 个值相乘并相加,得到O的黄色区域的另一个值
以此类推得到蓝色和绿色的各两个值
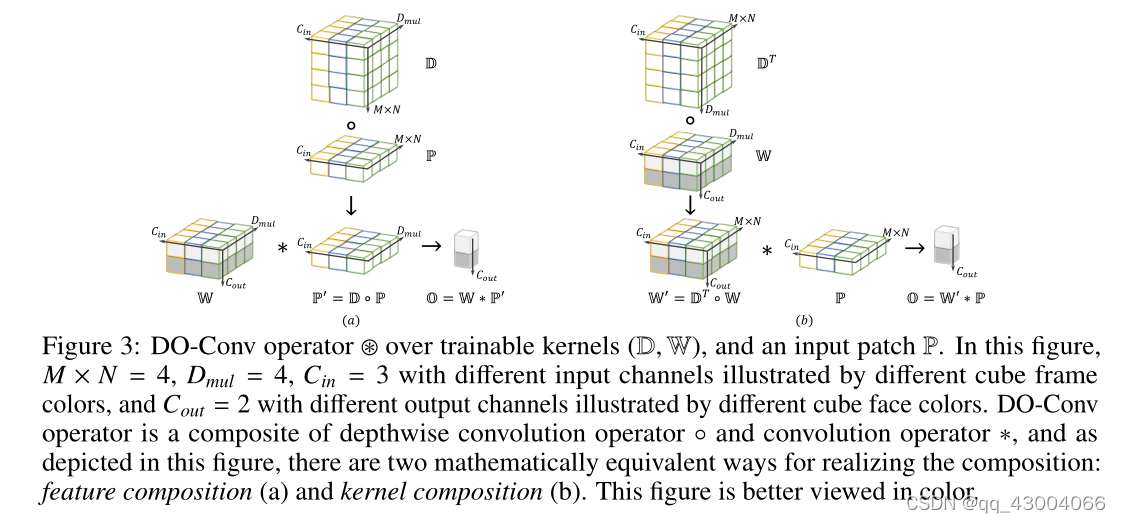
作者尝试把标准卷积操作和深度卷积结合到一起,上图是Do-Conv卷积的两种形式
图a是先进行一次深度卷积得到Cin和Dmul,然后紧接着进行标准卷积得到最终的O向量
图b则是把深度卷积核的参数和标准卷积核的参数直接乘到一起,然后再跟原图的输入进行一次标准卷积,也能得到相同的结果
不过这两种方式的计算量不一样

经过上图对比之后,最终还是选用了图b的方式
作者在训练的时候更新两个卷积核的参数,然后在推理的时候把这些参数先按照图b的形式变成一个标准卷积的参数保存下来,然后根据这个参数进行推理。理论上推理时的计算量跟标准卷积相同,并不会因为增加了一个深度卷积核就变慢
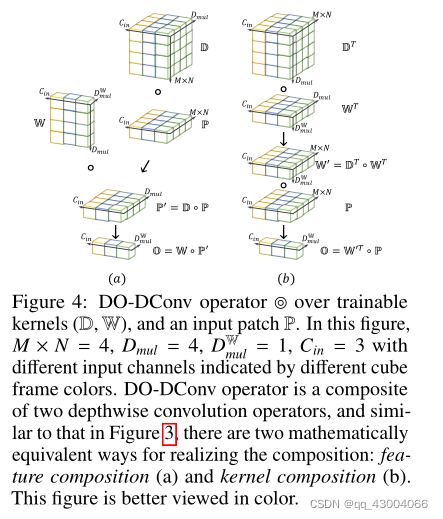
除了把标准卷积加一个深度卷积操作之外,深度卷积本身也可以加上一层深度卷积
图中的D表示额外加上的深度卷积核,W表示原本的深度卷积核
图a是先用额外的深度卷积核进行深度卷积之后,再经过一次原本的深度卷积
图b是把两个深度卷积核合并起来
这里同样是在训练的时候得到两个深度卷积核的参数,然后在推理的时候把它们合并起来,并不会增加推理时的计算开销
优势
因为训练时多了一次深度卷积,所以理论上可以加快训练,并收敛到更好的参数组合
之后的实验也证明了这一点,加入了一次深度卷积后,尽管推理时参数量没有变化,网络依然得到了更高的分类精度