1 损失函数

我们先用sklearn生成一个多标签分类数据集。

from sklearn.datasets import make_multilabel_classification

X, y = make_multilabel_classification(n_samples=1000,
                                          n_features=10,
                                          n_classes=3,
                                          n_labels=2,
                                          random_state=1)
print(X.shape, y.shape)

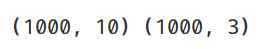
在这里插入图片描述
看一下标签长啥样。

每一行都是0、1标签，1可能有多个，这就是多标签了。
由于仍然是二分类（标签只有0和1），所以激活函数用Sigmoid（对输出的每一个维度用Sigmoid）。这个时候损失函数就是BCELoss。
如果是普通的二分类，Sigmoid的输出是一个值。用 $N$ 表示样本数量， $p_n$ 表示预测第 $n$ 个样本为正例的概率， $y_n$ 表示第 $n$ 个样本的标签，则BCELoss计算公式为：
$loss=-\frac{1}{N}\sum_{n=1}^{N}y_n×log(p_n)+(1-y_n)×log(1-p_n)$
那么对于多标签分类呢？BCELoss会计算每一个维度上的损失然后求平均。
举个例子，假如模型某个输出是[0.2，0.6，0.8]，真实值是[0，0，1]，那么该样本损失可以计算如下：
$a=0×ln(0.2)+1×ln(1-0.2)\\ b=0×ln(0.6)+1×ln(1-0.6)\\ c=1×ln(0.8)+0×ln(1-08)\\ loss=(a+b+c)/3$
这只是单个样本的损失，最后还需要求所有样本损失的平均值。但是你就不用管了，只需要知道多标签分类用Sigmoid+BCELoss就可以完成损失计算。还有一个函数叫BCEWithLogitsLoss，是Sigmoid和BCELoss的结合。如果损失函数用这个，Sigmoid就可以不用。

2 准确率计算

依然是上面的例子，模型的输出是[0.2，0.6，0.8]，真实值是[0，0，1]。准确率该怎么计算呢？

pred = torch.tensor([0.2, 0.6, 0.8])
y = torch.tensor([0, 0, 1])
accuracy = (pred.ge(0.5) == y).all().int().item()
accuracy
# output : 0

首先ge函数将pred中大于等于0.5的转化为True，小于0.5的转化成False，再比较pred和y（必须所有维度都相同才算分类准确），最后将逻辑值转化为整数输出即可。
训练时都是按照一个batch计算的，那就写一个循环吧。

pred = torch.tensor([[0.2, 0.5, 0.8], [0.4, 0.7, 0.1]])
y = torch.tensor([[0, 0, 1], [0, 1, 0]])
accuracy = sum(row.all().int().item() for row in (pred.ge(0.5) == y))
accuracy
# output : 1

3 完整代码

from sklearn.datasets import make_multilabel_classification
import torch
from torch.utils.data import DataLoader
from sklearn.model_selection import train_test_split

def get_dataset():
    X, y = make_multilabel_classification(n_samples=1000,
                                          n_features=10,
                                          n_classes=3,
                                          n_labels=2,
                                          random_state=1)
    return X,y

n_inputs, n_outputs = X.shape[1], y.shape[1]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.33,random_state=42)
X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
y_train = torch.from_numpy(y_train).float()
y_test = torch.from_numpy(y_test).float()

train_data=[(X,y) for X,y in zip(X_train,y_train)]
train_loader = DataLoader(train_data, batch_size=64,shuffle=True)

class MLP(nn.Module):
    def __init__(self, n_inputs, n_outputs, num_hiddens):
        super(MLP, self).__init__()
        self.linear_relu_stack = nn.Sequential(
            nn.Linear(n_inputs, num_hiddens),
            nn.ReLU(),
            nn.Linear(num_hiddens, n_outputs), 
            nn.Sigmoid())

    def forward(self, x):
        outputs = self.linear_relu_stack(x)
        return outputs


num_hiddens = 30
model = MLP(n_inputs, n_outputs, num_hiddens)
print(model)

loss = nn.BCELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

def train(train_loader, X_test, y_test, model, loss, num_epochs, batch_size,
          optimizer):
    batch_count = 0
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_loader:
            pred = model(X)
            l = loss(pred, y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            train_l_sum += l.item()
            train_acc_sum += sum(row.all().int().item()
                                 for row in (pred.ge(0.5) == y))
            n += y.shape[0]
            batch_count += 1
        test_acc = evaluate_accuracy(X_test, y_test, model)
        print(
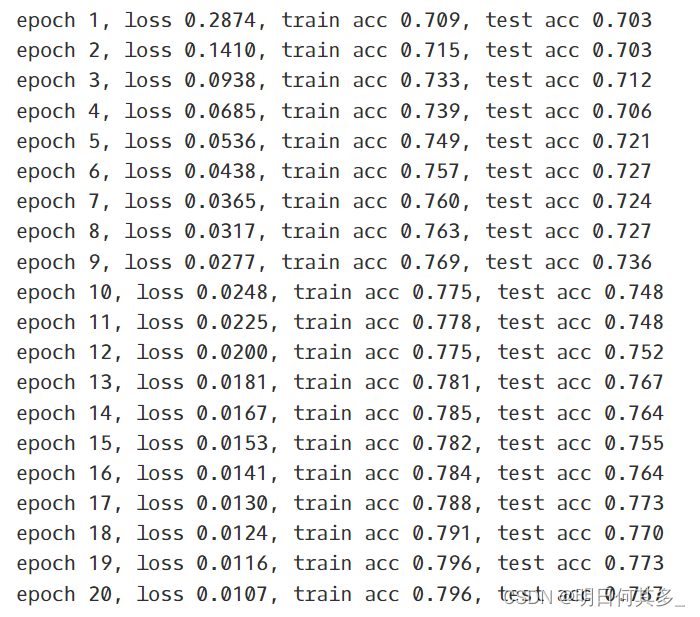
            'epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
            % (epoch + 1, train_l_sum / batch_count, train_acc_sum / n,
               test_acc))

num_epochs, batch_size = 20, 64
train(train_loader, X_test, y_test, model, loss, num_epochs, batch_size,optimizer)