[人工智能]用matplotlib.pyplot绘图

import matplotlib.pyplot as plt
import numpy as np

# x = [4 * np.pi * i / 100 for i in range(100)]
# y = [math.cos(i) for i in x]
x = np.arange(0, 4 * np.pi, 0.1)
y = np.cos(x)
plt.figure("tk")  # 命名绘图窗口
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, y)
plt.text(4, 1, "y=cos(x)")  # 在(4, 1)的位置添加注解
plt.show()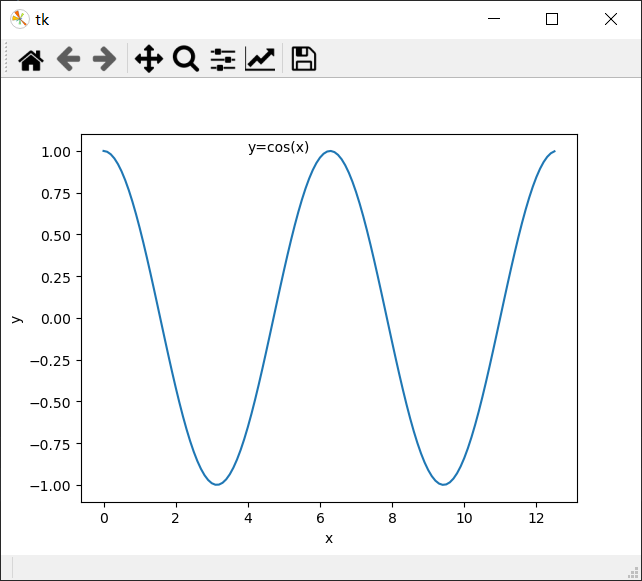

import numpy as np
import matplotlib.pyplot as plt


def f(t):
    return np.exp(-t) * np.sin(2 * np.pi * t)


t1 = np.arange(0.0, 5.0, 0.1)  # 返回一个有终点和起点的固定步长的排列
t2 = np.arange(0.0, 5.0, 0.02)
fig = plt.figure(1)  # 新建一个名叫Figure1的画图窗口
plt.subplot(211)  # 图像是2×1的,即最多2张图,当前绘制的子图为第一个(按行顺序数)
plt.plot(t1, f(t1), 'bo', t2, f(t2), 'k')  # b为blue,o为实心圆,k为black
plt.subplot(212)
plt.plot(t2, np.sin(2 * np.pi * t2), 'r--')  # r为red,--为破折线
plt.show()

随机生成满足mu为100 、sigma为20的正态分布的10万个智商数据，使用Matplotlib.pyplot的hist()函数绘制其直方图

import numpy as np
import matplotlib.pyplot as plt

# 随机生成满足mu为100、sigma为20的正态分布的10万个智商数据
mu, sigma = 100, 20
x = mu + sigma * np.random.randn(100000)
plt.hist(x, bins=50, density=1, facecolor='g', alpha=0.75)
'''
bins指定有几条柱状图，alpha设置透明度
参数normed已弃用，改为density，如果为True，则返回元组的第一个元素将是归一化的计数，以形成概率密度，即n/(len(x)`dbin)，
即直方图的积分总和为1。如果“stacked”也为True，直方图的总和将被归一化为1。
'''
plt.xlabel('IQ')
plt.ylabel('Probability')
plt.title('Histogram of IQ')
plt.axis([40, 180, 0, 0.03])  # 横纵坐标范围
plt.grid(True)  # 设置网格
plt.show()