时隔三个月终于有时间更新了…在ppt的夹缝中练习。
期待圣诞节!!!
卷积神经网络:Step by Step
欢迎来到第四课的第一个作业!在本任务中,您将在numpy中实现 卷积(CONV)和池化(POOL)层,包括前向传播和( 可选) 反向传播
【符号】:
- 上标
[
l
]
[l]
[l]表示第1层的对象。
- 示例: a [ 4 ] a^{[4]} a[4]表示第四层激活。 W [ 5 ] W^{[5]} W[5]和 b [ 5 ] b^{[5]} b[5]是第五层参数。
- 上标
(
i
)
(i)
(i)表示来自第
i
i
i个样本的对象。
- 示例: x ( i ) x^{(i)} x(i)是第 i i i个训练样本输入。
- 小写
i
i
i表示向量的第
i
i
i项。
- 示例: a i [ l ] a^{[l]}_i ai[l]?表示第 𝑙 𝑙 l层中第 i i i个激活值,假设这是一个全连接(FC)层。
- n H n_H nH?, n W n_W nW? 和 n C n_C nC?分别表示给定层的高度,宽度和通道数。如果你想特指某层 l l l,也可以写作 n H [ l ] n_H^{[l]} nH[l]?, n W [ l ] n_W^{[l]} nW[l]?, n C [ l ] n_C^{[l]} nC[l]?
- n H p r e v n_{H_{prev}} nHprev??, n W p r e v n_{W_{prev}} nWprev?? 和 n C p r e v n_{C_{prev}} nCprev??分别表示上一层的高度、宽度和通道数。如果特指某层 l l l,也可以表示为 n H [ l ? 1 ] n_H^{[l-1]} nH[l?1]?, n W [ l ? 1 ] n_W^{[l-1]} nW[l?1]?, n C [ l ? 1 ] n_C^{[l-1]} nC[l?1]?
1 - 导入相关包
让我们首先导入在这个作业中需要的所有包。
numpy是用Python进行科学计算的基本包。
matplotlib是Python中绘制图形的库。
Np.random.seed(1)用于保持所有随机函数调用的一致性。它会帮助我们给你的作业评分
import numpy as np
import h5py
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize']=(5.0, 4.0) #设置图形默认大小
plt.rcParams['image.interpolation']='nearest' #设置最近邻插值
plt.rcParams['image.cmap']='gray' #设置灰色
%load_ext autoreload
%autoreload 2
np.random.seed(1) #设置随机种子
2 - 作业大纲
你将实现一个卷积神经网络的构建模块!你要实现的每个函数都有详细的说明,这些说明将指导你完成所需的步骤:
-
卷积模块,包含:
- Zero Padding 0边界扩充
- Convolve window 卷积窗
- Convolution forward 前向卷积
- Convolution backward (optional) 反向卷积
-
池化模块,包含:
- Pooling forward 前向池化
- Create mask 创建掩码
- Distribute value 值的分配
- Pooling backward (optional) 反向池化
本手册将要求您在numpy中从头开始实现这些函数。在接下来的笔记中,你将使用这些函数的TensorFlow等价形式来构建以下模型:
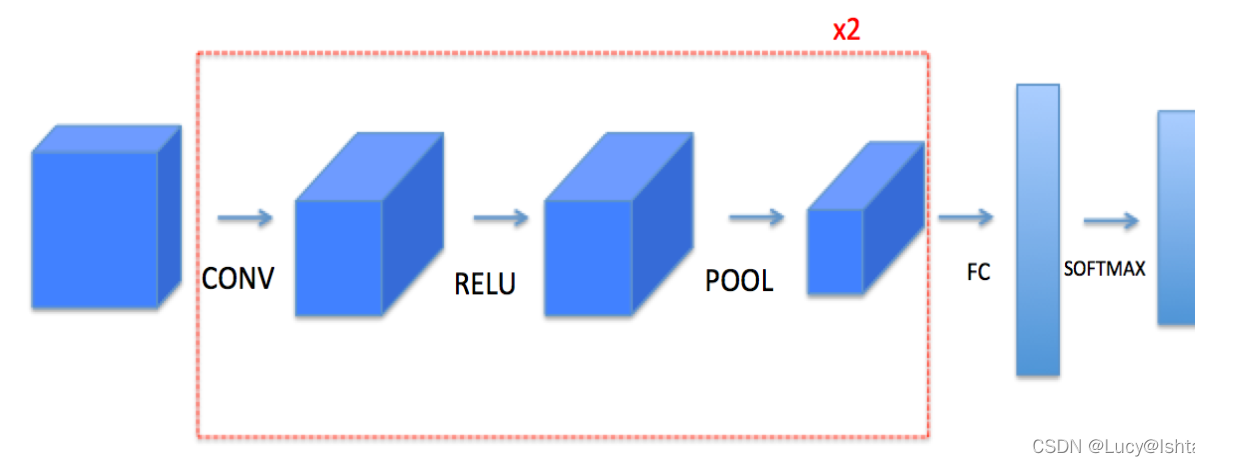
请注意,对于每个正向函数,都有相应的反向等价函数。因此,在前向模块的每一步中,您都将在缓存中存储一些参数。这些参数用于计算反向传播过程中的梯度。
3 - 卷积神经网络
虽然编程框架使卷积易于使用,但它们仍然是深度学习中最难理解的概念之一。卷积层将输入体积转换为不同大小的输出体积,如下所示。
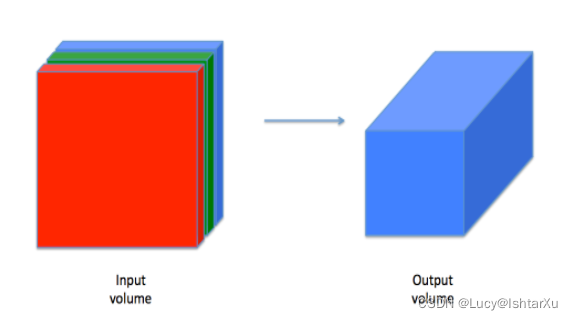
在这一部分中,您将构建卷积层的每一步。您将首先实现两个辅助函数:一个用于零填充,另一个用于计算卷积函数本身
3.1 - 零填充
零填充在图像的边界周围添加0:
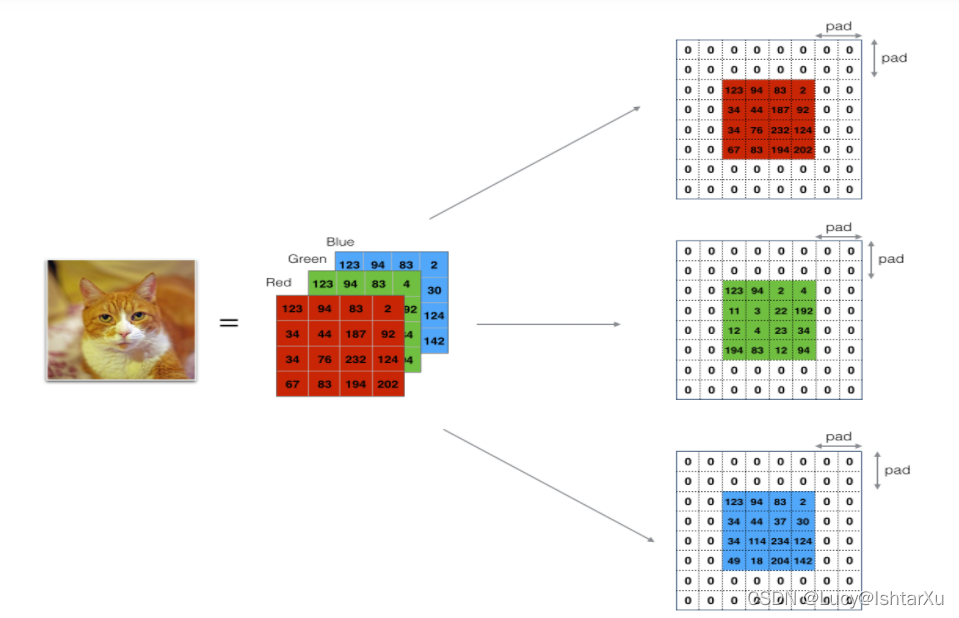

Image (3 channels, RGB) with a padding of 2.
填充的主要好处如下:
- 它允许您使用一个CONV层,而不必缩小高度和宽度的体积。这对于构建更深层次的网络很重要,因为如果不这样,高度/宽度会随着你进入更深层次而缩小。一个重要的特殊情况是same卷积,其中高度/宽度完全保留。
- 它帮助我们在图像的边缘保留更多的信息。没有填充,下一层的值很少会像图像的边缘一样受到像素的影响。
练习:实现以下函数,将一批样本X的所有图像填充为0。使用np.pad。注意,如果你想填充形状(5,5,5,5,5)的数组“a”,第2维的pad = 1,第4维的pad = 3,其余的pad = 0,你会这样做:
参考大佬博客:Numpy学习——数组填充np.pad()函数的应用
a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), 'constant', constant_values = (..,..))
# GRADED FUNCTION: zero_pad
def zero_pad(X, pad):
"""
用0填充数据集X的所有图像,适用于一个图像的高度和宽度,
如图1所示。
参数:
X -- 形状为(m, n_H, n_W, n_C)的python numpy array,代表了一批图像
pad -- 整数,垂直和水平尺寸上每个图像周围的填充量
Returns:
X_pad -- 形状为 (m, n_H + 2*pad, n_W + 2*pad, n_C)的填充图像
"""
### START CODE HERE ### (≈ 1 line)
X_pad = np.pad(X, ((0,0), (pad,pad), (pad,pad), (0,0)), 'constant', constant_values=0 )
### END CODE HERE ###
return X_pad
np.random.seed(1)
x = np.random.randn(4,3,3,2)
x_pad = zero_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_pad.shape =", x_pad.shape)
print ("x[1,1] =", x[1,1])
print ("x_pad[1,1] =", x_pad[1,1])
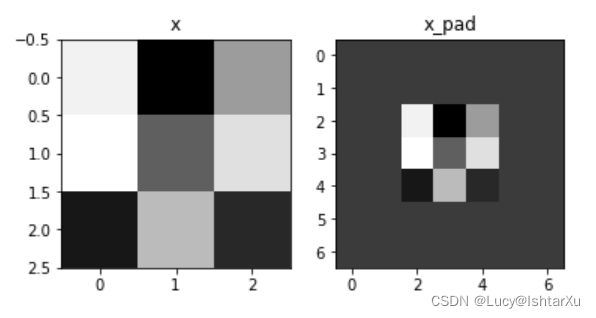
fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])
关于绘图:python 可视化:fig, ax = plt.subplots()画多表图的3中常见样例 & 自定义图表格式
输出结果:
x.shape = (4, 3, 3, 2)
x_pad.shape = (4, 7, 7, 2)
x[1,1] = [[ 0.90085595 -0.68372786]
[-0.12289023 -0.93576943]
[-0.26788808 0.53035547]]
x_pad[1,1] = [[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]]
<matplotlib.image.AxesImage at 0x211570264e0>
3.2 - 单步卷积
在这一部分会实现一个简单的卷积步骤,将过滤器应用到输入的某个位置。这将用于构建一个卷积单元,其中:
- 取一个输入层(体,Volume)
- 在输入层的每个位置使用过滤器
- 输出另一层(通常大小不同)

大小为2x2的过滤器,步长为1 (Stride = 每次滑动时移动窗口的数量)
在计算机视觉应用程序中,左边矩阵中的每一个值对应一个像素值,我们将一个3x3的过滤器与图像进行卷积,方法是将其元素值与原始矩阵相乘,然后将它们相加。在这个练习的第一步中,您将实现一个卷积步骤,只对其中一个位置应用一个过滤器以获得单个实值输出。
在本手册的后面部分,您将对输入的多个位置应用这个函数来实现完整的卷积操作。
【练习】:实现conv_single_step()。提示
# GRADED FUNCTION: conv_single_step
def conv_single_step(a_slice_prev, W, b):
"""
在上一层输出激活的单个切片(a_slice_prev)上应用由参数W定义的一个过滤器。
Arguments:
a_slice_prev -- 输入数据切片的形状(f, f, n_C_prev)
W -- 权重参数 - 矩阵形状 (f, f, n_C_prev)
b -- 偏置参数 - 矩阵形状 (1, 1, 1)
Returns:
Z -- 一个标量值,滑动窗口(W, b)在输入数据的切片x上卷积的结果
"""
### START CODE HERE ### (≈ 2 lines of code)
# a_slice和W之间的元素乘积加偏置
s = np.multiply(a_slice_prev, W) + b
# 对Volume s的所有项求和
Z = np.sum(s)
### END CODE HERE ###
return Z
np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)
Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)
输出结果
Z = -23.16021220252078
3.3 - 卷积神经网络-前向传播
在前向传播中,您将使用许多过滤器并将它们与输入进行卷积。每个“卷积”都给你一个2D矩阵输出。然后将这些输出叠加起来,得到一个3D Volume。
【练习】:实现以下函数,在输入激活A_prev上对过滤器W进行卷积。该函数将前一层的激活输出A_prev(对于一批m个输入)、F滤波器/权重(W)和一个偏置向量(b)作为输入,其中每个滤波器都有自己的(单个)偏置。最后,您还可以访问包含stride和padding的超参数字典。