一、线性支持向量机
1.概念
? ? ? ? 样本：
? ? ? ? 线性分类器：
，
? ? ? ? ?超平面：
?2.函数间隔
????????对于一样训练样本
，它到
确定的超平面的函数间隔为：
????????对于训练数据集
，它的函数间隔定义为
?
3.几何间隔
?
?4.最优间隔分类器
?????????给定一个训练集，试图找到一个使几何间隔最大化的决策边界，这表示对训练集的有可信的预测并且对训练数据的良好“拟合”。
问题转换：令
，
?5.线性SVM
?????????输入：线性可分的训练数据集
???????? 输出：判别函数及决策/判别界面
????????通过求解如下最优化问题来得到最优分类器的参数
?
????????分离超平面:
????????判别函数 :
?6.支持向量和间隔
????????支持向量：距分离超平面最近的训练样本。
????????函数间隔:
????????几何间隔: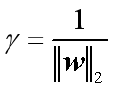
????????间隔:
7.拉格朗日对偶
????????原问题：
? ? ? ? ?约束条件：
? ? ? ? KKT对偶互补条件：
? ? ? ? 对偶问题：
8.线性可分SVM（对偶）
?????????输入 : 线性可分的训练数据集
????????输出 : 分离超平面和判别函数
? ? ? ? 通过求解对偶问题来得到最优解
????????
????????得到原问题的最优解
：
? ? ? ? ?分离超平面：
，判别函数：
二、软间隔分类器
1.软间隔SVM原问题
????????允许一些样本（离群点或噪声样本）违反原来的不等式约束条件：
，但是数目要少。
? ? ? ? 目标函数：
? ? ? ? 替代损失：hinge损失：lhinge(z)=max(0,1-z)
? ? ? ? ? ? ? ? ? ? ? ? ? 指数损失: lexp(z)= exp(-z)
.? ? ? ? ? ? ? ? ? ? ? ? ?对率损失(logistic): llog(z)=log(1+exp(-z))
????????Hinge 损失：?
????????松弛变量
：?
? ? ? ? 拉格朗日函数：
? ? ? ? 对偶问题：
2.非线性可分SVM（对偶问题）
????????输入： 训练数据集?
????????输出 : ?分类超平面与分类决策函数
????????选择参数C ，并求解对偶问题，得最优解
?????????
????????求解最优的
：
? ? ? ? 分类超平面:?
，判别函数:：
????????KKT对偶互补条件：
，即
3.非线性SVM-核方法
? ? ? ? 核函数：使得存在一个函数 K(),对于任意的xi, xj,都有
????????核技巧: 学习与预测时只需使用
????????SVM对偶问题：
? ? ? ??分离超平面及最大间隔分类器：
? ? ? ? ?学习过程是在映射后的特征空间进行的，核函数优势：线性方法来解决非线性问题。
4.常用核函数
????????多项式核:
?????????p =2 ，x=(x1,x2)，
????????映射函数:
????????多项式分类器：
? ? ? ? ?高斯核：
?????????径向基函数：
三、序列最小优化算法（SMO，启发式、迭代式算法）
????????SMO可以高效求解SVM对偶问题。
? ? ? ? SMO动机：坐标梯度上升
????????无约束最优化问题：
????????坐标上升优化算法：
? ? ? ? 坐标梯度下降求解：
????????Repeat until convergence : {
????????（1）选择要更新的一对变量
和
（启发式选择：选择使目标函数值改变最大的变量）
? ? ? ? ?(2) 关于变量?和优化目标函数
? ? ? ? ?假定
满足约束条件，固定
，关于变量
和
优化目标函数：
? ? ? ? 约束条件：
?????????变量的选择方法：第一个变量：违背KKT条件程度最大的变量；第二个变量：使目标函数值减小最快的变量。
SMO算法
输入：训练数据集?
，误差
；
输出：
- ?初始化
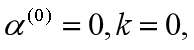，计算偏移量b(0) - 初始化误差项
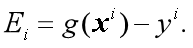
- 选择待优化的变量：
，求解优化问题的解
- 更新
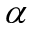为
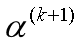，更新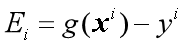
，计算b(k+1) - 如果达到终止条件（满足KKT条件或误差项均小于），则停止算法；否则k=k+1，转到第3步
?四、支持向量回归
????????SVM：
????????回归问题：均方误差损失
? ? ? ? SVC：
? ? ? ? 性质：1.误差在
内，可以接受。即
不敏感损失。2.误差大于
时，对于损失的影响是线性的（不是二次的），对噪声更鲁棒。
? ? ? ? SVR原问题：
? ? ? ? 松弛向量：
其中
为正偏移，
为负偏移
? ? ? ? 带松弛变量的SVR原问题：
? ? ? ? SVR对偶问题：
? ? ? ? KKT条件：
? ? ? ? 多类SVM：训练数据：
? ? ? ? ? ? ? ? ? ? ? ? 最优化问题：
1.相关概念
?????????给定训练数据集
，如果对于任何一个可能的label 集合，都能够从假设空间H中找到找到一个假设h，将训练数据正确地分开，那么就称H打散(shatter) S。
????????对于给定的假设空间H，H能打散的最大的训练数据集中的样本的数目称为H的VC维，记为VC(H)，它度量假设类H的学习能力。
???????