[人工智能]挖掘建模②—聚类分析(包括相关性分析、雷达图等)及python实现

聚类分析

常用聚类方法如下表：

常用聚类算法如下表：

K-Means聚类算法

• K-Means算法是典型的基于距离的非层次聚类算法，在最小化误差函数的基础上将数据划分为预定的类数K，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。
• K-Means聚类算法中，一般需要度量样本之间的距离、样本与簇之间的距离以及簇与簇之间的距离。
  

算法过程

1. 从N个样本数据中随机选取K个对象作为初始的聚类中心；
2. 分别计算每个样本到各个聚类中心的距离，将对象分配到距离最近的聚类中；
3. 所有对象分配完成后，重新计算K个聚类的中心；
4. 与前一次计算得到的K个聚类中心比较，如果聚类中心发生变化，转2)，否则转5；
5. 当质心不发生变化时停止并输出聚类结果。

聚类的结果可能依赖于初始聚类中心的随机选择，可能使得结果严重偏离全局最优分类。实践中，为了得到较好的结果，通常选择不同的初始聚类中心，多次运行K-Means算法。在所有对象分配完成后，重新计算K个聚类的中心时，对于连续数据，聚类中心取该簇的均值，但是当样本的某些属性时分类变量是，均值可能无定义，可以使用K-众数方法。

数据类型与相似性的度量

连续属性

文档数据

目标函数

Python实现

简单实践（仅数值型数据）

部分餐饮客户的消费行为特征数据,consumption_data,根据这些数据将客户分类成不同客户群，并评价这些客户群的价值。

采用K-Means聚类算法，设定聚类个数K为3，最大迭代次数为500次，距离函数取欧氏距离。输出结果如下表

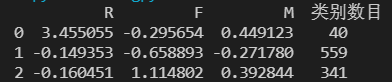
以下是用Pandas和Matplotlib绘制的不同客户分群的概率密度函数图，通过这些图能直观地比较不同客户群的价值。
分群 1 的概率密度函数图：

分群1特点：R间隔相对较小，主要集中在0_{30天之间；消费次数集中在10}25次；消费金额在500~2000。

分群 2的概率密度函数图：

分群2特点：R间隔分布在0-30天之间；消费次数集中在0-12次；消费金额在0-1800。

分群 3的概率密度函数图：

分群3特点：R间隔相对较大，间隔分布在30-80天之间；消费次数集中在0-15次；消费金额在0-2000。

对比分析：分群1时间间隔较短，消费次数多，而且消费金额较大，是高消费高价值人群。分群2的时间间隔、消费次数和消费金额处于中等水平，代表着一般客户。分群3的时间间隔较长，消费次数较少，消费金额也不是特别高，是价值较低的客户群体。

data_type

import pandas as pd
import matplotlib.pyplot as plt  # 导入图像库
from sklearn.cluster import KMeans
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# 参数初始化
inputfile = 'data/consumption_data.xls'  # 销量及其他属性数据
outputfile = 'tmp/data_type.xls'  # 保存结果的文件名
# inputfile = 'tmp/sport.csv'
# outputfile = 'tmp/sport_kmeans.xls' #降维后的数据
k = 3  # 聚类的类别
iteration = 500  # 聚类最大循环次数
data = pd.read_excel(inputfile, index_col='Id')  # 读取数据

data_zs = 1.0*(data - data.mean())/data.std()  # 数据标准化

model = KMeans(n_clusters=k,  max_iter=iteration)  # 分为k类
model.fit(data_zs)  # 开始聚类

# 简单打印结果
r1 = pd.Series(model.labels_).value_counts()  # 统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_)  # 找出聚类中心
r = pd.concat([r2, r1], axis=1)  # 横向连接（0是纵向），得到聚类中心对应的类别下的数目
r.columns = list(data.columns) + [u'类别数目']  # 重命名表头
print(r)

# 详细输出原始数据及其类别
# 详细输出每个样本对应的类别
r = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)
r.columns = list(data.columns) + [u'聚类类别']  # 重命名表头
r.to_excel(outputfile)  # 保存结果
def density_plot(data,k):  # 自定义作图函数
    p = data.plot(kind='kde', linewidth=2, subplots=True, sharex=False)
    [p[i].set_ylabel(u'密度') for i in range(k)]
    plt.legend()
    return plt
pic_output = 'tmp/pd_'  # 概率密度图文件名前缀
for i in range(k):
    density_plot(data[r[u'聚类类别'] == i],k).savefig(
        u'%s%s.png' % (pic_output, i))

较复杂实践（数值型数据及分类数据）

导入数据，引用包

import pandas as pd  # 导入数据分析库Pandas
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt  # 导入图像库
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder  # 文本向量化
from sklearn.preprocessing import MinMaxScaler  # 数据标准化
from sklearn.cluster import KMeans  # 聚类算法模型
from sklearn.metrics import silhouette_score  # 轮廓系数

def density_plot(data,k):  # 自定义作图函数
    p = data.plot(kind='kde', linewidth=2, subplots=True, sharex=False)
    [p[i].set_ylabel(u'密度') for i in range(k)]
    plt.legend()
    return plt
inputfile = 'tmp/sport.csv'
outputfile = 'tmp/sport_kmeans.xls' #降维后的数据
raw_data = pd.read_csv(inputfile)  # 读取数据
raw_data=raw_data[["学号","年级代码","学院","体重指数", "肺活量", "一分钟仰卧起坐", "坐位体前屈", "立定跳远", "800米秒"]]
raw_data[['年级代码']] = raw_data[['年级代码']].astype(str)  # 转字符串
raw_data[['学号']] = raw_data[['学号']].astype(str)  # 转字符串
raw_data.head()
numbercols=["体重指数", "肺活量", "一分钟仰卧起坐", "坐位体前屈", "立定跳远", "800米秒"]
classcols=[ "学院"]

查看基本状态

# 查看基本状态
print('{:*^60}'.format('数据前两行:'))
print(raw_data.head(2))  # 打印输出前2条数据

print('{:*^60}'.format('数据类型:'))
print(pd.DataFrame(raw_data.dtypes).T)  # 打印数据类型分布

print('{:*^60}'.format('数据统计描述:'))
print(raw_data.describe().round(2).T)  # 打印原始数据基本描述性信息

缺失值审查

# 缺失值审查
na_cols = raw_data.isnull().any(axis=0)  # 查看每一列是否具有缺失值
print('{:*^60}'.format('含有缺失值的列:'))
print(na_cols[na_cols==True])  # 查看具有缺失值的列
print('总共有多少数据缺失: {0}'.format(raw_data.isnull().any(axis=1).sum()))  # 查看具有缺失值的行总记录数

相关性分析

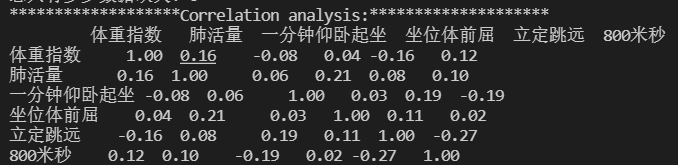
# 相关性分析
print('{:*^60}'.format('Correlation analysis:'))
print(raw_data.corr().round(2).T)  # 打印原始数据相关性信息

ylabels = raw_data[numbercols].columns.values.tolist()
plt.subplots(figsize=(15, 10))  # 设置画面大小
sns.heatmap(raw_data[numbercols].corr(), annot=True, vmax=1, square=True,
            yticklabels=ylabels, xticklabels=ylabels, cmap="RdBu")

# 类别变量取值

for x in classcols:
    data=raw_data[x].unique()
    print("变量【{0}】的取值有：\n{1}".format(x,data))
    print("-·"*20)

# 字符串分类独热编码处理
model_ohe = OneHotEncoder(sparse=False)  # 建立OneHotEncode对象
ohe_matrix = model_ohe.fit_transform(raw_data[classcols])  # 直接转换
print(ohe_matrix[:2])

# 用pandas的方法
ohe_matrix1=pd.get_dummies(raw_data[classcols])
ohe_matrix1.head(5)

# 数据标准化
sacle_matrix = raw_data[numbercols] # 获得要转换的矩阵
model_scaler = MinMaxScaler()  # 建立MinMaxScaler模型对象
data_scaled = model_scaler.fit_transform(sacle_matrix)  # MinMaxScaler标准化处理
print(data_scaled.round(2))

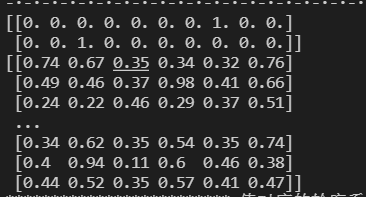
# 合并所有维度
X = np.hstack((data_scaled, ohe_matrix))


# 通过平均轮廓系数检验得到最佳KMeans聚类模型
score_list = list()  # 用来存储每个K下模型的平局轮廓系数
silhouette_int = -1  # 初始化的平均轮廓系数阀值
for n_clusters in range(2, 5):  # 遍历从2到5几个有限组
    model_kmeans = KMeans(n_clusters=n_clusters)  # 建立聚类模型对象
    labels_tmp = model_kmeans.fit_predict(X)  # 训练聚类模型
    silhouette_tmp = silhouette_score(X, labels_tmp)  # 得到每个K下的平均轮廓系数
    if silhouette_tmp > silhouette_int:  # 如果平均轮廓系数更高
        best_k = n_clusters  # 保存K将最好的K存储下来
        silhouette_int = silhouette_tmp  # 保存平均轮廓得分
        best_kmeans = model_kmeans  # 保存模型实例对象
        cluster_labels_k = labels_tmp  # 保存聚类标签
    score_list.append([n_clusters, silhouette_tmp])  # 将每次K及其得分追加到列表
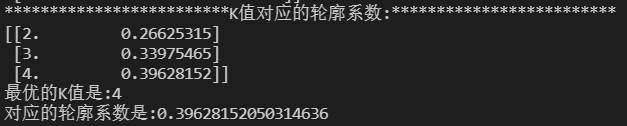
print('{:*^60}'.format('K值对应的轮廓系数:'))
print(np.array(score_list))  # 打印输出所有K下的详细得分
print('最优的K值是:{0} \n对应的轮廓系数是:{1}'.format(best_k, silhouette_int))

 # 详细输出每个样本对应的类别
r = pd.concat([raw_data, pd.Series(best_kmeans.labels_, index=raw_data.index)], axis=1)
r.columns = list(raw_data.columns) + [u'聚类类别']  # 重命名表头
r.to_excel(outputfile)  # 保存结果
# 各类别字段概率密度图
pic_output = 'tmp/pd_'  # 概率密度图文件名前缀
for i in range(best_k):
    density_plot(raw_data[r[u'聚类类别'] == i],len(numbercols)).savefig(
    u'%s%s.png' % (pic_output, i))
        

# 将原始数据与聚类标签整合
cluster_labels = pd.DataFrame(cluster_labels_k, columns=['clusters'])  # 获得训练集下的标签信息
merge_data = pd.concat((raw_data, cluster_labels), axis=1)  # 将原始处理过的数据跟聚类标签整合
merge_data.head()


# 计算每个聚类类别下的样本量和样本占比
clustering_count = pd.DataFrame(merge_data['学号'].groupby(merge_data['clusters']).count()).T.rename({'学号': 'counts'})  # 计算每个聚类类别的样本量
clustering_ratio = (clustering_count / len(merge_data)).round(2).rename({'counts': 'percentage'})  # 计算每个聚类类别的样本量占比
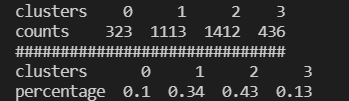
print(clustering_count)
print("#"*30)
print(clustering_ratio)

# 计算各个聚类类别内部最显著特征值
cluster_features = []  # 空列表，用于存储最终合并后的所有特征信息
for line in range(best_k):  # 读取每个类索引
    label_data = merge_data[merge_data['clusters'] == line]  # 获得特定类的数据

    part1_data = label_data[numbercols] # 获得数值型数据特征
    part1_desc = part1_data.describe().round(3)  # 得到数值型特征的描述性统计信息
    merge_data1 = part1_desc.iloc[2, :]  # 得到数值型特征的均值

    part2_data = label_data[classcols]  # 获得字符串型数据特征
    part2_desc = part2_data.describe(include='all')  # 获得字符串型数据特征的描述性统计信息
    merge_data2 = part2_desc.iloc[2, :]  # 获得字符串型数据特征的最频繁值

    merge_line = pd.concat((merge_data1, merge_data2), axis=0)  # 将数值型和字符串型典型特征沿行合并
    cluster_features.append(merge_line)  # 将每个类别下的数据特征追加到列表

#  输出完整的类别特征信息
cluster_pd = pd.DataFrame(cluster_features).T  # 将列表转化为矩阵
print('{:*^60}'.format('每个类别主要的特征:'))
all_cluster_set = pd.concat((clustering_count, clustering_ratio, cluster_pd),axis=0)  # 将每个聚类类别的所有信息合并
print(all_cluster_set)

#各类别数据预处理
num_sets = cluster_pd.iloc[:6, :].T.astype(np.float64)  # 获取要展示的数据
num_sets_max_min = model_scaler.fit_transform(num_sets)  # 获得标准化后的数据
print('-'*60)
print(num_sets_max_min)

# 画图
fig = plt.figure(figsize=(6,6))  # 建立画布
ax = fig.add_subplot(111, polar=True)  # 增加子网格，注意polar参数
labels = np.array(merge_data1.index)  # 设置要展示的数据标签
cor_list = ['g', 'r', 'y', 'b','o','PuRd','YlGnBu']  # 定义不同类别的颜色
angles = np.linspace(0, 2 * np.pi, len(labels), endpoint=False)  # 计算各个区间的角度
angles = np.concatenate((angles, [angles[0]]))  # 建立相同首尾字段以便于闭合
# 画雷达图
for i in range(len(num_sets)):  # 循环每个类别
    data_tmp = num_sets_max_min[i, :]  # 获得对应类数据
    data = np.concatenate((data_tmp, [data_tmp[0]]))  # 建立相同首尾字段以便于闭合
    ax.plot(angles, data, 'o-', c=cor_list[i], label="第%d类学生"%(i))  # 画线
    ax.fill(angles, data,alpha=0.5)
# 设置图像显示格式
ax.set_thetagrids(angles * 180 / np.pi, labels, fontproperties="SimHei")  # 设置极坐标轴
ax.set_title("各聚类类别显著特征对比", fontproperties="SimHei")  # 设置标题放置
ax.set_rlim(-0.2, 1.2)  # 设置坐标轴尺度范围
plt.legend(loc="upper right" ,bbox_to_anchor=(1.2,1.0))  # 设置图例位置
# plt.savefig(u'a.png' )
plt.show()