[人工智能]通过深度神经网络和树搜索掌握围棋游戏

Article

作者：David Silver*, Aja Huang*, Chris J. Maddison etc.
文献题目：通过深度神经网络和树搜索掌握围棋游戏
文献时间：2016
发表期刊：nature
https://github.com/jmgilmer/GoCNN

摘要

• 由于其巨大的搜索空间和评估棋盘位置和移动的难度，围棋一直被视为人工智能经典游戏中最具挑战性的游戏。在这里，我们介绍了一种新的计算机围棋方法，它使用“价值网络”来评估棋盘位置和“策略网络”来选择走法。这些深度神经网络通过人类专家游戏的监督学习和自我游戏的强化学习的新颖组合进行训练。在没有任何前瞻搜索的情况下，神经网络在最先进的蒙特卡罗树搜索程序的水平上下围棋，模拟数千个随机的自我游戏。我们还介绍了一种新的搜索算法，它将蒙特卡罗模拟与价值和策略网络相结合。使用这种搜索算法，我们的程序 AlphaGo 对其他围棋程序取得了 99.8% 的胜率，以 5 比 0 击败了人类欧洲围棋冠军。 这是计算机程序首次全面击败人类职业棋手围棋，以前认为至少需要十年才能实现这一壮举。

• 所有完美信息博弈都有一个最优值函数 $v^{?}(s)$，它决定了在所有玩家完美玩的情况下，每个棋盘位置或状态 $s$ 的博弈结果。这些游戏可以通过在包含大约 $b^d$ 个可能的移动序列的搜索树中递归计算最优值函数来解决，其中 $b$ 是游戏的广度（每个位置的合法移动数），$d$ 是其深度（游戏长度）。在大型游戏中，例如国际象棋$(b\approx 35,d\approx 80)$，尤其是围棋$(b\approx 250,d\approx 150)$，穷举搜索是不可行的，但可以通过两个一般原则减少有效搜索空间。首先，搜索的深度可以通过位置评估来减少：截断状态 $s$ 处的搜索树，并用一个近似值函数 $v(s)\approx v^{?}(s)$ 替换 $s$ 下方的子树，该函数可以预测状态 $s$ 的结果。这种方法在国际象棋、跳棋和黑白棋中取得了超人的表现，但由于游戏的复杂性，人们认为它在围棋中难以驾驭。其次，可以通过从策略 $p(a|s)$ 中采样动作来减少搜索的广度，策略 $p(a|s)$ 是位置 $s$ 中可能移动 $a$ 的概率分布。例如，蒙特卡罗通过从策略 $p$ 中对两个玩家的长动作序列进行采样，在完全不分支的情况下搜索到最大深度。对此类推出进行平均可以提供有效的位置评估，在西洋双陆棋和拼字游戏中实现超人的表现，在围棋中实现弱的业余水平。

• Monte Carlo 树搜索 (MCTS) 使用 Monte Carlo rollouts 来估计搜索树中每个状态的值。 随着执行更多的模拟，搜索树变得更大，相关值变得更准确。 通过选择具有更高值的子项，用于在搜索期间选择操作的策略也随着时间的推移而改进。 渐近地，该策略收敛到最优玩法，并且评估收敛到最优值函数。 当前最强大的围棋程序基于 MCTS，并通过经过训练以预测人类专家动作的策略得到增强。 这些策略用于将搜索范围缩小到一系列高概率动作，并在推出期间对动作进行采样。 这种方法已经实现了强大的业余发挥。 然而，先前的工作仅限于基于输入特征的线性组合的浅层策略或价值函数。

• 我们使用由机器学习的几个阶段组成的pipeline来训练神经网络（图 1）。 我们首先直接从专家人类动作训练监督学习 (SL) 策略网络 $p_{\sigma }$。 这通过即时反馈和高质量梯度提供快速、高效的学习更新。 与之前的工作类似，我们还训练了一个快速策略 $p_{\pi }$，可以在部署期间快速采样动作。 接下来，我们训练一个强化学习 (RL) 策略网络 $p_{\rho }$，它通过优化自我博弈的最终结果来改进 SL 策略网络。 这会朝着赢得比赛的正确目标调整策略，而不是最大化预测准确性。 最后，我们训练了一个价值网络 $v_{\theta }$，它可以预测 RL 策略网络与自身进行的游戏的获胜者。 我们的程序 AlphaGo 将策略和价值网络与 MCTS 有效地结合在一起。
  

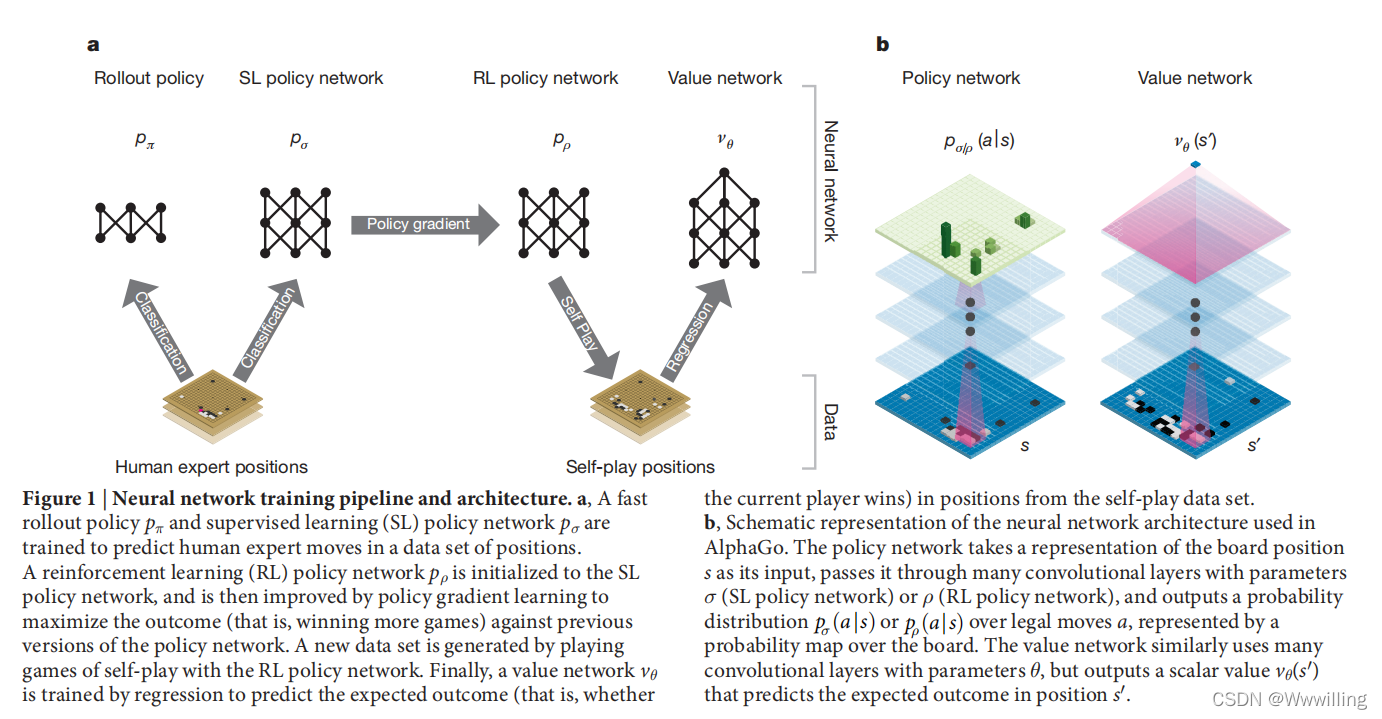
• 图1 |神经网络训练管道和架构。
  a，训练快速推出策略 $p_{\pi }$ 和监督学习 (SL) 策略网络 $p_{\sigma }$ 来预测人类专家在位置数据集中的移动。强化学习 (RL) 策略网络 $p_{\rho }$ 被初始化为 SL 策略网络，然后通过策略梯度学习进行改进，以最大化对抗先前版本的策略网络的结果（即赢得更多游戏）。一个新的数据集是通过与 RL 策略网络进行自我博弈而生成的。最后，通过回归训练价值网络 $v_{\theta }$，以预测自我对弈数据集中位置的预期结果（即当前玩家是否获胜）。
  b，AlphaGo 中使用的神经网络架构的示意图。策略网络将棋盘位置 $s$ 的表示作为其输入，将其通过参数为 $\sigma$（SL 策略网络）或 $\rho$（RL 策略网络）的许多卷积层，并输出概率分布 $p_{\sigma }(a|s)$ 或 $p_{\rho }(a|s)$ 通过合法移动 $a$，由棋盘上的概率图表示。价值网络类似地使用许多具有参数 $\theta$ 的卷积层，但输出一个标量值 $v_{\theta }(s^{\prime })$ 来预测位置 $s^{\prime }$ 的预期结果。

策略网络的监督学习

• 对于训练管道的第一阶段，我们建立在使用监督学习预测围棋游戏中专家动作的先前工作的基础上。 SL 策略网络 $p_{\sigma }(a|s)$ 在权重为 $\sigma$ 的卷积层和整流器非线性之间交替。 最后一个 softmax 层输出所有合法移动 $a$ 的概率分布。 策略网络的输入 $s$ 是董事会状态的简单表示（参见扩展数据表 2）。 策略网络在随机采样的状态-动作对 $(s,a)$ 上进行训练，使用随机梯度上升来最大化在状态 $s$ 中选择的人类移动 $a$ 的可能性。
  
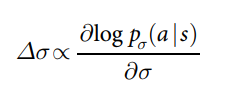
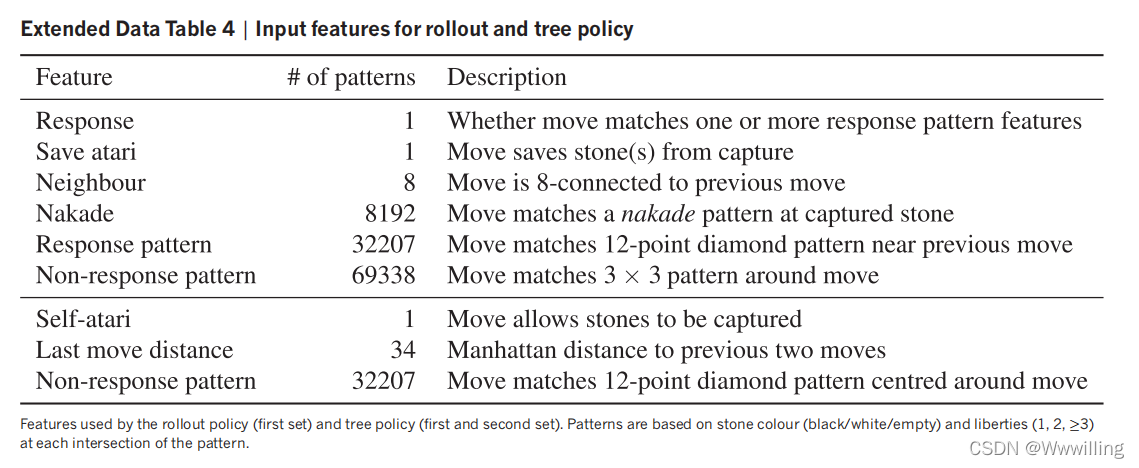
• 我们从 KGS Go Server 的 3000 万个位置训练了一个 13 层的策略网络，我们称之为 SL 策略网络。 与最新技术相比，网络预测专家在保留的测试集上移动，使用所有输入特征的准确率为 57.0%，仅使用原始棋盘位置和移动历史作为输入的准确率为 55.7% 来自其他研究小组的 44.4% 在提交之日（扩展数据表 3 中的完整结果）。 准确性的小幅提升导致演奏强度的大幅提升（图 2a）； 更大的网络可以获得更好的准确性，但在搜索过程中评估速度较慢。 我们还使用权重为 π 的小模式特征的线性 softmax（参见扩展数据表 4）训练了一个更快但不太准确的 rollout 策略 $p_{\pi }(a|s)$； 这实现了 24.2% 的准确率，仅使用 2μs 来选择一个动作，而不是策略网络的 3ms。
  
  
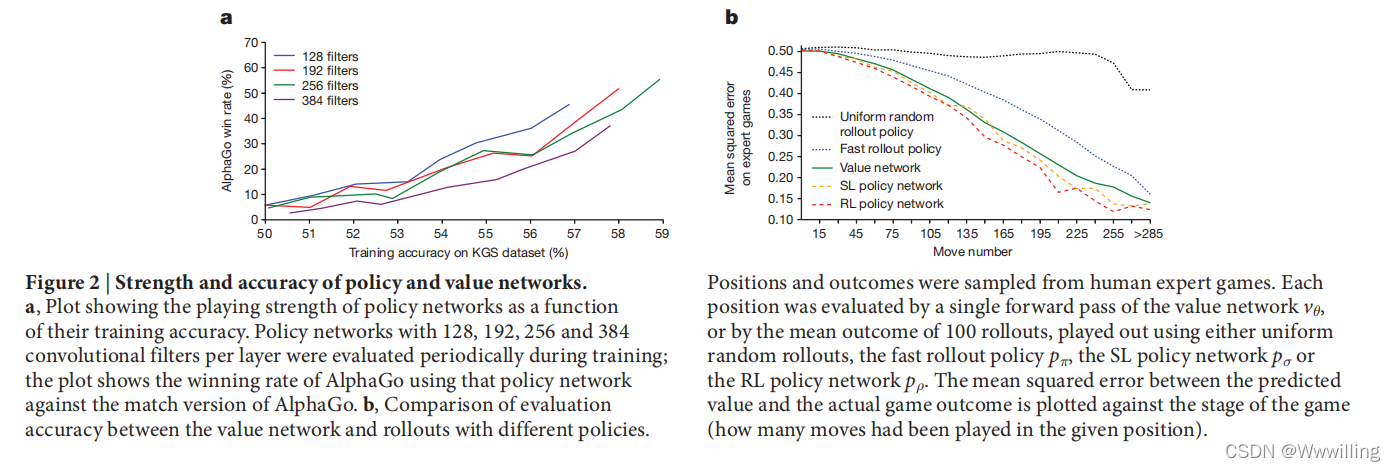
• 图2 | 策略和价值网络的强度和准确性。
  a，显示策略网络的播放强度作为其训练准确性的函数的图。 在训练期间定期评估每层具有 128、192、256 和 384 个卷积滤波器的策略网络； 该图显示了使用该策略网络的 AlphaGo 与匹配版本的 AlphaGo 的获胜率。
  b，价值网络和不同策略的rollouts之间的评估精度比较。 位置和结果是从人类专家游戏中采样的。 每个位置都通过价值网络 $v_{\theta }$ 的单次前向传递进行评估，或通过 100 次 rollout 的平均结果进行评估，使用均匀随机 rollout、快速 rollout 策略 $p_{\pi }$、SL 策略网络 $p_{\sigma }$ 或 RL 策略网络 $p_{\rho }$ 进行评估。 预测值和实际游戏结果之间的均方误差根据游戏阶段（在给定位置进行了多少步）绘制。

策略网络的强化学习

• 训练管道的第二阶段旨在通过策略梯度强化学习 (RL) 改进策略网络。 RL 策略网络 $p_{\rho }$ 在结构上与 SL 策略网络相同，其权重 $\rho$ 被初始化为相同的值，$\rho =\sigma$。 我们在当前策略网络 $p_{\rho }$ 和之前随机选择的策略网络迭代之间玩游戏。 以这种方式从一组对手中随机化通过防止过度拟合当前策略来稳定训练。 我们使用奖励函数 $r(s)$ 对于所有非终端时间步 $t<T$ 为零。 结果 $z_t=\pm r(s_T)$ 是在时间步骤 $t$ 从当前玩家的角度来看，游戏结束时的最终奖励：赢+1，输-1。 然后在每个时间步长 $t$ 通过在最大化预期结果的方向上随机梯度上升来更新权重。
  
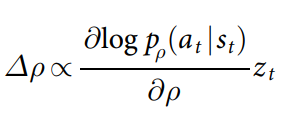
• 我们评估了 RL 策略网络在游戏中的性能，从每个动作的输出概率分布中采样 $a_t～p_{\rho }(?|s_t)$。 当与 SL 策略网络进行正面交锋时，RL 策略网络赢得了 80% 以上的对战 SL 策略网络。 我们还针对最强大的开源围棋程序 Pachi 进行了测试，Pachi 是一个复杂的蒙特卡罗搜索程序，在 KGS 上排名第 2 业余段位，每步执行 100,000 次模拟。 完全不使用搜索，RL 策略网络在与 Pachi 的比赛中赢得了 85% 的胜利。 相比之下，以前的最新技术仅基于监督。
• 相比之下，之前的最新技术仅基于卷积网络的监督学习，在对抗 Pachi 的比赛中赢得了 11% 的胜利，在对抗稍弱的程序 Fuego 的比赛中赢得了 12% 的胜利。

价值网络的强化学习

• 训练管道的最后阶段侧重于位置评估，估计一个价值函数 $v^p(s)$，该函数通过对两个玩家使用策略 $p$ 来预测来自所玩游戏的位置 $s$ 的结果。
  
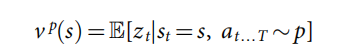
• 理想情况下，我们想知道完美游戏 $v^{?}(s)$ 下的最优值函数； 在实践中，我们使用 RL 策略网络 $p_{\rho }$ 来估计我们最强策略的价值函数 $v^{p_{\rho }}$。 我们使用权重为 $\theta$, $v_{\theta }\left(s\right)\approx v^{p_{\rho }}\left(s\right)\approx v^{?}\left(s\right)$的价值网络 $v_{\theta }(s)$ 来近似价值函数。 该神经网络与策略网络具有相似的架构，但输出的是单个预测而不是概率分布。 我们通过状态-结果对 $(s,z)$ 上的回归来训练价值网络的权重，使用随机梯度下降来最小化预测值 $v_{\theta }(s)$ 和相应结果 $z$ 之间的均方误差 (MSE) 。
  
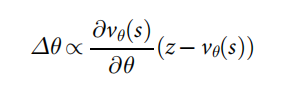
• 从包含完整游戏的数据中预测游戏结果的幼稚方法会导致过度拟合。问题是连续的位置是强相关的，只有一颗石头不同，但整个游戏共享回归目标。当以这种方式在 KGS 数据集上训练时，价值网络记住了比赛结果而不是泛化到新位置，在测试集上实现了 0.37 的最小 MSE，而在训练集上则为 0.19。为了缓解这个问题，我们生成了一个新的自游戏数据集，包含 3000 万个不同的位置，每个位置都从一个单独的游戏中采样。每个游戏都在 RL 策略网络与其自身之间进行，直到游戏终止。对该数据集的训练导致训练集和测试集的 MSE 分别为 0.226 和 0.234，表明过拟合最小。图 2b 显示了价值网络的位置评估精度，与使用快速 rollout 策略 pπ 的 Monte Carlo rollout 相比；价值函数始终更准确。对 $v_{\theta }(s)$ 的单个评估也接近使用 RL 策略网络 $p_{\rho }$ 的 Monte Carlo rollouts 的准确性，但使用的计算量减少了 15,000 倍。

使用策略和价值网络进行搜索

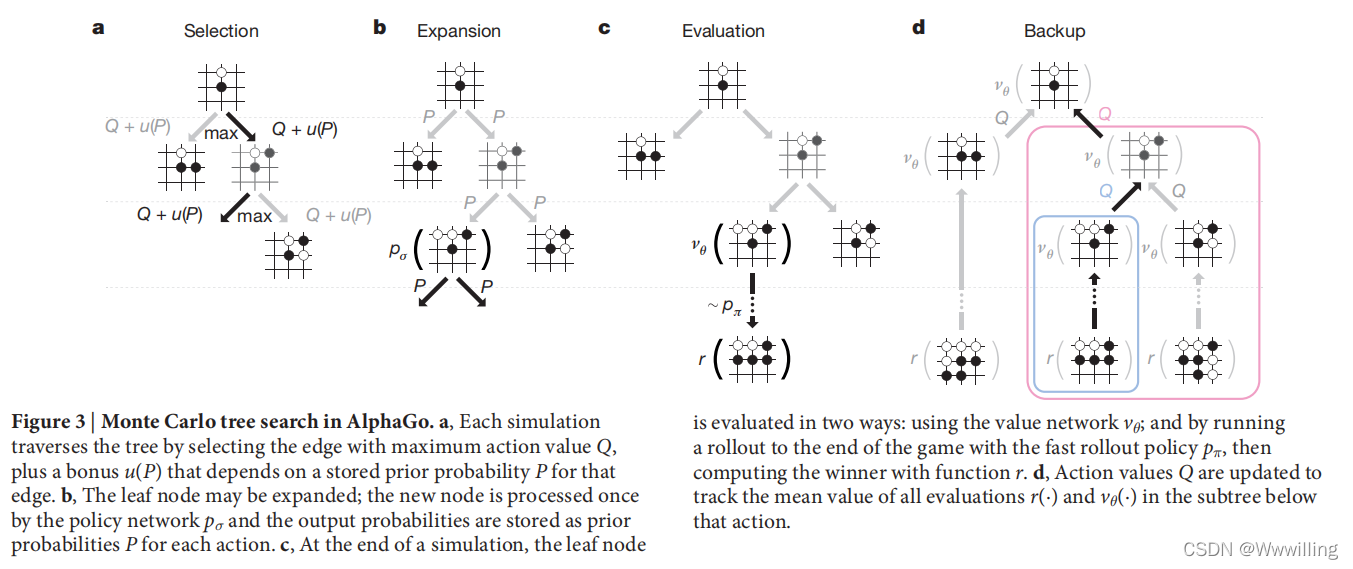
• AlphaGo 在 MCTS 算法（图 3）中结合了策略和价值网络，该算法通过先行搜索来选择动作。
  

• 图 3 | AlphaGo 中的蒙特卡罗树搜索。
  a，每次模拟都通过选择具有最大动作值 $Q$ 的边以及取决于该边存储的先验概率 $P$ 的奖励 $u(P)$ 来遍历树。
  b、叶子节点可以扩展； 新节点由策略网络 $p_{\sigma }$ 处理一次，输出概率存储为每个动作的先验概率 $P$。
  c、在模拟结束时，叶子节点通过两种方式进行评估：使用价值网络$v_{\theta }$； 并通过使用快速推出策略 $p_{\pi }$ 运行推出到游戏结束，然后使用函数 $r$ 计算获胜者。
  d，更新动作值 $Q$ 以跟踪该动作下方子树中所有评估 $r(?)$ 和 $v_{\theta }(?)$ 的平均值。

• 搜索树的每条边 $(s,a)$ 都存储了一个动作值 $Q(s,a)$、访问次数 $N(s,a)$ 和先验概率 $P(s,a)$。 树通过模拟遍历（即在没有备份的完整游戏中下降树），从根状态开始。 在每次模拟的每个时间步长$t$，从状态 $s_t$ 中选择一个动作 $a_t$。
  

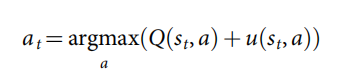
• 从而最大限度地提高行动价值和奖金
  

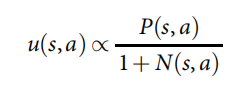
• 这与先验概率成正比，但会随着重复访问而衰减以鼓励探索。 当遍历在步骤 $L$ 到达叶节点 $s_L$ 时，可以扩展叶节点。 SL 策略网络 $p_{\sigma }$ 只处理叶位置 $s_L$ 一次。输出概率作为每个合法行为 $a$ 的先验概率 $P$ 存储, $P(s|a)=P_{\sigma }(a|s)$ 。 叶节点以两种截然不同的方式进行评估：首先，通过价值网络 $v_{\theta }(s_L)$； 其次，根据使用快速推出策略 $p_{\pi }$ 的随机推出的结果 $z_L$，直到终端步骤 $T$ 为止； 使用混合参数 $\lambda$ 将这些评估组合成叶子评估 $V(s_L)$
  

• 在模拟结束时，更新所有遍历边的动作值和访问计数。 每条边累积通过该边的所有模拟的访问计数和平均评估
  

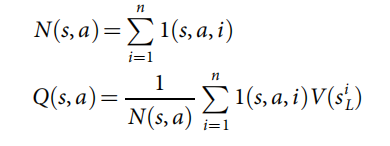
• 其中 ${s_L}^i$ 是第$i$ 次模拟的叶节点，$1(s,a,i)$ 表示在第 $i$ 次模拟期间是否遍历了边 $(s,a)$。 搜索完成后，算法从根位置选择访问量最大的移动。

• 值得注意的是，SL 策略网络 $p_{\sigma }$ 在 AlphaGo 中的表现比更强的 RL 策略网络 $p_{\rho }$ 更好，这大概是因为人类选择了一系列有希望的走法，而 RL 优化了单一的最佳走法。 然而，从更强的 RL 策略网络导出的价值函数 $v_{\theta }\left(s\right)\approx v^{p_{\rho }}\left(s\right)$ 在 AlphaGo 中比从 SL 策略网络导出的价值函数 $v_{\theta }\left(s\right)\approx v^{p_{\sigma }}\left(s\right)$ 表现得更好。

• 评估策略和价值网络需要比传统搜索启发式算法多几个数量级的计算。 为了有效地将 MCTS 与深度神经网络相结合，AlphaGo 使用异步多线程搜索在 CPU 上执行模拟，并在 GPU 上并行计算策略和价值网络。 AlphaGo 的最终版本使用了 40 个搜索线程、48 个 CPU 和 8 个 GPU。 我们还实现了一个分布式版本的 AlphaGo，它利用了多台机器、40 个搜索线程、1,202 个 CPU 和 176 个 GPU。 方法部分提供了异步和分布式 MCTS 的完整详细信息。

评估AlphaGo的棋力

• 为了评估 AlphaGo，我们在 AlphaGo 的变体和其他几个围棋程序之间举办了一场内部比赛，其中包括最强的商业程序 Crazy Stone 和 Zen，以及最强的开源程序 Pachi和 Fuego。 所有这些程序都基于高性能的 MCTS 算法。 此外，我们还包括开源程序 GnuGo，这是一个使用 MCTS 之前的最先进搜索方法的 Go 程序。 所有程序每次移动都允许有 5 秒的计算时间。
• 锦标赛的结果（见图 4a）表明，单机 AlphaGo 比以前的任何围棋程序都要强很多段位，在与其他围棋程序的 495 场比赛中赢了 494 场（99.8%）。 为了给AlphaGo提供更大的挑战，我们还进行了四颗让子（即对手自由走）的对局； AlphaGo 分别以 77%、86% 和 99% 的胜率战胜了 Crazy Stone、Zen 和 Pachi。 AlphaGo 的分布式版本明显更强大，对单机 AlphaGo 的比赛胜率为 77%，与其他程序的比赛胜率为 100%。
• 我们还评估了仅使用价值网络 $(\lambda =0)$ 或仅使用 rollouts $(\lambda =1)$ 评估位置的 AlphaGo 变体（见图 4b）。 即使没有推出，AlphaGo 也超过了所有其他围棋程序的性能，这表明价值网络为围棋中的蒙特卡罗评估提供了可行的替代方案。 然而，混合评估 (λ=0.5) 表现最好，在与其他变体的比赛中获胜率≥95%。 这表明两种位置评估机制是互补的：价值网络近似于强但不切实际的慢 pρ 所玩游戏的结果，而 rollouts 可以精确地评分和评估较弱但较快的 rollout 策略 pπ 玩的游戏的结果 . 图 5 显示了 AlphaGo 对真实游戏位置的评估。
  
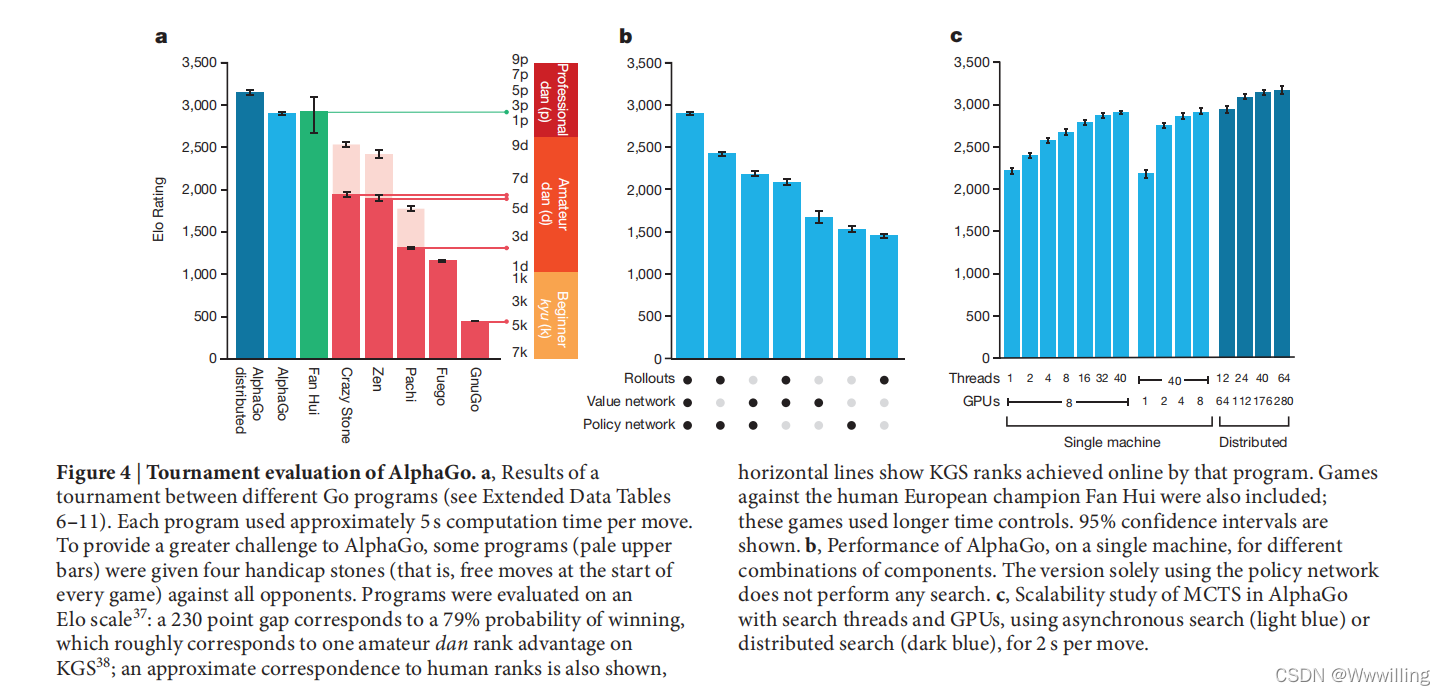
• 图 4 | AlphaGo 的比赛评估。
  a，不同围棋程序之间的比赛结果（参见扩展数据表 6-11）。每个程序每次移动使用大约 5 秒的计算时间。为了向 AlphaGo 提供更大的挑战，一些程序（苍白的上条）被给予四块让步棋（即每场比赛开始时的自由步）对抗所有对手。程序的评估采用 Elo 量表37：230 分的差距对应于 79% 的获胜概率，大致对应于 KGS38 上的一个业余段位优势；还显示了与人类等级的近似对应关系，水平线显示了该程序在线获得的 KGS 等级。与人类欧洲冠军范辉的比赛也包括在内；这些游戏使用了更长的时间控制。显示了 95% 的置信区间。
  b, AlphaGo 在单台机器上，不同组件组合的性能。仅使用策略网络的版本不执行任何搜索。
  c，使用异步搜索（浅蓝色）或分布式搜索（深蓝色），在 AlphaGo 中使用搜索线程和 GPU 进行 MCTS 的可扩展性研究，每步 2 秒。
  
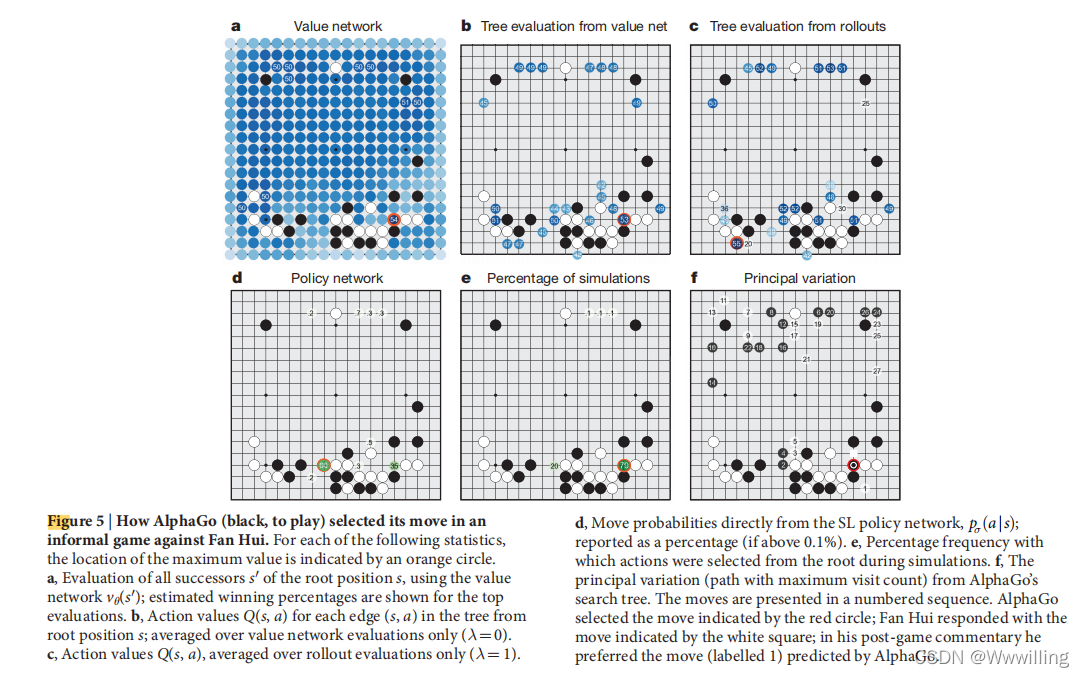
• 图 5 | AlphaGo（黑棋，下棋）在与范辉的非正式游戏中如何选择棋步。对于以下每个统计量，最大值的位置由橙色圆圈表示。
  a, 使用价值网络 $v_{\theta }(s^{\prime })$ 评估根位置 $s$ 的所有后继 $s^{\prime }$；显示最高评价的估计获胜百分比。
  b, 树中从根位置 $s$ 开始的每条边 $(s,a)$ 的动作值 $Q(s,a)$；仅对价值网络评估进行平均 $(\lambda =0)$。
  c，动作值 $Q(s,a)$，仅在 rollout 评估上取平均值 $(\lambda =1)$。
  d，直接从 SL 策略网络移动概率，$p_{\sigma }(a|s)$；报告为百分比（如果高于 0.1%）。
  e，在模拟期间从根中选择动作的百分比频率。
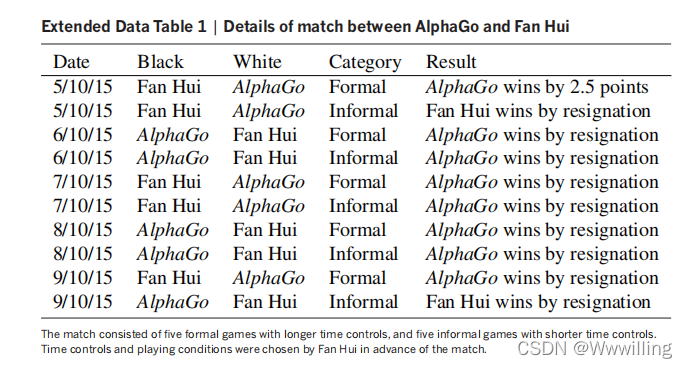
  f，来自 AlphaGo 搜索树的主要变体（具有最大访问次数的路径）。这些动作按编号顺序呈现。 AlphaGo 选择了红色圆圈所示的走法；范辉以白色方块所示的动作回应；在他的赛后评论中，他更喜欢 AlphaGo 预测的走法（标记为 1）。
• 最后，我们将分布式版本的 AlphaGo 与专业 2 段棋手、2013、2014 和 2015 年欧洲围棋锦标赛冠军范慧进行了对比。 2015 年 10 月 5 日至 9 日，AlphaGo 和范慧进行了一场正式的五局比赛。 AlphaGo 以 5 比 0 赢得比赛（图 6 和扩展数据表 1）。 这是计算机围棋程序第一次在完整的围棋比赛中无障碍地击败人类职业棋手——此前人们认为这一壮举至少需要十年时间才能实现。
  
• 图 6 | AlphaGo 与欧洲冠军范慧的比赛。
  移动按与它们播放的顺序相对应的编号顺序显示。 在同一交叉点上的重复移动在棋盘下方成对显示。 每对中的第一个移动编号指示重复移动的时间，在由第二个移动编号标识的交叉点处（参见补充信息）。
  

讨论

• 在这项工作中，我们开发了一个基于深度神经网络和树搜索的组合的围棋程序，它在最强的人类玩家的水平上发挥作用，从而实现了人工智能的“重大挑战”之一 . 我们首次开发了有效的围棋走法选择和位置评估函数，基于深度神经网络，这些网络通过监督学习和强化学习的新颖组合进行训练。 我们引入了一种新的搜索算法，该算法成功地将神经网络评估与 Monte Carlo rollouts 相结合。 我们的程序 AlphaGo 在一个高性能的树搜索引擎中大规模地将这些组件集成在一起。
• AlphaGo 与樊麾的对局，比深蓝对阵卡斯帕罗夫的棋局少了数千倍； 通过更智能地选择这些位置来补偿，使用策略网络，并使用价值网络更精确地评估它们——一种可能更接近人类游戏方式的方法。 此外，虽然深蓝依赖于手工制作的评估函数，但 AlphaGo 的神经网络是直接从游戏玩法中通过通用监督和强化学习方法直接训练的。
• 围棋在许多方面都是人工智能面临的困难的典范：具有挑战性的决策任务、难以处理的搜索空间以及如此复杂的最优解决方案，以至于使用策略或价值函数直接逼近似乎是不可行的。 之前计算机围棋的重大突破，MCTS 的引入，导致了许多其他领域的相应进步； 例如，一般游戏、经典规划、部分观察规划、调度和约束满足。 通过将树搜索与策略和价值网络相结合，AlphaGo 终于在围棋上达到了专业水平，为在其他看似棘手的人工智能领域现在可以实现人类水平的表现提供了希望。

方法

• 问题设置。许多完全信息博弈，如国际象棋、跳棋、奥赛罗、西洋双陆棋和围棋，可以定义为交替马尔可夫博弈。在这些游戏中，有一个状态空间$S$（其中状态包括当前玩家要玩的指示）；一个动作空间 $A(s)$ 定义了任何给定状态 $s\in S$ 中的合法动作；状态转换函数 $f(s,a,\xi )$定义了在状态 $s$ 中选择动作 $a$ 和随机输入 $\xi$（例如骰子）后的后继状态；最后一个奖励函数 $r^i(s)$ 描述了玩家 $i$ 在状态 $s$ 中收到的奖励。我们将注意力限制在两人零和游戏，$r^1(s)=?r^2(s)=r(s)$，具有确定性状态转换，$f(s,a,\xi )=f(s,a)$，除了在终端时间步 $T$ 之外，零奖励。 游戏的结果 $z_t=\pm r(s_T)$ 是在时间步 $t$ 时从当前玩家的角度来看游戏结束时的终端奖励。策略 $p(a|s)$ 是法律行为 $a\in A(s)$ 的概率分布。如果根据策略 $p$ 选择两个参与者的所有动作，则价值函数是预期结果，即 $v^p(s)=E[z_t|s_t=s,a_t...T～p]$ 。零和游戏有一个独特的最优价值函数 $v^{?}(s)$，它决定了两个玩家完美游戏后状态 $s$ 的结果，
  
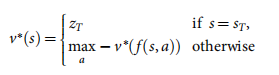
• 之前的工作。 最优值函数可以通过 minimax（或等效的 negamax）搜索递归计算。 大多数游戏对于详尽的最小 imax 树搜索来说太大了； 相反，通过使用近似值函数 $v(s)\approx v^{?}(s)$ 代替终端奖励来截断游戏。 使用 alpha-beta pruning 的深度优先极小极大搜索在国际象棋、跳棋和黑白棋中取得了超人的表现，但在围棋中效果不佳。
• 强化学习可以直接从自我博弈中学习近似最优值函数。 大多数先前的工作都集中在特征 $?(s)$ 与权重 $\theta$ 的线性组合 $v_{\theta }(s)=?(s)?\theta$。 在国际象棋、跳棋和围棋中使用时间差分学习训练权重； 或在黑白棋和拼字游戏中使用线性回归。 时差学习也被用来训练神经网络来逼近最优值函数，在西洋双陆棋中实现超人的表现； 并使用卷积网络在小板围棋中实现弱 kyu 级性能。
• 最小极大搜索的另一种方法是蒙特卡罗树搜索 (MCTS)，它通过双重近似估计内部节点的最佳值，$V^n\left(s\right)\approx v^{p^n}\left(s\right)\approx v^{?}\left(s\right)$ 。第一个近似值$V^n\left(s\right)\approx v^{p^n}\left(s\right)$ 使用 $n$ 次蒙特卡罗模拟来估计模拟策略 $P_n$ 的价值函数。第二个近似值$v^{p^n}\left(s\right)\approx v^{?}\left(s\right)$使用模拟策略 $P_n$ 代替极小极大最优动作。模拟策略根据搜索控制函数$\left(Q^n\left(s,a\right)+u\left(s,a\right)\right)$选择动作，例如 UCT，该函数选择具有更高动作值的子节点，$Q^n\left(s,a\right)=?V^n\left(f\left(s,a\right)\right)$，加上奖励 $u(s,a)$ 鼓励探索； 或者在状态 $s$ 没有搜索树的情况下，它从快速推出策略 $p_{\pi }(a|s)$中采样动作。 随着更多的模拟被执行并且搜索树变得更深，模拟策略变得越来越准确的统计数据。 在极限情况下，两个近似都变得精确并且 MCTS（例如，使用 UCT）收敛到最优值函数${\lim }_{n\to \infty }{V}^n\left(s\right)={\lim }_{n\to \infty }{v}^{p^n}\left(s\right)=v^{?}\left(s\right)$。 当前最强大的围棋程序基于 MCTS。
• MCTS 先前已与用于将搜索树的波束缩小到高概率移动的策略相结合； 或将奖金项偏向高概率移动。 MCTS 还结合了一个值函数，用于在新扩展的节点中初始化动作值，或将蒙特卡罗评估与极小极大评估相结合。 相比之下，AlphaGo 对价值函数的使用基于截断的蒙特卡罗搜索算法，该算法在游戏结束前终止推出，并使用价值函数代替终端奖励。 AlphaGo 的位置评估混合了完整的 rollout 和截断的 rollout，在某些方面类似于众所周知的时间差分学习算法 TD(λ)。 AlphaGo 还与之前的工作不同，它使用了更慢但更强大的策略和价值函数表示； 评估深度神经网络比线性表示慢几个数量级，因此必须异步发生。
• MCTS 的性能在很大程度上取决于推出策略的质量。 之前的工作重点是通过监督学习、强化学习、模拟平衡或在线适应来手工制作模式或学习推广策略； 然而，众所周知，基于 rollout 的位置评估经常不准确。 AlphaGo 使用相对简单的 rollout，而是使用价值网络更直接地解决位置评估的挑战性问题。
• 搜索算法。 为了将大型神经网络有效地集成到 AlphaGo 中，我们实施了异步策略和值 MCTS 算法 (APV-MCTS)。 搜索树中的每个节点 $s$ 包含所有合法动作 $a\in A(s)$ 的边 $(s,a)$ 。 每条边存储一组统计信息，
  
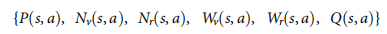
• 其中 $P(s,a)$ 是先验概率，$W_v(s,a)$和 $W_r(s,a)$ 是总动作值的蒙特卡罗估计，在 $N_v(s,a)$ 和 $N_r(s,a)$ 上累积 ) 分别是叶子评估和 rollout 奖励，$Q(s,a)$ 是该边的组合平均动作值。 多个模拟在单独的搜索线程上并行执行。 APV-MCTS 算法在图 3.
• 选择（图 3a）。 每个模拟的第一个 in-tree 阶段从搜索树的根开始，当模拟在时间步 $L$ 到达叶节点时结束。在每个时间步长 $t<L$ 中，根据搜索树中的统计数据选择一个动作，$a_t=\arg {\max }_a\left(Q\left(s_t,a\right)+u\left(s_t,a\right)\right)$ 使用 PUCT 算法的变体 p，其中 cpuct 是确定探索级别的常数； 这种搜索控制策略最初更喜欢具有高先验概率和低访问次数的动作，但渐近地喜欢具有高动作值的动作。在这些时间步中的每一个，$t<L$，根据统计选择一个动作 在搜索树 中，t 使用 PUCT 算法的变体 $u\left(s,a\right)=c_{puct}P\left(s,a\right)\frac{\sqrt{{\sum }_b{N}_r\left(s,b\right)}}{1+N_r\left(s,b\right)}$ ，其中 $c_{puct}$ 是确定探索级别的常数； 这种搜索控制策略最初更喜欢具有高先验概率和低访问次数的动作，但渐近地喜欢具有高动作值的动作。
• 评估（图 3c）。 价值网络将叶子位置 $s_L$ 添加到队列中用于评估 $v_{\theta }(s_L)$，除非它之前已经被评估过。 每个模拟的第二个推出阶段从叶节点 $s_L$ 开始，一直持续到游戏结束。 在这些时间步长中的每一个，$t\ge L$，两个玩家都根据推出策略选择动作，$a_t～p_{\pi }(?|s_t)$。 当游戏达到最终状态时，结果 $z_t=\pm r(s_T)$ 由最终得分计算得出。
• 备份（图 3d）。在模拟的每个 in-tree 步骤 $t\le L$ 处，更新 rollout 统计数据，就好像它已经输掉了 $n_{vl}$ 场比赛，$N_r(s_t,a_t)\leftarrow N_r(s_t,a_t)+n_{vl}$； $W_r(s_t,a_t)\leftarrow W_r(s_t,a_t)?n_{vl}$;这种虚拟损失阻止其他线程同时探索相同的变化。在模拟结束时，在每个步骤 $t\le L$ 的反向传递中更新 rollout 统计信息，用结果 $N_r(s_t,a_t)\leftarrow N_r(s_t,a_t)?n_{vl}+1$ 替换虚拟损失； $W_r(s_t,a_t)\leftarrow W_r(s_t,a_t)+n_{vl}+z_t$。异步地，当叶子位置 $s_L$ 的评估完成时，将启动单独的反向传递。价值网络的输出 $v_{\theta }(s_L)$ 用于在第二次反向传播中更新价值统计信息，通过每个步骤 $t\le L$, $N_v(s_t,a_t)\leftarrow N_v(s_t,a_t)+1$, $W_v(s_t,a_t)\leftarrow W_v(s_t,a_t)+v_{\theta }(s_L)$。每个状态动作的整体评估是 Monte Carlo 估计值 $\lambda$ 的加权平均值，它将价值网络和 rollout 评估与加权参数 $\lambda$ 混合在一起。所有更新都是无锁执行的。
• 扩展（图 3b）。当访问次数超过阈值 $N_r(s,a)>n_{thr}$ 时，将后继状态 $s^{\prime }=f(s,a)$ 添加到搜索树中。新节点初始化为 { N ( s ′ , a ) = N r ( s ′ , a ) = 0 , W ( s ′ , a ) = W r ( s ′ , a ) = 0 , P ( s ′ , a ) = p σ ( a ∣ s ′ ) } \{ N(s', a)=N_r(s', a)=0, W(s', a)=W_r(s', a)=0, P(s',a) =p_σ(a|s') \} {N(s′,a)=Nr?(s′,a)=0,W(s′,a)=Wr?(s′,a)=0,P(s′,a)=pσ?(a∣s′)}，使用树策略 $p_{\tau }(a|s^{\prime })$（类似于 rollout 策略，但具有更多功能，请参见扩展数据表 4）为动作选择提供占位符先验概率。位置 $s^{\prime }$ 也被插入到一个队列中，用于策略网络的异步 GPU 评估。先验概率由 SL 策略网络 ${p_{\sigma }}^{\beta }(?|s\prime )$ 计算，softmax 温度设置为 $\beta$；这些使用原子更新替换了占位符先验概率 $P( s′,a) ← {p_σ}^β(a|s′) 。阈值 $n_{thr}$ 是动态调整的，以确保将位置添加到策略队列的速率与 GPU 评估策略网络的速率相匹配。位置由策略网络和价值网络使用 mini-batch 大小为 1 来评估，以最小化端到端评估时间。
• 我们还实现了分布式 APV-MCTS 算法。 该架构由执行主搜索的单个主机、执行异步部署的多个远程工作 CPU 以及执行异步策略和价值网络评估的多个远程工作 GPU 组成。 整个搜索树存储在 master 上，它只执行每个模拟的 in-tree 阶段。 叶位置与执行模拟的推出阶段的工作 CPU 和工作 GPU 进行通信，后者计算网络特征并评估策略和价值网络。 策略网络的先验概率返回给主节点，在那里它们替换新扩展节点的占位符先验概率。 来自 rollout 的奖励和价值网络输出各自返回给 master，并备份原始搜索路径。
• 在搜索结束时，AlphaGo 选择访问次数最多的动作； 与最大化动作值相比，这对异常值不太敏感。 搜索树在后续时间步被复用：播放动作对应的子节点成为新的根节点； 这个子树下面的子树连同它的所有统计数据都被保留下来，而树的其余部分被丢弃。 AlphaGo 的比赛版本在对手的移动过程中继续搜索。 如果最大化访问次数的操作和最大化操作值的操作不一致，则扩展搜索。 时间控制被设计为在游戏中期使用大部分时间。 当 AlphaGo 的整体评估低于估计的 10% 赢得比赛的概率时，即 $ma{x}_{a}Q(s,a)<?0.8$时，AlphaGo 将辞职。
• AlphaGo 没有采用在大多数蒙特卡洛围棋程序中使用的所有棋步法或快速动作价值估计法； 当使用策略网络作为先验知识时，这些有偏见的启发式方法似乎不会带来任何额外的好处。 此外，AlphaGo 不使用渐进式加宽、动态 komi 或开局。 AlphaGo在范辉比赛中使用的参数列于扩展数据表5中。
  
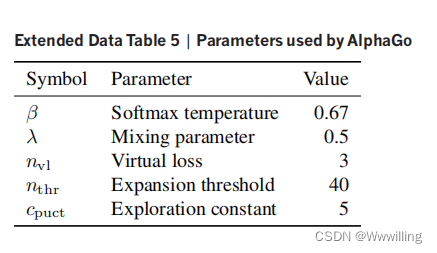
• Rollout policy。 rollout 策略$p_{\pi }(a|s)$ 是一种基于快速、增量计算、基于局部模式的特征的线性 softmax 策略，包括导致状态 $s$ 的前一个移动周围的“响应”模式和周围的“无响应”模式候选人在状态 $s$ 中移动 $a$。每个无响应模式是一个二元特征，匹配以 $a$ 为中心的特定 3×3 模式，由每个相邻交叉点的颜色（黑色、白色、空）和自由计数（1、2、≥3）定义。每个响应模式都是一个二元特征，与以前一次移动为中心的 12 点菱形模式 21 中的颜色和自由计数相匹配。此外，少量手工制作的局部特征编码常识性围棋规则（参见扩展数据表 4）。与策略网络类似，rollout 策略的权重 $\pi$ 是从 Tygem 服务器上人类游戏的 800 万个位置训练的，以通过随机梯度下降最大化对数似然。在空板上，每个 CPU 线程每秒执行大约 1,000 次模拟。
• 我们的推出策略 $p_{\pi }(a|s)$ 包含的手工知识少于最先进的围棋程序。 相反，我们利用 MCTS 中更高质量的动作选择，这是由搜索树和策略网络通知的。 我们引入了一种新技术，可以缓存搜索树中的所有移动，然后在推出期间播放类似的移动； “最后一个好的回复”启发式的概括。 在树遍历的每一步，最可能的动作都被插入到一个哈希表中，以及围绕前一个移动和当前移动的 3×3 模式上下文（颜色、自由度和石头计数）。 在 rollout 的每一步，模式上下文都会与哈希表进行匹配； 如果找到匹配，则存储的移动以高概率进行。
• 对称性。在之前的工作中，通过在卷积层中使用旋转和反射不变滤波器来利用 Go 的对称性。尽管这在小型神经网络中可能有效，但它实际上会损害大型网络的性能，因为它会阻止中间过滤器识别特定的非对称模式 。相反，我们通过使用八次反射和旋转的二面体组 $d_1(s),\dots ,d_8(s)$ 动态变换每个位置 $s$ 在运行时利用对称性。在显式对称集成中，所有 8 个位置的小批量传递到策略网络或价值网络并并行计算。对于价值网络，输出值被简单地平均 。
  
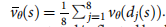
• 对于策略网络，输出概率平面被旋转/反射回原始方向，并一起平均以提供集成预测 $\sigma$ ；这种方法用于我们的原始网络评估（参见扩展数据表 3）。相反，APV-MCTS 使用隐式对称集成，为每个评估随机选择单个旋转/反射$j\in [1,8]$。我们只计算该方向的一个评估；在每次模拟中，我们通过 $v_{\theta }(d_j(s_L))$ 计算叶节点 $s_L$ 的值，并允许搜索过程对这些评估进行平均。类似地，我们为单个随机选择的旋转/反射计算策略网络
  
• 策略网络：分类。我们训练策略网络 $p_{\sigma }$ 以根据 KGS 数据集中的专家动作对位置进行分类。该数据集包含 KGS 6 至 9 位人类玩家玩的 160,000 场比赛中的 2940 万个位置； 35.4% 的游戏是差点游戏。数据集分为测试集（前一百万个位置）和训练集（其余 2840 万个位置）。传球动作被排除在数据集中。每个位置都由原始棋盘描述 $s$ 和人类选择的移动 $a$ 组成。我们扩充了数据集以包括每个位置的所有八个反射和旋转。为每个位置预先计算了对称增强和输入特征。对于每个训练步骤，我们从增强的 KGS 数据集中随机选择了 $m$ 个小批量样本，${\left\{s^k,a^k\right\}}_{k=1}^m$并应用异步随机梯度下降更新以最大化动作的对数似然，$\Delta \sigma =\frac{a}{m}{\sum }_{k=1}^m\frac{?\log p_{\sigma }\left(a^k|s^k\right)}{?\sigma }$。步长 $\alpha$ 初始化为 0.003，每 8000 万个训练步减半，没有动量项，小批量大小为 $m=16$。使用 DistBelief 在 50 个 GPU 上异步应用更新；超过 100 步的梯度被丢弃。 3.4 亿个训练步骤需要大约 3 周的时间。
• 策略网络：强化学习。我们通过策略梯度强化学习进一步训练了策略网络。每次迭代都包含并行运行的小批量 $n$ 个游戏，在当前正在训练的策略网络 $p_{\rho }$ 和使用来自先前迭代的参数 ${\rho }^{?}$的对手 ${p_{\rho }}^{?}$之间，从池中随机采样以增加训练的稳定性。权重被初始化为 $\rho ={\rho }^{?}=\sigma$。每 500 次迭代，我们将当前参数 $\rho$ 添加到对手池中。小批量中的每个游戏 $i$ 一直进行到步骤 $T_i$ 终止，然后从每个玩家的角度进行评分以确定结果 $z_t^i=\pm r\left(s_{T^i}\right)$。然后重播游戏以确定策略梯度更新，$\Delta \rho =\frac{a}{n}{\sum }_{i=1}^n{\sum }_{t=1}^{T^i}\frac{?\log p_{\rho }\left(a_t^i|{s_t}^i\right)}{?\rho }\left(z_t^i?v\left(s_t^i\right)\right)$，使用 REINFORCE 算法 与基线$v\left(s_t^i\right)$用于方差减少。在第一次通过训练管道时，基线设置为零；在第二遍中，我们使用价值网络 $v_{\theta }(s)$ 作为基线；这提供了一个小的性能提升。以这种方式对策略网络进行了一天的训练，使用 50 个 GPU，对 128 个游戏的 10,000 个小批量进行训练。
• 价值网络：回归。我们训练了一个价值网络 $v_{\theta }(s)\approx v^{p_{\rho }}(s)$来近似 RL 策略网络 $p_{\rho }$ 的价值函数。为了避免过度拟合游戏中强相关的位置，我们构建了一个与不相关的自我游戏位置的新数据集。这个数据集包含超过 3000 万个位置，每个位置都来自一个独特的自我游戏。每个游戏都是通过随机采样时间步长 U ～ u n i f { 1 , 450 } U \sim unif \{1, 450 \} U～unif{1,450} 以及从 SL 策略网络中采样前 $t=1,\dots U?1$ 移动，$a_t～p_{\sigma }(?|s_t)$ 来分三个阶段生成的；然后从可用的移动中随机均匀地采样一个移动， a U ～ u n i f { 1 , 361 } a_U \sim unif \{1, 361 \} aU?～unif{1,361}（重复直到 $a_U$ 合法）；然后从 RL 策略网络 $a_t～p_{\rho }(?|s_t)$ 对剩余的移动序列进行采样，直到游戏结束，$t=U+1,\dots T$。最后，对游戏进行评分以确定结果 $z_t=\pm r(s_T)$。每个游戏的数据集中只添加了一个训练示例 $(s_{U+1},z_{U+1})$。该数据提供了价值函数的无偏样本。
  
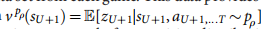
• 在生成的前两个阶段，我们从噪声较大的分布中进行采样，以增加数据集的多样性。训练方法与 SL 策略网络训练相同，不同之处在于参数更新基于预测值和观察到的奖励之间的均方误差，
  
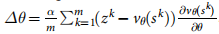
• 价值网络使用 50 个 GPU 对 32 个位置的 5000 万个小批量进行了为期一周的训练。
• 策略/价值网络的功能。每个位置 $s$ 被预处理成一组 19×19 的特征平面。我们使用的特征直接来自游戏规则的原始表示，表明围棋棋盘的每个交叉点的状态：棋子颜色、自由度（棋子链的相邻空点）、捕获、合法性、自下棋以来的回合数，和（仅适用于价值网络）当前要播放的颜色。此外，我们使用一个简单的战术特征来计算阶梯搜索的结果。所有特征都是相对于当前要播放的颜色计算的；例如，每个交叉点的石头颜色表示为玩家或对手，而不是黑色或白色。每个整数特征值被分成多个 19×19 平面的二进制值（one-hot encoding）。例如，单独的二元特征平面用于表示交叉点是否具有 1 个liberties自由、2 个自由、……、≥8 个自由。完整的特征平面集列在扩展数据表 2 中。
  
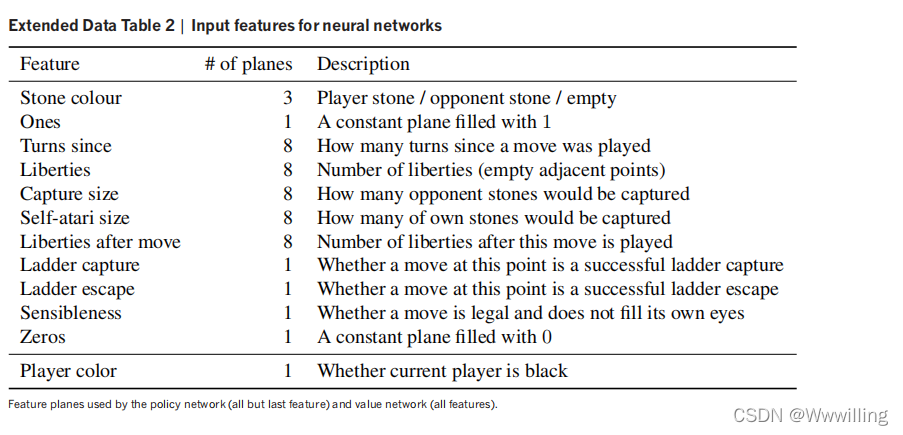
• 神经网络架构。 策略网络的输入是由 48 个特征平面组成的 19×19×48 图像堆栈。 第一个隐藏层零将输入填充为 23×23 的图像，然后将 $k$ 个内核大小为 5×5 的滤波器与输入图像进行卷积，步幅为 1，并应用整流器非线性。 随后的隐藏层 2 到 12 中的每一个都将各自的前一个隐藏层零填充到一个 21×21 的图像中，然后将$k$ 个内核大小为 3×3 的滤波器与步长 1 进行卷积，再次跟随非线性整流器。 最后一层将内核大小为 1×1 的 1 个滤波器与步长 1 进行卷积，每个位置具有不同的偏差，并应用 softmax 函数。 AlphaGo 的比赛版本使用了 $k=192$ 个过滤器； 图 2b 和扩展数据表 3 还显示了使用 k = 128、256 和 384 个滤波器的训练结果。
• 价值网络的输入也是一个 19×19×48 的图像堆栈，还有一个额外的二元特征平面描述当前要播放的颜色。 隐藏层 2 到 11 与策略网络相同，隐藏层 12 是一个额外的卷积层，隐藏层 13 卷积 1 个内核大小为 1×1 的滤波器，步幅为 1，隐藏层14是一个全连接的线性层，有256个整流单元。 输出层是具有单个 tanh 单元的全连接线性层。
• 评估。我们通过举办内部锦标赛并测量每个程序的 Elo 等级来评估计算机围棋程序的相对强度。我们通过逻辑函数
  
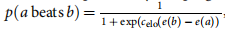
• 估计程序 a 击败程序 b 的概率，并通过 BayesElo 程序使用标准常数 $c_{elo}=1/400$ 计算的贝叶斯逻辑回归估计评分 $e(?)$。该量表基于职业围棋选手范慧的 BayesElo 评分（提交日期为 2,908）。所有程序每次移动最多接收 5 秒的计算时间；比赛使用中国规则计分，科米为 7.5 分（加分以补偿白棋第二名）。我们还玩了让 AlphaGo 与现有围棋程序下白棋的让分游戏；对于这些游戏，我们使用了非标准的让分系统，其中保留了科米，但在通常的让分点上给了黑色额外的石头。使用这些规则，$K$ 个棋子的让分点相当于给黑棋 $K?1$ 步自由步，而不是使用标准的无 Komi 让点规则的 $K?1/2$ 个自由步。我们使用这些让分规则是因为 AlphaGo 的价值网络专门训练为使用 7.5 的 komi。
• 除了分布式 AlphaGo 之外，每个计算机围棋程序都在自己的单机上执行，具有相同的规格，使用最新的可用版本和该程序支持的最佳硬件配置（参见扩展数据表 6）。 在图 4 中，计算机程序的近似排名基于该程序达到的最高 KGS 排名； 但是，KGS 版本可能与公开版本不同。
• 对范辉的比赛由公正的裁判进行仲裁。 5 场正式比赛和 5 场非正式比赛以 7.5 komi、无让分上限和中国规则进行。 AlphaGo 分别以 5-0 和 3-2 赢得了这些游戏（图 6 和扩展数据表 1）。 正式比赛的时间控制是 1 小时的主要时间加上三个 30 秒的比赛时间。 非正式游戏的时间控制是三个 30 秒 byoyomi。 赛前范辉选择了时间控制和比赛条件； 还同意整体比赛结果将完全由正式比赛决定。 为了大致评估范慧对计算机围棋程序的相对评级，我们将所有十场比赛的结果附加到我们的内部比赛结果中，忽略了时间控制的差异。