B样条曲线产生背景
1. Bezier曲线的不足:
- 给定
n
+
1
n+1
n+1 个控制点,则曲线的阶数
n
n
n 确定
顶点数很多时,多项式阶数大,导数阶数大,曲线有很多极值点(导数为0的点),曲线产生振荡现象。 - 使用低阶的Bezier曲线拼接较复杂(需要满足一定的连续性)
- Bezier曲线不能做局部修改
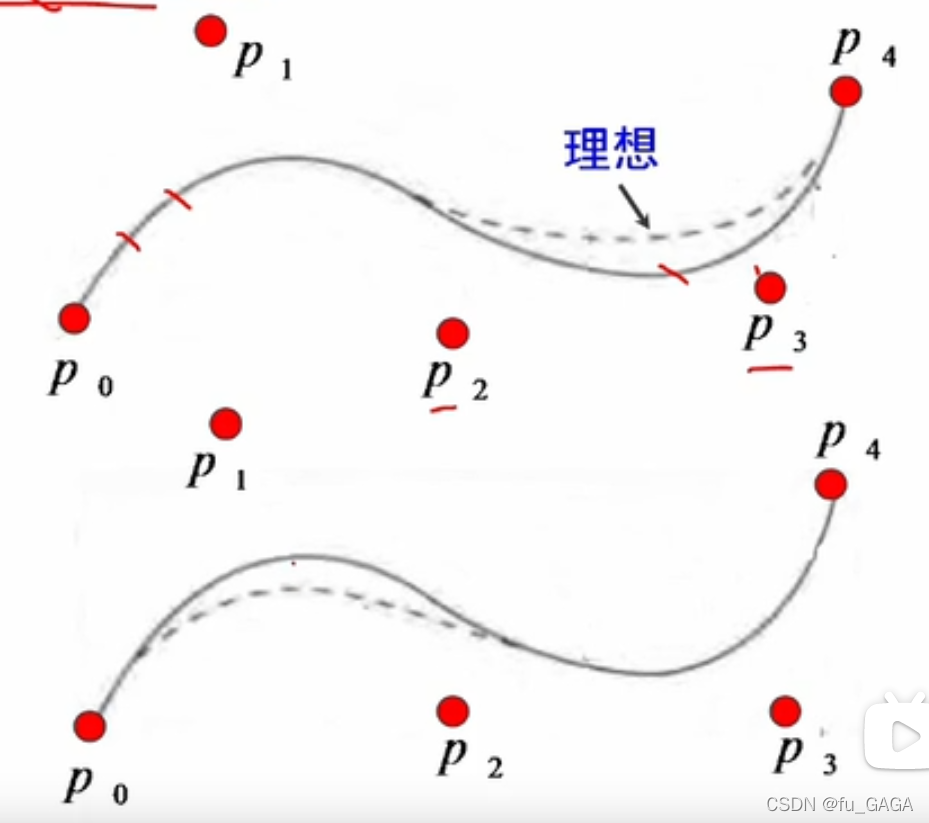
“牵一发而动全身”:修改单个控制点,会改变整条曲线的形状
【原因分析】
B
e
r
n
s
t
e
i
n
Bernstein
Bernstein多项式
B
j
n
(
t
)
B^n_j(t)
Bjn?(t) 对称,并且满足在
t
∈
(
0
,
1
)
t∈(0,1)
t∈(0,1) 时均不为0
(函数值不为0的区间通常叫做该函数的支撑区间)
对称性如下图所示:
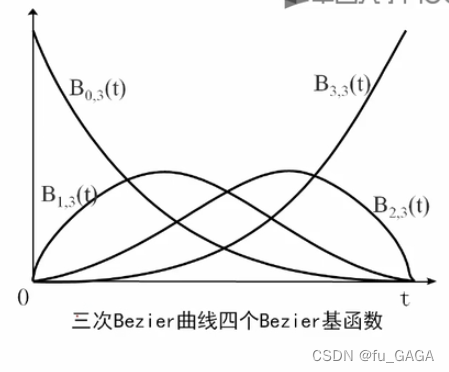
Bezier曲线:
b n ( t ) = ∑ j n b j ? B j n ( t ) b_n(t)=\sum_{j}^{n}b_j*B^n_j(t) bn?(t)=∑jn?bj??Bjn?(t)
相当于
B
e
r
n
s
t
e
i
n
Bernstein
Bernstein多项式对控制点
b
j
b_j
bj? 的加权和
由于
B
j
n
(
t
)
≠
0
B^n_j(t)≠0
Bjn?(t)?=0 (在整个区间
[
0
,
1
]
[0,1]
[0,1] 上有支撑),所以每个控制点的改变都会影响整条Bezier曲线
2.B样条曲线的引入
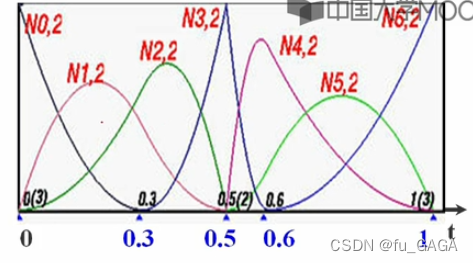
图中7个混合函数
N
i
,
2
N_{i,2}
Ni,2?
(
i
=
0
,
1
,
2...6
)
(i=0,1,2...6)
(i=0,1,2...6)
每个混合函数的支撑区间只是
[
0
,
1
]
[0,1]
[0,1] 的一部分,例:
- N 1 , 2 N_{1,2} N1,2? 的支撑区间是 [ 0 , 0.5 ] [0,0.5] [0,0.5]
- N 2 , 2 N_{2,2} N2,2? 的支撑区间是 [ 0 , 0.5 ] [0,0.5] [0,0.5]
- N 4 , 2 N_{4,2} N4,2?的支撑区间是 [ 0.5 , 1 ] [0.5,1] [0.5,1]
B样条曲线提出:保留全部Bezier曲线优点的同时,克服了其缺点
(样条spline:分段连续多项式!)
整条曲线用一个完整的表达形式(但内在的量是低阶一段一段的)
【Example:三次样条】
现有
n
+
1
n+1
n+1 个点,每两个点之间构造一个多项式,则有
n
n
n 个小区间
- 每个小区间构造一个三次多项式
- n段三次多项式拼接在一起
- 段与段之间要两次连续
- 采用Bezier曲线:5个点,则构造出4次多项式
- 采用三次样条:5个点,四段三次多项式,段间两次连续
3. B样条定义 vs Bezier曲线定义
B样条曲线数学表达式:
P
(
u
)
=
∑
j
=
0
n
P
i
?
B
i
,
k
(
u
)
P(u)=\sum_{j=0}^nP_i*B_{i,k}(u)
P(u)=∑j=0n?Pi??Bi,k?(u)
(
u
∈
[
u
k
?
1
,
u
n
+
1
]
)
(u∈[u_{k-1},u_{n+1}])
(u∈[uk?1?,un+1?])
Bezier曲线数学表达式:
P
(
u
)
=
∑
j
=
0
n
P
i
?
B
i
,
n
(
u
)
P(u)=\sum_{j=0}^nP_i*B_{i,n}(u)
P(u)=∑j=0n?Pi??Bi,n?(u)
(
u
∈
[
0
,
1
]
)
(u∈[0,1])
(u∈[0,1])
不同之处:
(1)B样条基函数与控制点个数 n + 1 n+1 n+1(或阶数 n n n)无关
- B i , k ( u ) B_{i,k}(u) Bi,k?(u) : k k k 阶( k ? 1 k-1 k?1 次)B样条基函数 k ∈ [ 2 , n + 1 ] k∈[2,n+1] k∈[2,n+1]
(2)两者参数 u u u的取值范围不同:
-
u
∈
[
u
k
?
1
,
u
n
+
1
]
u∈[u_{k-1},u_{n+1}]
u∈[uk?1?,un+1?]

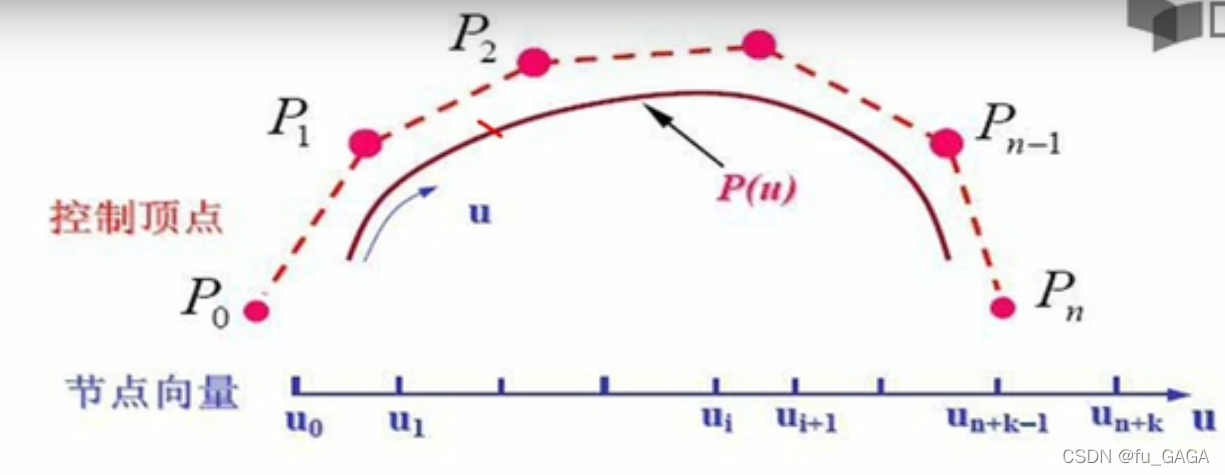
4. B样条基函数定义 —— de Boor-Cox递推定义
【idea】
构造一种递推公式,由0次构造1次,1次构造2次,2次构造3次…最终构造出k阶(k-1次)的B样条基函数
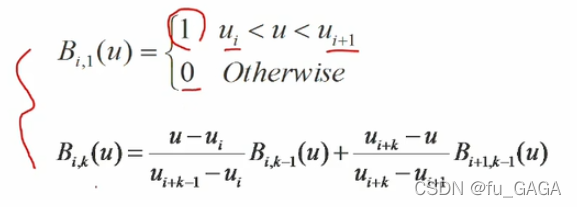
并且约定
0
/
0
=
0
0/0=0
0/0=0
k阶的B样条基函数由两个k-1阶的B样条基函数线性组合而成
要确定第
i
i
i 个
k
k
k 阶B样条
B
i
,
k
(
u
)
B_{i,k}(u)
Bi,k?(u) :
要用到
u
i
,
u
i
+
1
,
.
.
.
,
u
i
+
k
u_i,u_{i+1},...,u_{i+k}
ui?,ui+1?,...,ui+k? 共
k
+
1
k+1
k+1 个节点
↓
[
u
i
,
u
i
+
k
]
[u_i,u_{i+k}]
[ui?,ui+k?] 称为
B
i
,
k
(
u
)
B_{i,k}(u)
Bi,k?(u) 的支撑区间
【推导举例】
1阶0次B样条:
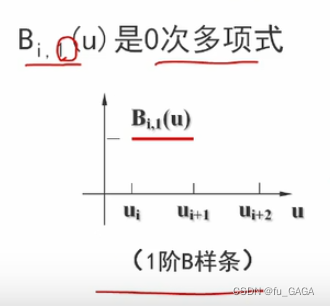
2阶1次B样条:
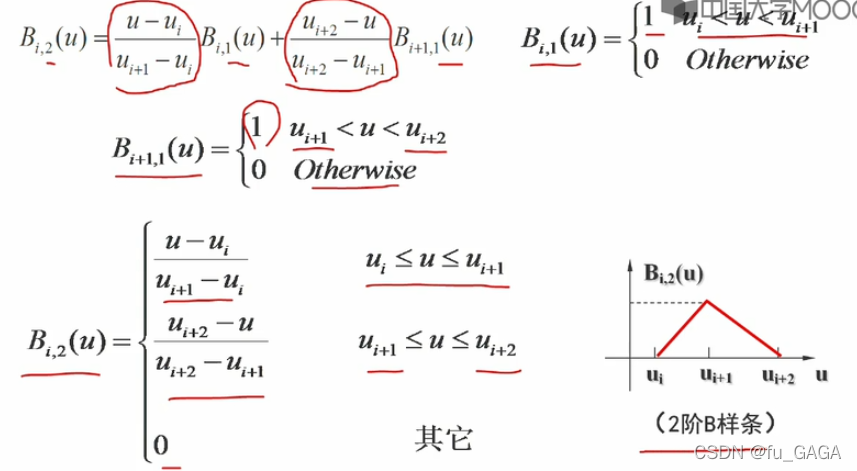
3阶2次B样条:
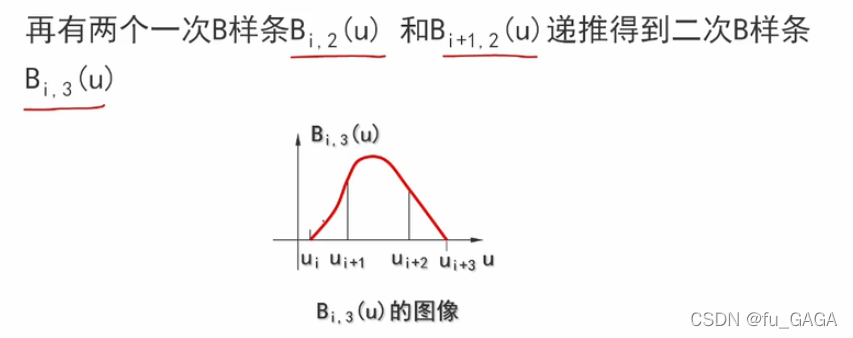
【问题Question】
No.1:对 n + 1 n+1 n+1 个顶点, k k k 阶B样条曲线需要多少个节点向量 u i u_i ui? 与之匹配?
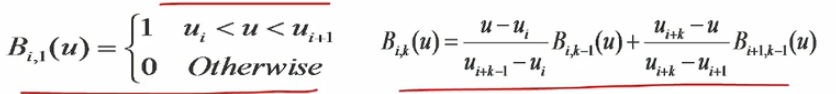
- B i , 1 B_{i,1} Bi,1? 1阶0次基函数:涉及1个区间 [ u i , u i + 1 ] [u_i,u_{i+1}] [ui?,ui+1?],2个节点
- B i , 2 B_{i,2} Bi,2?(由 B i , 1 , B i + 1 , 1 B_{i,1},B_{i+1,1} Bi,1?,Bi+1,1?组成):2个区间 [ u i , u i + 1 ] , [ u i + 1 , u i + 2 ] [u_i,u_{i+1}],[u_{i+1},u_{i+2}] [ui?,ui+1?],[ui+1?,ui+2?],3个节点
- B i , 3 B_{i,3} Bi,3?(由 B i , 2 , B i + 1 , 2 B_{i,2},B_{i+1,2} Bi,2?,Bi+1,2?组成):3个区间,4个节点
- B i , k B_{i,k} Bi,k?(由 B i , 2 , B i + 1 , 2 B_{i,2},B_{i+1,2} Bi,2?,Bi+1,2?组成):k个区间,k+1个节点
当 i = n i=n i=n 时,第n段多项式,需要n+k+1个节点向量与之匹配
节点向量个数 n + k + 1 n+k+1 n+k+1 = 阶数 k k k + 顶点数 n + 1 n+1 n+1
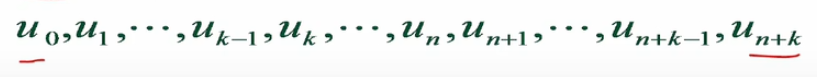
No.2 :每个 p i p_i pi? 都有一个 B i , k ( u ) B_{i,k}(u) Bi,k?(u) 与之匹配,曲线的次数是 k ? 1 k-1 k?1 次,这条曲线的定义区间是什么?(Bezier曲线的定义区间是 [ 0 , 1 ] [0,1] [0,1])
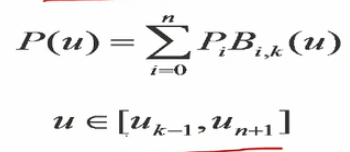

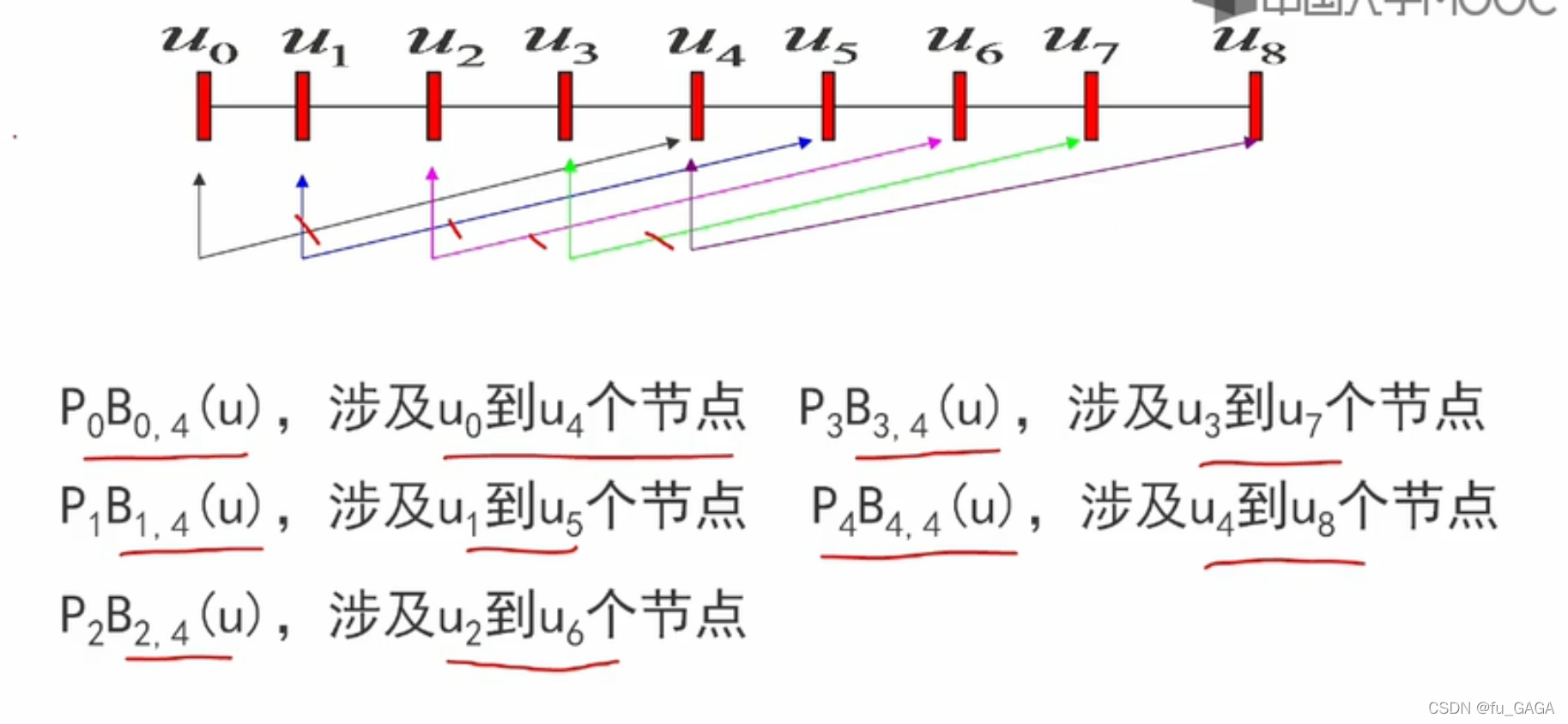
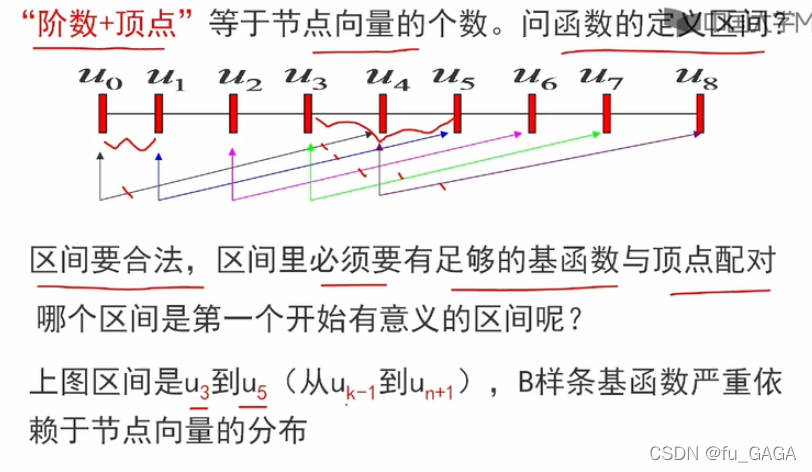
函数定义区间合法 → 所有与顶点配对的基函数在该区间内都有定义(都覆盖)
- u k ? 1 u_{k-1} uk?1? 是第一个基函数 B 0 , k B_{0,k} B0,k? 的结束节点前一个节点
- u n + 1 u_{n+1} un+1? 是最后一个基函数 B n , k B_{n,k} Bn,k? 的开始节点后一个节点
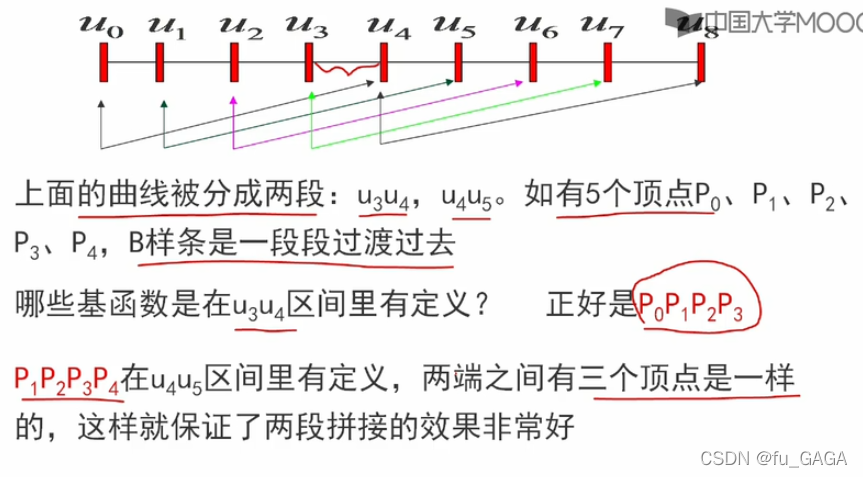
5. 总结
