核心思想
??本文提出一种6D位姿跟踪算法,能够在没有目标实例3D模型或同类型物体的3D模型的条件下,实现目标物体位姿的准确估计和跟踪。相对于依赖3D模型的位姿估计和跟踪算法,本文提出的方法只需要输入一个RGB-D图像序列,以及在第一幅图像 I 0 I_0 I0?上目标物体的分割图 M 0 M_0 M0?,就能实现目标物体位姿的实时跟踪。如果需要目标物体相对于相机的位姿,还需要给定目标物体在第一帧图像中相对于相机的位姿 T 0 C T_0^C T0C?。也就是说本文给出的是当前帧中目标物体相对于第一帧中目标物体的位姿变化 T 0 → τ T_{0\rightarrow\tau} T0→τ?,而目标物体相对于相机的位姿 T τ = T 0 → τ T 0 C T_{\tau}=T_{0\rightarrow\tau} T_0^C Tτ?=T0→τ?T0C?。作者首先利用视频目标分割算法transductive-VOS将目标物体从图像序列中分割出来,然后利用LF-Net算法提取相邻帧的关键点特征并匹配,采用RANSAC算法去除误匹配点,利用最小二乘法方法计算相邻帧之间的位姿变换 T t t ? 1 T_t^{t-1} Ttt?1?,然后得到当前帧目标位姿的初步估计结果 T ~ t \tilde{T}_t T~t?。从一系列图像序列中提取出关键帧,并将关键帧中的目标物体位姿作为节点,构成目标位姿图(Object Pose Graph),利用在线图优化的方法改进当前帧位姿初步估计的结果,得到当前的最终位姿 T t T_t Tt?。
实现过程
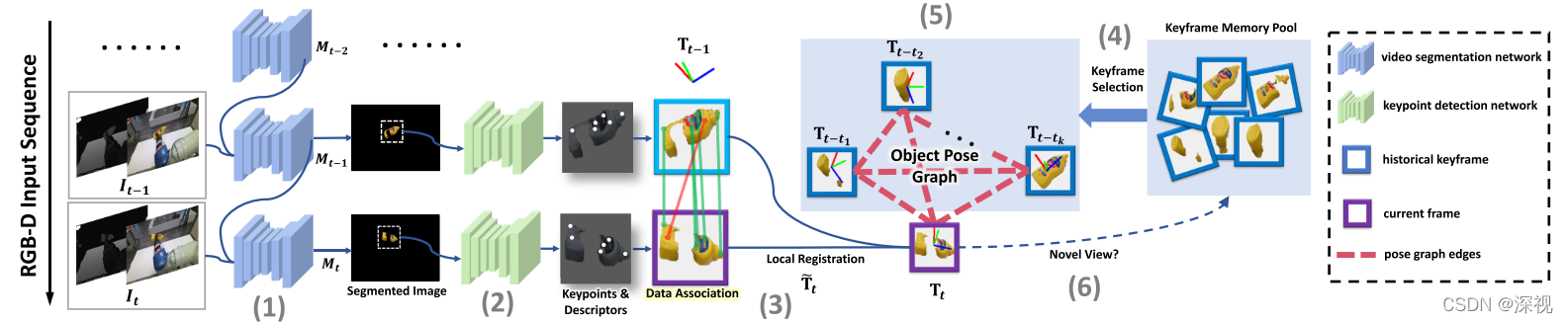
??首先,根据第一帧图像中目标物体的分割结果
M
0
M_0
M0?,利用transductive-VOS算法实现整个图像序列的目标物体分割。相对于Mask-RCNN等对于图像进行语义分割的算法,transductive-VOS充分利用图像序列之间连续性和相似性,将前一帧图像的分割结果传播到当前帧的图像中,提高了图像分割的效率。而且本文的方法只需要得到目标物体的二元分割掩码
M
τ
M_{\tau}
Mτ?,不要实现语义或实例分割,因此也可以采用其他的图像分割方法。
??然后,利用相邻帧之间局部配准方法来初步估计目标物体的位姿
T
~
t
\tilde{T}_t
T~t?。采用基于深度学习的关键点提取算法LF-Net从相邻帧的图像中分别提取关键点及相应的特征向量,并利用RANSAC算法进行关键点特征匹配并筛除误匹配点。每三对匹配点构成一个配准样本,采用最小二乘法计算相邻帧之间的位姿变换
T
t
t
?
1
T_t^{t-1}
Ttt?1?,进而根据前一帧的目标位姿估计结果
T
t
?
1
T_{t-1}
Tt?1?,得到当前帧的位姿初步估计结果
T
~
t
=
T
t
?
1
T
t
t
?
1
\tilde{T}_t=T_{t-1}T_t^{t-1}
T~t?=Tt?1?Ttt?1?。
??接下来,从关键帧记忆池
N
\mathcal{N}
N中提取
K
\mathcal{K}
K幅关键帧图像用于优化位姿初步估计结果。目标是寻找到与当前帧拥有最大共有视野重叠的关键帧,来充分利用多视角间的连续性。这可以看作是从一个加权边有向图中寻找最小化H-subgraph的问题:
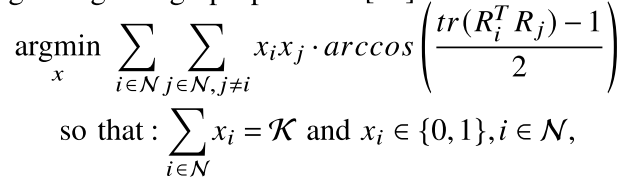
其中
R
i
R_i
Ri?表示对应关键帧的旋转矩阵。利用旋转矩阵之间的测地距离(geodesic distance)来描述旋转矩阵之间的差异,当两幅图像相对于相机的旋转矩阵之间的差异最小时,则说明两幅图像之间的共有视野重叠部分达到最大。而通过组合优化算法求解上式,算法的复杂度较高。本文采用一种迭代的贪婪选择算法,以第一帧图像
I
0
I_0
I0?作为初始帧构建一个关键帧集合
K
\mathcal{K}
K。
??最后,使用目标位姿图优化算法,利用提取的关键帧集合对初步位姿估计结果进行优化。位姿图
G
=
{
V
,
E
}
G=\{V,E\}
G={V,E},共有
k
+
1
k+1
k+1个节点,节点表示当前帧以及对应
k
k
k个关键帧的目标位姿。节点之间的边包含两种权重:
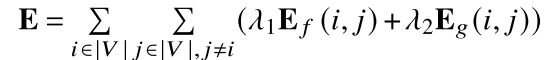
其中
E
f
E_f
Ef?表示特征匹配点之间的差异:
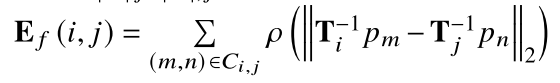
C
i
,
j
C_{i,j}
Ci,j?是关键点提取和匹配过程中得到的匹配点之间的对应关系,
p
p
p表示相机坐标系下未投影的3D点,
ρ
\rho
ρ是采用Huber损失的M-estimator。
E
g
E_g
Eg?通过稠密的像素点到平面的距离来计算几何差异:
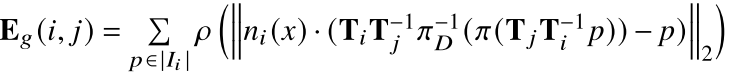
π
(
?
)
\pi(\cdot)
π(?)表示透视投影过程,
π
(
?
)
D
?
1
\pi(\cdot)^{-1}_D
π(?)D?1?表示逆透视投影过程,根据像素点的深度信息
D
D
D恢复3D点在相机坐标系下的坐标,
n
i
(
?
)
n_i(\cdot)
ni?(?)表示像素点在图像
I
i
I_i
Ii?中的法向量。构建上述位姿图的目标是寻找最优的位姿
ξ
?
\xi^*
ξ?:
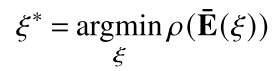
E
ˉ
(
ξ
)
\bar{E}(\xi)
Eˉ(ξ)表示堆叠的权重差异向量,
ξ
\xi
ξ表示
k
+
1
k+1
k+1个位姿向量,
ξ
i
=
l
o
g
(
T
i
)
\xi_i=log(T_i)
ξi?=log(Ti?)是在李代数下的参数化形式,包含三个平移参数和三个旋转参数。求解上式的方法,是将
ξ
\xi
ξ进行一阶泰勒展开,然后通过高斯-牛顿法以迭代的方式来解决非线性最小二乘法问题:
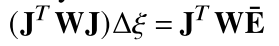
J
J
J表示
ξ
\xi
ξ的雅可比矩阵,
W
W
W表示由
ρ
\rho
ρ计算得到的对角化权重矩阵,在每次迭代过程中都会更新权重。经过反复迭代得到图中每个节点对应的位姿估计结果
T
i
=
e
x
p
(
ξ
i
)
T_i=exp(\xi_i)
Ti?=exp(ξi?)。
??本文的位姿跟踪效果与其他算法的比较如下图所示

创新点
- 提出了一种无需3D模型的,只需要RGB-D图像和目标分割图像就能实现目标位姿跟踪的算法
- 利用位姿图优化的方法,根据关键帧图像之间的连续性来改进位姿估计的结果
- 利用CUDA将算法进行并行化处理,提高了计算的效率
算法评价
??本文的贡献体现在使用一种无模型的位姿跟踪算法却达到了有模型算法的精度,仅需要RGB-D相机和目标物体的分割图就能实现目标物体位姿的准确跟踪,这在非常多的领域中还是有很高的应用价值的。但本文主要侧重的是位姿跟踪,也就是估计两帧图像之间的位姿变换,而无法直接得到目标物体的绝对位姿,需要根据给定的第一帧图像中目标物体的位姿来计算。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。