本系列博客包括6个专栏,分别为:《自动驾驶技术概览》、《自动驾驶汽车平台技术基础》、《自动驾驶汽车定位技术》、《自动驾驶汽车环境感知》、《自动驾驶汽车决策与控制》、《自动驾驶系统设计及应用》,笔者不是自动驾驶领域的专家,只是一个在探索自动驾驶路上的小白,此系列丛书尚未阅读完,也是边阅读边总结边思考,欢迎各位小伙伴,各位大牛们在评论区给出建议,帮笔者这个小白挑出错误,谢谢!
此专栏是关于《自动驾驶汽车环境感知》书籍的笔记
2.深度前馈网络
2.1 神经元
-
人工神经元(artificial neuron)简称神经元(neuron),是构成神经网络的基本单元,主要是模拟生物神经元的结构和特性,接收一组输入信号并产出输出;
-
神经元模型:
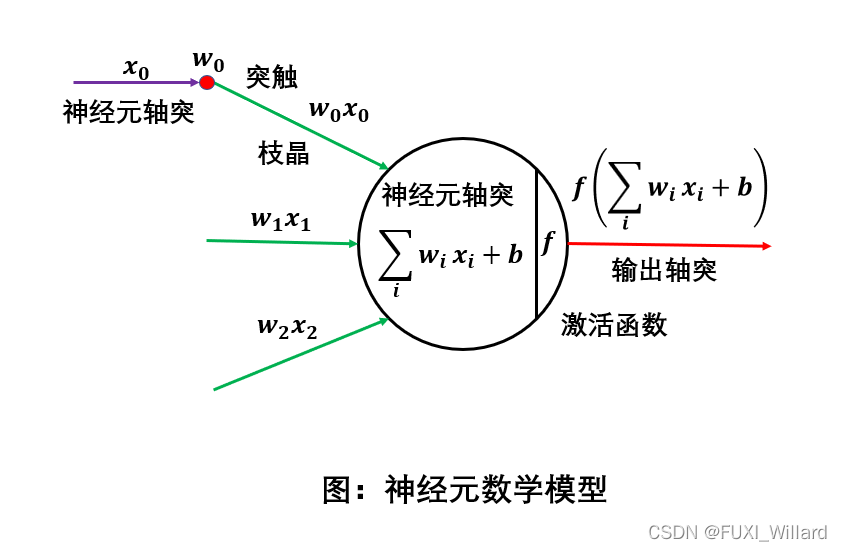
f ( ∑ i ω i x i + b ) f(\sum_i\omega_ix_i+b) f(i∑?ωi?xi?+b)
其中: f f f为激活函数;为了增强网络的表达能力及学习能力,一般使用连续非线性激活函数(activation function);- sigmoid激活函数
sigmoid激活函数的两种形式:logistic函数和tanh函数;
logistic函数定义为: σ ( x ) \sigma(x) σ(x):
σ ( x ) = 1 1 + e ? x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e?x1?
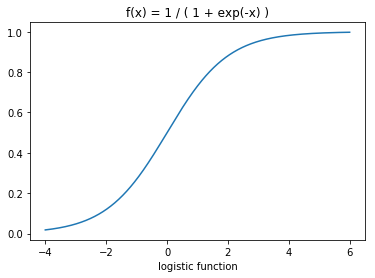
logistic函数图像如上,可以看成一个"挤压"函数,把一个实数域的输入"挤压"到(0,1);当输入值在0附近时,sigmoid函数近似线性函数;当输入值靠近两端时,对输入进行抑制;输入越小,其值越接近0;输入越大,其值越接近1;
tanh函数定义为tanh(x):
t a n h ( x ) = e x ? e ? x e x + e ? x = 2 σ ( 2 x ) ? 1 tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2\sigma(2x)-1 tanh(x)=ex+e?xex?e?x?=2σ(2x)?1
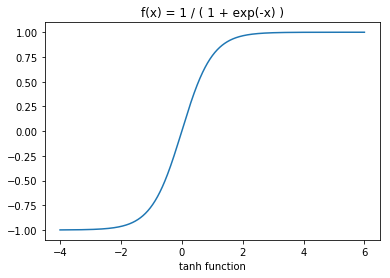
- Hard-Logistic和Hard-tanh函数
logistic函数的导数为: σ ′ ( x ) = σ ( x ) ( 1 ? σ ( x ) ) \sigma'(x)=\sigma(x)(1-\sigma(x)) σ′(x)=σ(x)(1?σ(x));logistic函数在0附近的一阶泰勒展开式为:
g l ( x ) ≈ σ ( 0 ) + x × σ ′ ( 0 ) = 0.25 x + 0.5 gl(x)≈\sigma(0)+x\times\sigma'(0)=0.25x+0.5 gl(x)≈σ(0)+x×σ′(0)=0.25x+0.5
h a r d ? l o g i s t i c ( x ) = { 1 g l ( x ) ≥ 1 g l ( x ) 0 < g l ( x ) < 1 = max ? ( min ? ( g l ( x ) , 1 ) , 0 ) 0 g l ( x ) ≤ 0 hard-logistic(x)= \left\{ \begin{array}{lr} 1& & gl(x) \ge 1\\ gl(x) && 0 < gl(x)<1=\max(\min(gl(x),1),0)\\ 0 & &gl(x)≤0 \end{array} \right. hard?logistic(x)=????1gl(x)0??gl(x)≥10<gl(x)<1=max(min(gl(x),1),0)gl(x)≤0?
tanh函数在0附近的一阶泰勒展开式为:
g t ( x ) ≈ tanh ? ( 0 ) + x × tanh ? ′ ( 0 ) x gt(x)≈\tanh(0)+x\times\tanh'(0)x gt(x)≈tanh(0)+x×tanh′(0)x
则
h a r d ? t a n h ( x ) = max ? ( min ? ( g t ( x ) , 1 ) , ? 1 ) = max ? ( min ? ( x , 1 ) , ? 1 ) hard-tanh(x)=\max(\min(gt(x),1),-1)=\max(\min(x,1),-1) hard?tanh(x)=max(min(gt(x),1),?1)=max(min(x,1),?1)
3.修正线性单元
修正线性单元(Rectified Linear Unit,ReLU),ReLU函数实际是一个斜坡函数,定义:
r e c t i f i e r ( x ) = { x x ≥ 0 0 x < 0 = max ? ( 0 , x ) rectifier(x)= \left\{ \begin{array}{lr} x& & x \ge 0\\ 0 && x<0 \end{array} \right.=\max(0,x) rectifier(x)={x0??x≥0x<0?=max(0,x)
注:rectifier函数为左饱和函数,在 x > 0 x>0 x>0时导数为1,在 x ≤ 0 x≤0 x≤0时导数为0;在训练时,学习率设置过大,在一次更新参数后,一个采用ReLU的神经元在所有的训练数据上都不能被激活;- 带泄露的ReLU
带泄露的ReLU(Leaky ReLU)在输入 x < 0 x<0 x<0时,保持一个很小的梯度;这样当神经元非激活时也有一个非零的梯度可以更新参数,避免永远不能被激活,定义:
f ( x ) = max ? ( 0 , x ) + γ min ? ( 0 , x ) = { x x ≥ 0 γ x x < 0 ; γ ∈ ( 0 , 1 ) 是 一 个 很 小 的 常 数 , 如 0.01 f(x)=\max(0,x)+\gamma\min(0,x)=\left\{ \begin{array}{lr} x& & x \ge 0\\ \gamma{x} && x<0 \end{array} \right.;\gamma\in(0,1)是一个很小的常数,如0.01 f(x)=max(0,x)+γmin(0,x)={xγx??x≥0x<0?;γ∈(0,1)是一个很小的常数,如0.01 - 带参数的ReLU
带参数的ReLU(Parametric ReLU,PReLU)引入一个可学习的参数,不同神经元可以有不同的参数;对于第 i i i个神经元,ReLU定义:
P R e L U i ( x ) = max ? ( 0 , x ) + γ i min ? ( 0 , x ) = { x x > 0 γ i x x ≤ 0 ; γ i 为 x ≤ 0 时 函 数 的 斜 率 PReLU_i(x)=\max(0,x)+\gamma_i\min(0,x)=\left\{ \begin{array}{lr} x& & x > 0\\ \gamma_i{x} && x≤0 \end{array} \right.;\gamma_i为x≤0时函数的斜率 PReLUi?(x)=max(0,x)+γi?min(0,x)={xγi?x??x>0x≤0?;γi?为x≤0时函数的斜率 - softplus函数
softplus函数定义:
s o f t p l u s ( x ) = log ? ( 1 + e x ) softplus(x)=\log(1+e^x) softplus(x)=log(1+ex)
- sigmoid激活函数
2.2 网络结构
常用的神经网络结构:
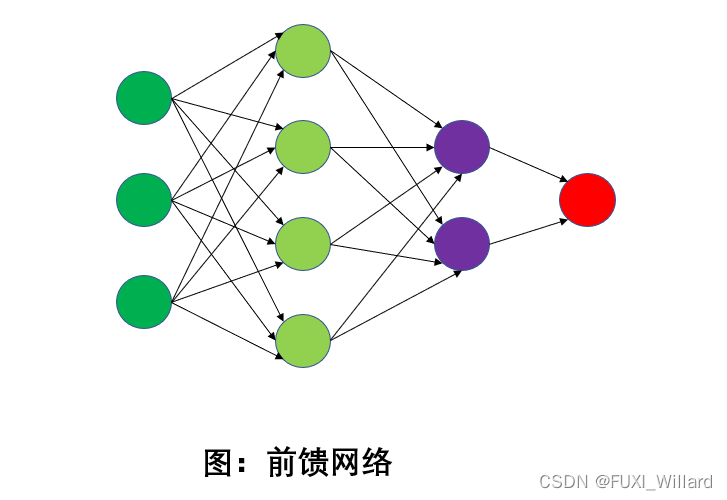
- 前馈网络;
- 网络中各个神经元按接收信息的先后分为不同的组;每一个组可以看成一个神经层;
- 每一层的神经元接收前一层神经元的输出,并输出到下一层神经元;
- 整个网络中信息只朝一个方向传播,没有反向的信息传播;
- 前馈网络包括:全连接前馈网络和卷积神经网络;
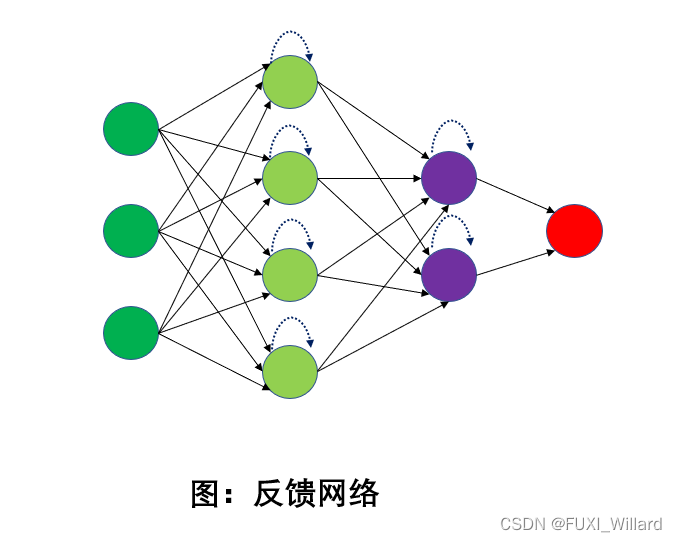
- 反馈网络;
- 网络中神经元可以接收其他神经元的信号,也可以接收自己的反馈信号;
- 反馈网络在不同的时刻具有不同的状态,具有记忆功能;
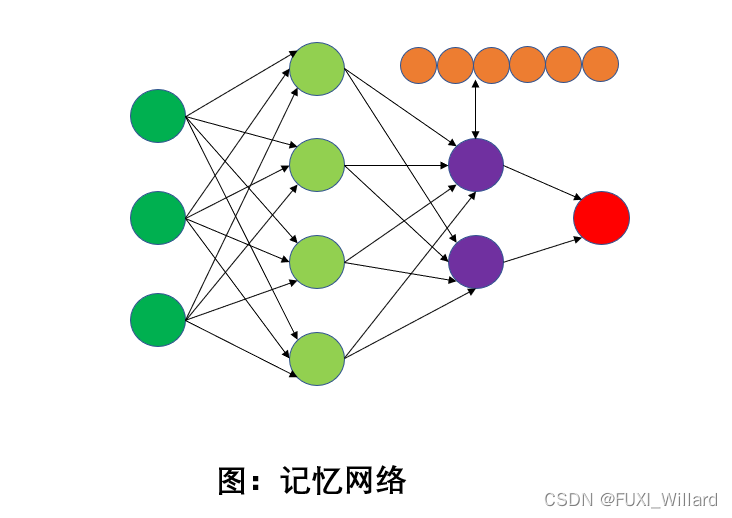
- 记忆网络;
- 记忆网络在前馈网络或反馈网络基础上,引入一组记忆单元,用保存中间状态;
- 记忆网络具有比反馈网络更强的记忆功能;
2.3 深度前馈网络
-
前馈神经网络中,各神经元分别属于不同层;
-
每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层;
-
第一层为输入层,最后一层为输出层,其他中间层为隐藏层;
-
整个网络无反馈,信号从输入层向输出层单向传播;
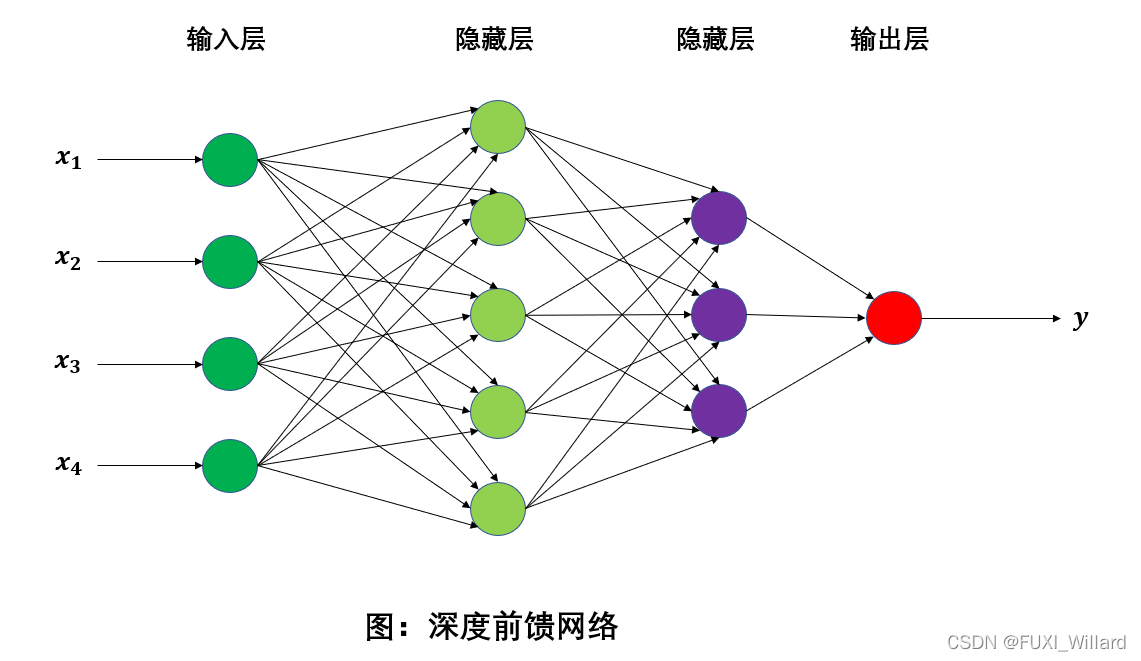
- L L L:表示神经网络的层数;
- n l n^l nl:表示第 l l l层神经元的个数;
- f l ( ? ) f_l(·) fl?(?):表示 l l l层神经元的激活函数;
- W ( l ) ∈ R n l × n l ? 1 W^{(l)}\in{R^{n^l\times{n^{l-1}}}} W(l)∈Rnl×nl?1:表示 l ? 1 l-1 l?1层到第 l l l层的权重矩阵;
- b ( l ) ∈ R n l b^{(l)}\in{R^{n^l}} b(l)∈Rnl:表示 l ? 1 l-1 l?1层到第 l l l层的偏置;
- z ( l ) ∈ R n l z^{(l)}\in{R^{n^l}} z(l)∈Rnl:表示 l l l层神经元的净输入;
- a ( l ) ∈ R n l a^{(l)}\in{R^{n^l}} a(l)∈Rnl:表示 l l l层神经元的输出;
前馈神经网络信息传播的公式:
z ( l ) = W ( l ) a ( l ? 1 ) + b ( l ) ; a ( l ) = f l ( z ( l ) ) z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)};a^{(l)}=f_l(z^{(l)}) z(l)=W(l)a(l?1)+b(l);a(l)=fl?(z(l))
2.4 参数学习
深度前馈神经网络中, ( W , b ) (W,b) (W,b)是模型参数,给定输入和输出数据对 ( x , y ) (x,y) (x,y),得到模型参数的过程称为训练或学习;
交叉熵损失函数实例:
- 函数表示
L ( y , y ^ ) = ? y T log ? y ^ , y ^ 为 对 应 的 o n e ? h o t 向 量 表 示 L(y,\hat{y})=-y^T\log{\hat{y}},\hat{y}为对应的one-hot向量表示 L(y,y^?)=?yTlogy^?,y^?为对应的one?hot向量表示 - 给定训练集:
D
=
{
(
x
(
i
)
,
y
(
i
)
)
}
,
1
≤
i
≤
N
D=\{{(x^{(i)},y^{(i)})}\},1≤i≤N
D={(x(i),y(i))},1≤i≤N,将每个样本
x
(
i
)
x^{(i)}
x(i)输入给前馈网络,得到网络输出
y
^
\hat{y}
y^?,其在数据集
D
D
D上的风险函数为:
R
(
W
,
b
)
=
1
N
∑
i
=
1
N
L
(
y
(
i
)
,
y
^
(
i
)
)
+
1
2
λ
∣
∣
W
∣
∣
F
2
R(W,b)=\frac{1}{N}\sum^{N}_{i=1}L(y^{(i)},\hat{y}^{(i)})+\frac{1}{2}\lambda||W||^2_F
R(W,b)=N1?i=1∑N?L(y(i),y^?(i))+21?λ∣∣W∣∣F2?
- W 和 b W和b W和b包含了每一层的权重矩阵和偏置向量;
- ∣ ∣ W ∣ ∣ F 2 ||W||^2_F ∣∣W∣∣F2?是正则化项,用来防止过拟合;
- λ \lambda λ是正数的超参数; λ \lambda λ越大, W W W越接近0;
- 网络参数通过梯度下降法进行学习;在梯度下降每次迭代中,第
l
l
l层的参数
W
(
l
)
W^{(l)}
W(l)和
b
(
l
)
b^{(l)}
b(l)更新方式:
W ( l ) ← W ( l ) ? α ? R ( W , b ) ? W ( l ) = W ( l ) ? α ( 1 N ∑ i = 1 N ? L ( y ( i ) , y ^ ( i ) ) ? W ( l ) + λ W ( l ) ) W^{(l)}\leftarrow{W^{(l)}}-\alpha\frac{\partial{R(W,b)}}{\partial{W^{(l)}}}=W^{(l)}-\alpha(\frac{1}{N}\sum^{N}_{i=1}\frac{\partial{L(y^{(i)},\hat{y}^{(i)}})}{\partial{W^{(l)}}}+\lambda{W^{(l)}}) W(l)←W(l)?α?W(l)?R(W,b)?=W(l)?α(N1?i=1∑N??W(l)?L(y(i),y^?(i))?+λW(l))
b ( l ) ← b ( l ) ? α ? R ( W , b ) ? b ( l ) = b ( l ) ? α ( 1 N ∑ i = 1 N ? L ( y ( i ) , y ^ ( i ) ) ? b ( l ) ) b^{(l)}\leftarrow{b^{(l)}}-\alpha\frac{\partial{R(W,b)}}{\partial{b^{(l)}}}=b^{(l)}-\alpha(\frac{1}{N}\sum^N_{i=1}\frac{\partial{L(y^{(i)},\hat{y}^{(i)})}}{\partial{b^{(l)}}}) b(l)←b(l)?α?b(l)?R(W,b)?=b(l)?α(N1?i=1∑N??b(l)?L(y(i),y^?(i))?)
α \alpha α为学习率;