问题 对于具有类别标签的数据,应当如何设计目标函数使得降维的过程中不损失类别信息?在这种目标下,应当如何进行求解?
LDA
首先是为了分类服务的,因此只要找到一个投影方向
ω
,使得投影后的样本尽可能按照原始类别分开。我们不妨从一个简单的二分类问题出发,有C
1
、C2两个类别的样本,两类的均值分别为


我们希望投影之后两类之间的距离尽可能大,距离表示为??
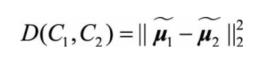
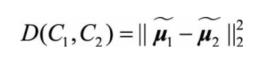

?
容易发现,当
ω
方向与(
μ
1
?
μ
2
)一致的时候,该距离达到最大值,例如对图4.5(
a
)的黄棕两种类别的样本点进行降维时,若按照最大化两类投影中心距离的准则,会将样本点投影到下方的黑线上。但是原本可以被线性划分的两类样本,经过投影后有了一定程度的重叠,这显然不能使我们满意。
我们希望得到的投影结果如图
4.5
(
b
)所示,虽然两类的中心在投影之后的距离有所减小,但确使投影之后样本的可区分性提高了。仔细观察两种投影方式的区别,可以发现,在图4.5
(
b
)中,投影后的样本点似乎在每一类中分布得更为集中了,用数学化的语言描述就是每类内部的方差比左图中更小。这就引出了LDA
的中心思想——
最大化类间距离和最小化类内距离。

Fisher LDA
相比
PCA
更善于对有类别信息的数据进行降维处理,但它对数据的分布做了一些很强的假设,例如,每个类数据都是高斯分布、各个类的协方差相等。尽管这些假设在实际中并不一定完全满足,但LDA
已被证明是非常有效的一种降维方法。主要是因为线性模型对于噪声的鲁棒性比较
好,但由于模型简单,表达能力有一定局限性,我们可以通过引入核函数扩展LDA方法以处理分布较为复杂的数据。
问题 LDA和PCA作为经典的降维算法,如何从应用的角度分析其原理的异同?从数学推导的角度,两种降维算法在目标函数上有何区别与联系?
同样作为线性降维方法,
PCA是无监督的降维算法,而LDA
是有监督的降维算法。虽然在原理或应用方面二者有一定的区别,但是从这两种方法的数学本质出发,我们不难发现二者有很多共通的特性。
从
PCA
和
LDA
两种降维方法的求解过程来看,它们确实有着很大的相似性,但对应的原理却有所区别。
首先从目标出发,
PCA
选择的是投影后数据方差最大的方向。由于它是无监督的,因此PCA
假设方差越大,信息量越多,用主成分来表示原始数据可以去除冗余的维度,达到降维。而LDA
选择的是投影后类内方差小、类间方差大的方向。其用到了类别标签信息,为了找到数据中具有判别性的维度,使得原始数据在这些方向上投影后,不同类别尽可能区分开。
举一个简单的例子,在语音识别中,我们想从一段音频中提取出人的语音信号,这时可以使用PCA
先进行降维,过滤掉一些固定频率(方差较小)的背景噪声。但如果我们的需求是从这段音频中区分出声音属于哪个人,那么我们应该使用LDA
对数据进行降维,使每个人的语音信号具有区分性。
另外,在人脸识别领域中,
PCA
和
LDA都会被频繁使用。