HMM
含义
HMM(Hidden Markov Model), 中文称作隐含马尔科夫模型, 因俄国数学家马尔可夫而得名. 它一般以文本序列数据为输入, 以该序列对应的隐含序列为输出.
- 什么是隐含序列
序列数据中每个单元包含的隐性信息, 这些隐性信息之间也存在一定关联
EG:
import jieba.posseg as psg
text = "他喜欢看动画片"
# 对文本进行分词处理
res = psg.lcut(text,True)
print(res)
#[pair('他', 'r'), pair('喜欢', 'v'), pair('看', 'v'), pair('动画片', 'n')]
# 每个词对应的隐含序列为
hidden_sequence = ["r","v","v","n"]
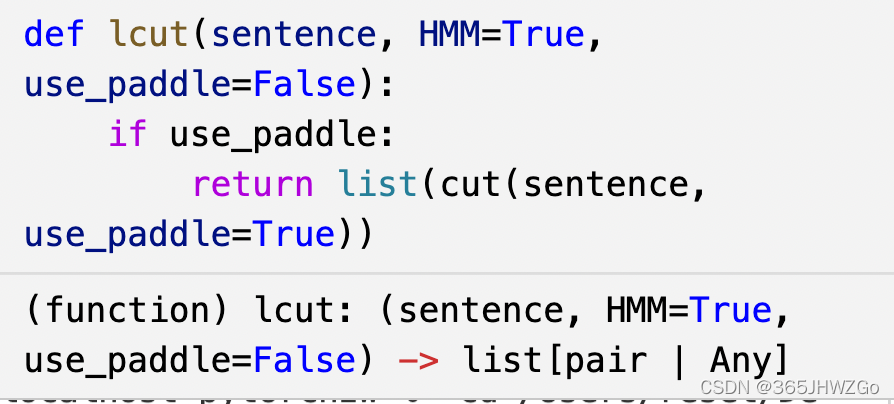
在posseg.lcut中可以看到隐马模型HMM,默认为True
作用
在NLP领域, HMM用来解决文本序列标注问题. 如分词, 词性标注, 命名实体识别都可以看作是序列标注问题.
隐含假设
隐含序列中每个单元的可能性只与上一个单元有关
使用过程
- 首先, HMM模型表示为: lambda = HMM(A, B, pi), 其中A, B, pi都是模型的参数, 分别称作: 转移概率矩阵, 发射概率矩阵和初始概率矩阵.
- 接着, 我们开始训练HMM模型, 语料就是事先准备好的一定数量的观测序列及其对应的隐含序列, 通过极大似然估计求得一组参数, 使由观测序列到对应隐含序列的概率最大.
状态序列隐藏的马尔可夫链随机生成的状态的序列
观测序列每个状态生成一个观测,而由此产生的观测的随机序列
- 在训练过程中, 为了简化计算, 马尔可夫提出一种假设: 隐含序列中每个单元的可能性只与上一个单元有关. 这个假设就是著名的隐含假设.
- 训练后, 我们就得到了具备预测能力的新模型: lambda = HMM(A, B, pi), 其中的模型参数已经改变.
- 之后给定输入序列(x1, x2, …, xn), 经过模型计算lambda(x1, x2, …, xn)得到对应隐含序列的条件概率分布.
- 最后, 使用维特比算法从隐含序列的条件概率分布中找出概率最大的一条序列路径就是我们需要的隐含序列: (y1, y2, …, yn).
维特比算法
本质:动态规划实现最短路径
维特比算法是
多步骤每步多选择模型的最优选择问题,其在每一步的所有选择都保存了前续所有步骤到当前步骤当前选择的最小总代价(或者最大价值)以及当前代价的情况下前继步骤的选择。依次计算完所有步骤后,通过回溯的方法找到最优选择路径。符合这个模型的都可以用viterbi算法解决,隐马模型的第三问题刚好符合这个模型,所以才采用了viterbi算法。
详情见知乎
通俗地讲解 viterbi 算法