[人工智能] 决策树从理论到实践

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 决策树从理论到实践 -> 正文阅读

[人工智能]决策树从理论到实践

决策树是一种基于分治的非线性分类算法。决策树的思想类似于二叉搜索树，即对决策树询问一些问题来对样本进行分类。
生成决策树在周志华老师的西瓜书中的伪代码参考如下。
在这里插入图片描述
这段代码不难，简单分析：

使用递归算法生成决策树。在样本数比较多的时候，程序效率可能不会很好，同时可能会爆栈。可以使用BFS或者DFS进行改写。

递归的返回终点严格来说分别有4种。
第1种，当前的分支结点，我们发现所有样本的类别都相同，那么很简单，不需要分类了，全部归为同一类。
第2种，分类属性为空，即第二个判断中的A= $\varnothing$ ，我们发现当前结点中没有属性可以进行划分了，那么我们当前结点应该归为哪一类呢？这里就取当前结点中类别样本多的那一类。
第3种，D中样本在A上的取值相同。这里不太好理解，我的理解是，D中的两个或多个样本，在A的属性集中的取值一样，但是最终的分类结果不一样，就是说出现相同的属性值，但是标签不一样，这个时候我们一样取类别样本值多的那一个。
第4种，在循环中返回。这里的意思是，遍历最佳属性的属性值为当前结点生成子节点，如果生成的子节点的样本集为空，那么就不往下划分了，直接把自己这一类标记为父节点的类型，返回，否则继续递归向下划分。
为什么循环中的这个返回不放到函数的最开始来判断呢？这和书中后面说的第2种分类情况和第4种分类情况不一样有关。因为放到外面进行返回，你只能标记为当前节点中样本数最多的类型，但是在后面的循环中进行返回，这个时候你是有父节点的样本的。而当前的节点样本数为空，那不就只能拿父节点的样本标签来标记嘛。
不过有一点没有想明白的是，最后一种递归返回情况的return语句，感觉改成continue会更好，如果遍历的属性值顺序不同，那得到的结果岂不是不同，直接return的话，该属性值上的其他情况都不会再考虑了。或者如果在前面加个sort，根据划分的数据集数量排下序，也是可以的。

决策树的关键在于上述代码的第8行，即我们如何选择一个最优的划分属性呢？根据不同的划分方法，产生了不同的决策树算法。
ID3算法使用信息增益Gain进行划分。C4.5算法使用Gain_ratio进行划分。CART决策树使用Gini指数进行划分。

用什么做为依据来选择一个最佳的属性进行划分呢？
一个好的划分使得决策树随着划分后面的节点尽可能地属于同一个类别，就是每个节点的纯度更高。纯度高，也就是包含的信息少，其实就是信息熵越小。所以简单的方法就是直接基于信息熵进行划分。
$Ent(D)=-\sum_{k=1}^{|y|}p_{k}log_2p_k$
信息熵越小，D的纯度越高。
基于信息熵，可以定义出信息增益 $G a i n (D, a)$
$Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{|D_{v}|}{|D|}Ent(D_{v})$
其中， $D_v$ 是样本集 $D$ 根据划分属性 $a$ 划分的 $V$ 个不同子集。
信息增益反映了划分后的信息熵变化情况。划分之后每个节点越纯，那么信息熵就越小，根据上面的公式，信息增益就越大。即我们可以遍历每一个属性值a，分别求出每一个属性的信息增益，取最大的作为当前的划分属性。
显然，信息增益对划分集合个数多的节点有所偏好，极端情况就是，每个区间只有一个样本，熵为0，但这样的决策树泛化能力不好。所以引入 $I V (a)$ 定义增益率 $Gain\_ratio(D,a)$ ,
$IV(a)=-\sum_{v=1}^V\frac{|D_v|}{|D|}log_2\frac{|D_v|}{|D|}$
IV(a)对划分集合数少的属性有所偏好，通常情况下， $V$ 越大， $I V (a)$ 就越大。
C4.5算法中使用的增益率 $Gain\_ratio(D,a)$ 进行划分，
$Gain\_ration(D,a)=\frac{Gain(D,a)}{IV(a)}$
而在CART决策树中，采用了基尼指数 $Gini\_index$ 进行划分属性的选择。
$Gini(D)=\sum_{k=1}^{|y|}\sum_{k'\neq k}p_kp_{k'}$
$G i n i (D)$ 反映了从数据集中随机抽取两个样本，其标记类别不一致的概率，所以 $G i n i (D)$ 越小，则数据集D的纯度就越高，这和信息熵是一致的。
基尼指数定义为：
$Gini\_index(D,a)=\sum_{v=1}^V\frac{|D_v|}{|D|}Gini(D_v)$

基于以上算法，我们就可以根据数据集构造一棵决策树了。但是为了防止决策树出现过拟合的情况，我们需要对决策树进行剪枝处理，周志华老师书上提到的剪枝方法有两种，分别是预剪枝和后剪枝。预剪枝是在生成决策树的过程中进行剪枝，后剪枝是在生成完整个决策树后，再进行剪枝。预剪枝在生成决策树过程中，尝试不对节点进行划分，即剪枝，然后使用验证集进行验证，计算是否剪枝带来了正确率的提高。后剪枝有REP，PEP，CCP等多种方法，这里就不详细说明了，具体可以参考这篇博客。决策树的剪枝算法

决策树的一些问题

多变量决策树

决策树实践

以上就是决策树的理论部分，下面将以两个个具体的实践例子，动手实现决策树来理解决策树。
第一个例子是直接使用sklearn中的现成函数直接生成。可以参考这篇博客，决策树的应用
直接调个函数就完成了，这显然不是我们想要的效果，但是还是可以跟着代码实现一下，感受一下，也是非常有帮助的。

第二个例子就是西瓜书的课后习题，4.3. 参考了这篇文章西瓜书课后习题
1. 导包与预处理数据
所使用的python版本为python3.8

import numpy as np
import pandas as pd
import math
import copy
import matplotlib.pyplot as plt
import matplotlib as mpl
import copy

所使用的数据直接贴出

编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

接着就是读入csv数据，并转换为矩阵matrix

dataset = pd.read_csv('./watermelon_3.csv',delimiter=",")
Attributes = dataset.columns
m,n=np.shape(dataset)
dataset=np.matrix(dataset)

接着提取属性结合，其中Attributes为所有的属性名字，而attributeset表示所有的属性可能取值集合。
D为数据的序号列表，A的维度为n，值为1或-1，来表示当前这个属性是否可用。

attributeset=[]
for i in range(n):
    curset=set()
    for j in range(m):
        curset.add(dataset[j,i])
    attributeset.append(curset)
EPS=0.000001
D=np.arange(0,m,1)
A=np.ones(n)
A=list(A)
A[0]=A[n-1]=-1
A,D

2.定义决策树节点

class Node(object):
    def __init__(self,title):
        self.title=title
        self.v="是"
        self.children=[]
        self.deep=0
        self.ID=-1

其中，title表示当前结点的名字，v表示当前的结点的属性，children是结点的孩子结点列表，deep表示当前结点的深度，ID是结点的序号
3.生成决策树

def TreeGenerate(D,A,title):
    node = Node(title)
    if isSameY(D):
        node.v = dataset[D[0],n-1]
        return node
    if isblank(A) or issameAinD(D,A):
        node.v = mostCommonY(D)
        return node
    ent=0  #最大熵
    floatv=0  #划分值
    p=0    #存储属性下标
    for i in range(len(A)):
        if A[i]>0:
            cur,div=gain(D,i)
            if cur > ent:
                p=i
                ent = cur
                floatv=div
    if isSameValue(-1000,floatv,EPS): #离散属性
        node.v=Attributes[p]+"=?"
        curset=attributeset[p]
        for i in curset:
            Dv=[]
            for j in range(len(D)):
                if dataset[D[j],p]==i:
                    Dv.append(D[j])
            if Dv==[]:
                nextNode=Node(i)
                nextNode.v=mostCommonY(D)
                node.children.append(nextNode)
            else:
                newA=copy.deepcopy(A)
                newA[p]=-1
                node.children.append(TreeGenerate(Dv,newA,i))
    else:
        Dleft=[]
        Dright=[]
        node.v=Attributes[p]+"<="+str(floatv)+"?"
        for i in range(len(D)):
            if dataset[D[i],p]<=floatv:
                Dleft.append(D[i])
            else:Dright.append(D[i])
        node.children.append(TreeGenerate(Dleft,A[:],1))
        node.children.append(TreeGenerate(Dright,A[:],0))
    return node

其过程和开头的伪代码是一样的，只不过是用python实现了。需要注意的是，生成的过程中，离散属性和连续属性要分开处理，并且在处理连续属性的时候，不需要对A列表进行处理，这是因为连续属性是可以在子树中继续使用。
上面的代码中，需要还需要完善isSameY(判断D中所有样本是否属于同一类)、isblank(属性A中可用的元素是否为空)等各种函数，这里就不详细说明了，其原理其实很好理解。
4.完善函数

def isSameY(D):
    curY=dataset[D[0],n-1]
    for i in range(1,len(D)):
        if dataset[D[i],n-1]!=curY:
            return False
    return True
    
def isblank(A):
    for i in range(n):
        if A[i]>0:return False
    return True
    
def isSameValue(a,b,eps):
    if(type(a)==type(dataset[0,8]) or type(a)==type(dataset[0,7])):
        return abs(a-b)<eps
    else : return a==b
    
def issameAinD(D,A):
    for i in range(n):
        if A[i]>0:
            for j in range(1,len(D)):
                if not isSameValue(dataset[D[0],i],dataset[D[j],i],EPS):
                    return False
    return True
    
def mostCommonY(D):
    res = dataset[D[0],n-1]
    mx=1
    count={}
    count[res]=1
    for i in range(1,len(D)):
        cur = dataset[D[i],n-1]
        if cur not in count:
            count[cur]=1
        else:count[cur]+=1
        if count[cur]>mx:
            mx=count[cur]
            res=cur
    return res   #最多的类别是Yes or No
    
def Ent(D):
    
    types=[]
    count={}
    
    for i in range(len(D)):
        curY = dataset[D[i],n-1]
        if curY not in count:
            count[curY]=1
            types.append(curY)
        else:
            count[curY]+=1
    ans=0
    print(types)
    total = len(D)
    for i in range(len(types)):
        ans-=count[types[i]]/total*math.log2(count[types[i]]/total)
    return ans
    
def gain(D,a):
    if type(dataset[0,a])==type(dataset[0,8]) or type(dataset[0,a])==type(dataset[0,7]):
        res,div=gainfloat(D,a)  #div为划分点
    else:
        types = []
        count = {}
        for i in range(len(D)): #为了得到每一个属性取值的样本编号
            p = dataset[D[i],a]
            if p not in count:
                count[p]=[D[i]]
                types.append(p)
            else:
                count[p].append(D[i])
        res=Ent(D)
        total=len(D)
        for i in range(len(types)):
            res-=len(count[types[i]])/total*Ent(count[types[i]])
        div=-1000    #划分点任取，离散和连续不同
    return res,div  
    
def gainfloat(D,a): #连续属性的Gain(D,a)
    p=[]
    for i in range(len(D)):
        p.append(dataset[D[i],a])
    p.sort()
    T=[]
    for i in range(len(p)-1):
        T.append((p[i]+p[i+1])/2)
    res=Ent(D)
    ans = 0
    div=T[0]
    for i in range(len(T)): #以T[i]作为划分点，分为大于和小于两类
        left=[]
        right=[]
        for j in range(len(D)):
            if(dataset[D[j],a]<=T[i]):
                left.append(D[j])
            else:right.append(D[j])
        tmp = res-Ent(left)*len(left)/len(D)-Ent(right)*len(right)/len(D)
        if tmp > ans:
            div = T[i]
            ans=tmp
    return ans,div

5.可视化决策树
首先生成一棵决策树

myDecisionTreeRoot = TreeGenerate(D,A,"root")

计算决策树的深度和叶子结点数量

def countleaf(root,deep):
    root.deep=deep
    res=0
    #print(1)
    if root.v==1 or root.v == 0 :
        res+=1
        return res,deep
    curdeep=deep
    for i in root.children:
        a,b=countleaf(i,deep+1)
        res+=a
        if b>curdeep:
            curdeep = b
    return res,curdeep
    
cnt,deep = countleaf(myDecisionTreeRoot,0)

为每个结点标上ID

def giveleafid(root,id):
    
    if root.v=="是" or root.v=="否":
        root.ID=id
        id+=1
        return id
    for i in root.children:
        id =giveleafid(i,id)
    return id
    
giveleafid(myDecisionTreeRoot,0)

遍历决策树进行画图，后面是一些对画图的参数调整。

def dfsPlot(root):
    #print(cnt)
    if root.ID==-1:          # 说明根节点不是叶子节点
        childrenPx = []
        meanPx = 0
        for i in root.children:
            cur = dfsPlot(i)
            meanPx += cur
            childrenPx.append(cur)
        meanPx = meanPx/len(root.children)
        c = 0
        for i in root.children:
            nodetype = leafNode
            if i.ID<0: nodetype=decisionNode
            plotNode(i.v,(childrenPx[c],0.9-i.deep*0.8/deep),(meanPx,0.9-root.deep*0.8/deep),nodetype)
            plt.text((1.5*childrenPx[c]+0.5*meanPx)/2,(0.9-i.deep*0.8/deep+0.9-root.deep*0.8/deep)/2,i.title)
            c += 1
        return meanPx
    else:
        return 0.1+root.ID*0.8/(cnt-1)
        
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
    plt.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext=centerPt,
            textcoords='axes fraction',va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)

decisionNode = dict(boxstyle = "sawtooth",fc = "0.9",color='blue')
leafNode = dict(boxstyle = "round4",fc="0.9",color='red')
arrow_args = dict(arrowstyle = "<-",color='green')
fig = plt.figure(1,facecolor='white')
rootX = dfsPlot(myDecisionTreeRoot)
plotNode(myDecisionTreeRoot.v,(rootX,0.9),(rootX,0.9),decisionNode)
plt.show()

最后要注意的是，决策树中的中文可能会乱码，需要再加上两行代码。

mpl.rcParams[u'font.sans-serif'] = ['simhei']
mpl.rcParams['axes.unicode_minus'] = False

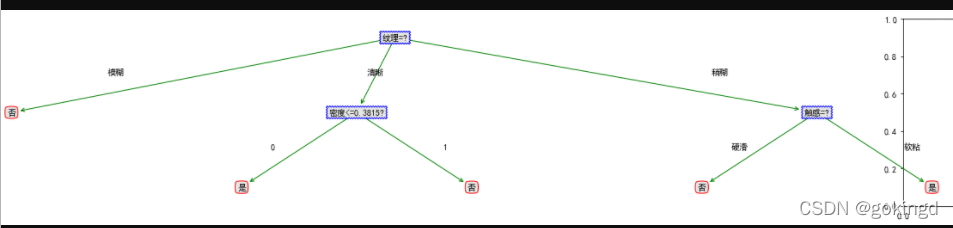
最后的效果图：
请添加图片描述

References：

周志华著. 机器学习, 北京: 清华大学出版社, 2016年1月.
https://blog.csdn.net/qq_37691909/article/details/85235472

人工智能最新文章

2022吴恩达机器学习课程——第二课（神经网

第十五章规则学习

FixMatch: Simplifying Semi-Supervised Le

数据挖掘Java——Kmeans算法的实现

大脑皮层的分割方法

【翻译】GPT-3是如何工作的

论文笔记:TEACHTEXT: CrossModal Generaliz

python从零学（六）

详解Python 3.x 导入(import)

【答读者问27】backtrader不支持最新版本的

加:2021-12-09 11:39:17 更:2021-12-09 11:39:20

360图书馆购物三丰科技阅读网日历万年历 2024年11日历

-2024/11/27 1:26:20-

图片自动播放器
↓图片自动播放器↓

TxT小说阅读器
↓语音阅读,小说下载,古典文学↓

一键清除垃圾
↓轻轻一点,清除系统垃圾↓

图片批量下载器
↓批量下载图片,美女图库↓

网站联系: qq:121756557 email:121756557@qq.com IT数码