[人工智能]深度学习的实用层面＜吴恩达深度学习_第2课_week1＞

1. 数据分类

数据一般分为<训练集(train)、验证机(dev)、测试集(test)>
其中，验证集的作用是选择最好的模型，测试集用来评估。

（1）当数据量较小时（100、1000、1000）

数据一般按照以下比例

(2) 当数据量较大时（几十万，百万级）

数据一般按照以下比例

或者：

2. 方差（variance）和偏差(bias)

（1）区别

方差是预测值自身的一个指标，而偏差是预测值和真实值的一个指标。

（2） 示例

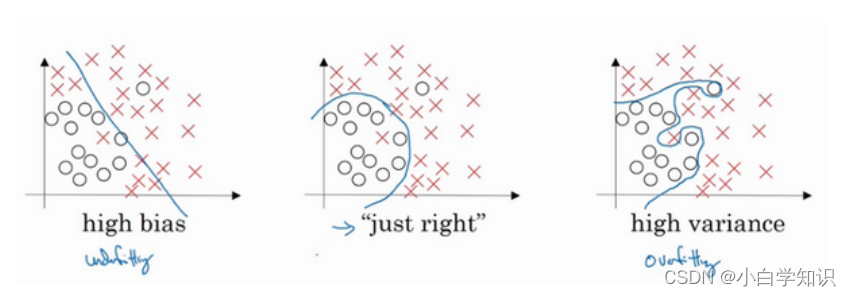
3. 各种情形的处理方式

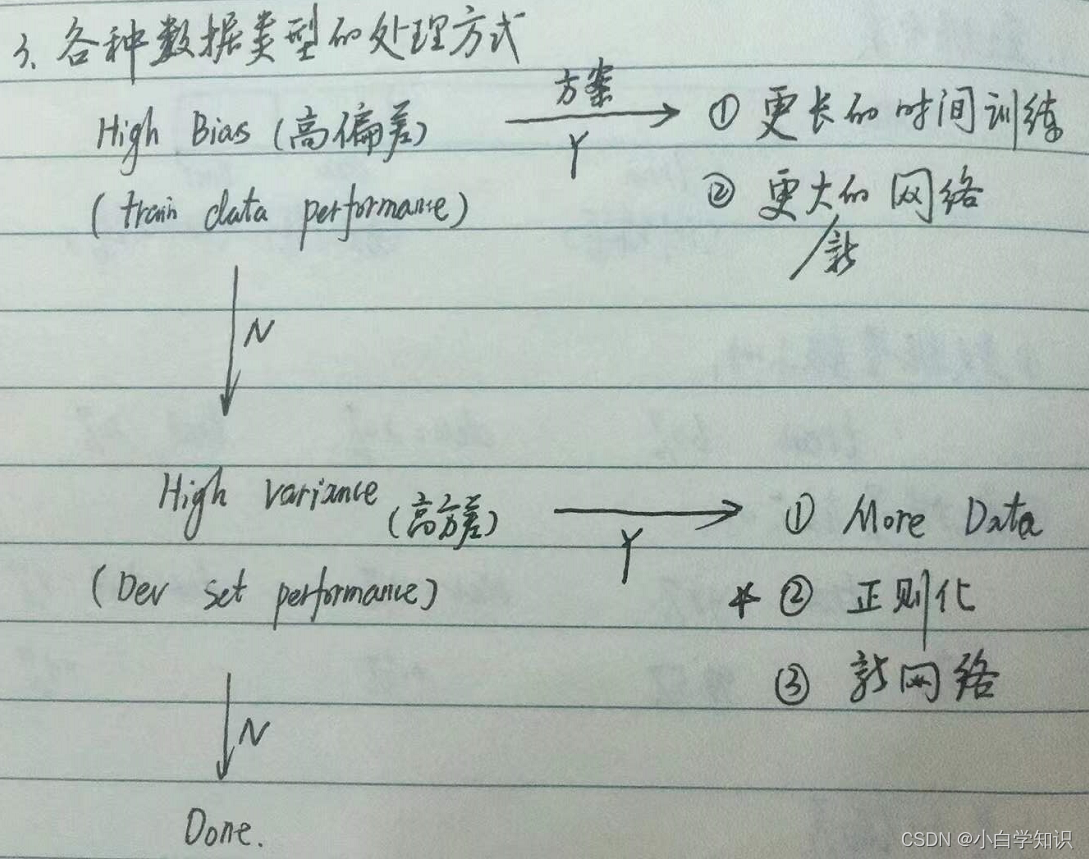
4. 正则化

（1）正则化作用

深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。

（2）$L2$ 正则化

$$J(w,b)=\frac{1}{2}\sum _{i=1}^{m}L({\hat{y}}^i,y^i)+\frac{\lambda }{2m}||w|{|}_2^2$$
其中：
$\lambda$ ：正则化参数，通常使用验证机来配置这个参数
$||w|{|}_2^2$ ：欧几里得范数（2范数）的平方，其中：
$$||w|{|}_2^2=\underset{j=1}{\sum ^n}{w}_j^2=w^{T}w$$

5. 神经网络中实现$\lambda 2$正则化

??神经网络中包含一个成本函数，该函数包含$w^{[1]},b^{[1]},...,w^{l1]},b^{[l]}$所有参数，字母$l$是神经网络的层数，因此成本函数等于$m$个训练样本损失函数的总和乘以$\frac{1}{m}$， 正则项为 $\frac{\lambda }{2m}\underset{1}{\sum ^L}|w^{[l]}{|}^2$，我们称之为$||w^{[l]}|{|}^2$平方范数，这个矩阵范数被定义为矩阵中所有元素的平方求和
$$J(w^{[1]},b^{[1]},...,w^{[L]},b^{[L]})=\frac{1}{m}\underset{i=1}{\sum ^m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}\underset{l=1}{\sum ^L}||w^{[l]}|{|}_F^2$$
??其中，F: 表示“弗罗贝尼乌斯范数”，用下标 F 标注”，无计算意义；
$$||w^{[l]}|{|}_F^2=\underset{i=1}{\sum ^{n^{[l?1]}}}\underset{j=1}{\sum ^{n^{[l]}}}(w_{ij}^{[l]}{)}^2$$