分类技术——二分网络上的链路预测
实验内容
采用二分网络模型,对ml-1m文件夹中的“用户—电影”打分数据进行建模,考虑将用户信息、电影详细信息、以及打分分值作为该网络上的边、点的权重;
根据网络结构特征给出节点相似性度量指标;
基于相似性在二分网络上进行链路预测;
画出ROC曲线来度量预测方法的准确性 ;
详细实现
-
导入数据包.py
import pandas as pd ''' 该文件是将数据包中的ratings.dat导入到python中; 导入后在python中的保存形式:<class 'pandas.core.frame.DataFrame'>; 该文件仅对ratings.dat文件做了数据导入处理,因为后面仅用了这一个文件的信息(电影打分相似度)来推荐电影; 如果想要得到更精确的结果,可以导入其他两个文件,计算出不同的相似度矩阵(例如:性别相似度,电影类别相似度等); ''' # 用字符串保存文件路径 ratings_path = './数据包/ratings.dat' # pandas中的read_table函数可以读取.dat文件;(read_csv函数貌似也可以,结果似乎没什么不同) # 设置列名:"UserID(用户ID)", "MovieID(电影ID)", "Rating(评分)", "Timestamp(时间戳)" ratings_names = ["UserID", "MovieID", "Rating", "Timestamp"] all_ratings = pd.read_table(ratings_path, sep='::', engine='python', names=ratings_names) # 时间戳可以用pd中的to_datetime处理,虽然本实验没有用到; # all_ratings['Datetime'] = pd.to_datetime(all_ratings['Timestamp']) # 测试输出,输出读取数据的前五个; # print(all_ratings[:5]) # 另一种输出方式:打印前n条数据, 缺省默认是5; # print(all_ratings.head(6)) -
数据处理.py
import numpy as np from 实验一电影推荐 import 导入数据包 as sj ''' 该文件实现功能; 对导入的数据进行处理,最终生成权重矩阵W; 矩阵W:行代表用户i,列代表电影j,值代表用户i给电影j的打分分值转换的权重; ''' # rand()返回一组均匀分布(服从[0,1)分布)的随机数; random()返回一个随机生成的实数,范围在[0,1); # mask是一个只包含True和False的矩阵,这个数组是让你指定需要掩盖的值的,标记为True的数据会被掩盖掉。 mask = np.random.rand(len(sj.all_ratings)) < .9 # print(mask) # 90%数据用于训练,10%数据用于测试,用mask掩盖矩阵进行划分; train_ratings = sj.all_ratings[mask] test_ratings = sj.all_ratings[~mask] ''' 一共有多少部电影和多少个用户; all_ratings中存有有效的(评过分的)UserID和MovieID 但是all_ratings中包含是重复的ID,若使用需要先用unique()去重后再len(); ''' r_users = sj.all_ratings["UserID"].unique() r_movies = sj.all_ratings.MovieID.unique() users_size = len(r_users) movies_size = len(r_movies) ''' 对用户ID和电影建立索引; 原因:原始数据中用户和电影并不是按顺序存储的(甚至ID都不是按顺序存在的,可能某一处99之后就是101); k代表索引,uid、mid代表ID,enumerate是建立索引的函数,{}里的写法类似与三元表达式; ''' uid2idx = {uid: k for k, uid in enumerate(r_users)} mid2idx = {mid: k for k, mid in enumerate(r_movies)} ''' 用户对电影的评分(score)范围为[1,5],没看过的电影可以认为评分为0,可以将评分转化为权重w; 一种权重转换方法: w = score / 5;w 范围为[0,1];(AUC = 0.85左右,效果不太理想) (可能是因为太过于均分权重,五个评分1星的电影相当于一个评分五星的电影,这显然是不合理的) 另一种转换方法: 将w设计为一个score的函数(下凸的)或者用一个列表来存储score和w的转化; 建立W矩阵,行为用户i,列为电影j,值为权重w; ''' # 用一个列表存score和w的对应关系(可以修改列表的值来追求更高的AUC) movies_w = [0, 0.000001, 0.0001, 0.01, 0.1, 1] # AUC = 0.911 # movies_w = [0, 0, 0, 0, 0, 1] # AUC = 0.9088 # 初始化一个我们需要的shape的,值全为0的矩阵W W = np.zeros((users_size, movies_size)) for _, rating in train_ratings.iterrows(): W[uid2idx[rating.UserID], mid2idx[rating.MovieID]] = movies_w[rating.Rating] # W[uid2idx[rating.UserID], mid2idx[rating.MovieID]] = 15 ** (rating.Rating - 5.0) ''' 改变score对应的w值,发现评分为4星的权重越低,AUC反而越好(AUC最大和最小差距在0.05左右); 从结果来看,似乎代表:一个电影被评4星,代表用户就喜欢类似的电影程度不高;一个电影被评5星,才能较大程度说明用户的喜好。 但是按照常理来说,4星的评分已经相对较高了,应该可以很大程度代表用户的喜好了。 这里面的原因不太了解。 ''' -
相似度设定.py
import numpy as np from 实验一电影推荐 import 数据处理 as sjcl ''' 相似度矩阵是预测的关键,可以从多个维度建立相似度矩阵; Sim_1是从评分的角度建立的相似度关系,也就是电影的评分相似度; 用矩阵乘法根据推导出的Sim_1的公式进行计算; 我们还可以尝试在性别、电影类别等角度建立相似度矩阵(多个二部图),最后将所有的相似度矩阵分别乘以系数相加,得到总体的预测率更高的相似度矩阵; ''' # 计算第一个相似度 sim_1 W = sjcl.W # 关于sum函数:axis=0为列相加,axis=1为行相加; # movieJ_w 代表电影j被用户评价的全部权重w的和,userI_w 代表用户i评价的全部电影的权重w的和; movieJ_w = W.sum(axis=0) userI_w = W.sum(axis=1) # 相似度矩阵Sim应该是电影i和电影j的相似度的矩阵,所以初始化时行和列都是movies_size; Sim_1 = np.zeros((sjcl.movies_size, sjcl.movies_size)) # reshape()用于转化数组为列向量; W1 = W / userI_w.reshape((-1, 1)) # 会出现0/0的情况,所以用isnan转化Nan为0 W1[np.isnan(W1)] = 0 # dot():矩阵乘法,该处代表:矩阵W1的转置乘以矩阵W Sim_1 = np.dot(W1.T, W) Sim_1 = Sim_1 / movieJ_w Sim_1[np.isnan(Sim_1)] = 0 # print("Sim_1= ", Sim_1)

-
训练和测试.py
import numpy as np from 实验一电影推荐 import 数据处理 as sjcl, 相似度设定 as xsd ''' 该文件功能: 通过训练集生成"电影排序矩阵"; 生成测试集; 电影排序矩阵:行代表用户i,列代表电影j,值代表在用户i眼里电影j在所有电影里的排名; ''' u_size = sjcl.users_size m_size = sjcl.movies_size Sim = xsd.Sim_1 W = xsd.W # 建立推荐矩阵F和排序后的推荐矩阵F_sort ''' argsort()例子: F = [[0.1, 1, 1], [1, 0.2, 1]] F_sort_index = [[0 1 2], [1 0 2]] F_sort = [[3. 2. 1.], [2. 3. 1.]] ''' F = np.dot(Sim, W.T).T F_sort_index = np.argsort(F, axis=1) F_sort = np.zeros((u_size, m_size)) for i in range(u_size): for j in range(m_size): F_sort[i, F_sort_index[i][j]] = m_size - j # 初始化测试集(与初始化训练集类似); ''' 测试集中的评分我们转换为一个权重数组movies_w,数组里的值代表我们有多大程度希望推荐该星级的电影; 例如:movies_w[1],movies_w[2],movies_w[3]都设置为0,代表我们不希望推荐和1到3星的类似的电影; movies_w[4]=0.2,movie_w[5]=1,代表我们很希望推荐5星的电影; 同时对推荐4星电影的期望程度只有5星的五分之一; 如果可推荐的电影足够多的话,给用户推荐类似于5星显然更优; ''' movies_w = [0, 0, 0, 0, 0, 1] Test = np.zeros((u_size, m_size)) for _, rating in sjcl.test_ratings.iterrows(): # Test[sjcl.uid2idx[rating.UserID], sjcl.mid2idx[rating.MovieID]] = sjcl.movies_w[rating.Rating] Test[sjcl.uid2idx[rating.UserID], sjcl.mid2idx[rating.MovieID]] = movies_w[rating.Rating] # 指数函数的底:AUC值 —— 7:0.897288 8:0.8986 10:0.90186 15:0.9041 20.0.9057 # Test[sjcl.uid2idx[rating.UserID], sjcl.mid2idx[rating.MovieID]] = 15 ** (rating.Rating - 5.0) # print(Test) -
效果验证.py
from 实验一电影推荐 import 训练和测试 as tfianl import numpy as np import matplotlib.pyplot as plt ''' 输出ROC曲线; 输出AUC值; ''' Test = tfianl.Test F = tfianl.F_sort m_size = tfianl.m_size # TPR代表正例中被预测为正例的 # FPR代表负例中被预测为正例的 TPR, FPR = [], [] # 正样本,测试集的全部值相加,即全部打过分的电影的分数和; T_all = np.sum(Test) # 负样本,测试集中没被打过分的电影的数量,在负样本中,没被打过分的电影权值为1; F_all = np.sum(Test == False) for threshold in np.arange(0, 1, 0.005): F_out = F < (m_size * threshold) # 0,1矩阵,用于判断是排名靠前的还是靠后的,靠前为1,靠后为0,排名在threshold*movie_size之前的为靠前 # 由于threshold在改变,故分界线也在移动,一开始0多,后来1多; # F_out = F_out.astype(int) # 如果一个电影被评价了,且排名靠前(预测正确),则取(电影评价权值*1)相加;(正例中被预测为正例的) TP = np.sum(Test * F_out) # 如果一个电影没有被评价,且排名靠前(预测错误),则取(负样本权值1*1)=1相加;(负例中被预测为正例的) FP = np.sum((1 - Test) * F_out) TPR.append(TP / T_all) FPR.append(FP / F_all) # 画图(横坐标为FPR,纵坐标为TPR) plt.plot(FPR, TPR) plt.xlim(0, 1) plt.ylim(0, 1) plt.xlabel("FPR") plt.ylabel("TPR") plt.show() # ROC曲线的积分 # AUC值越接近1,预测效果越好; AUC = np.sum([0.005 * tpr for tpr in TPR]) print(AUC)
实验结果
(数据量为100万条左右的情况下,大概跑一次代码十分钟左右)
-
AUC输出值:
- 红色部分只是一个警告,因为在数组运算时出现了0/0=NaN的情况,可以忽略;

- 红色部分只是一个警告,因为在数组运算时出现了0/0=NaN的情况,可以忽略;
-
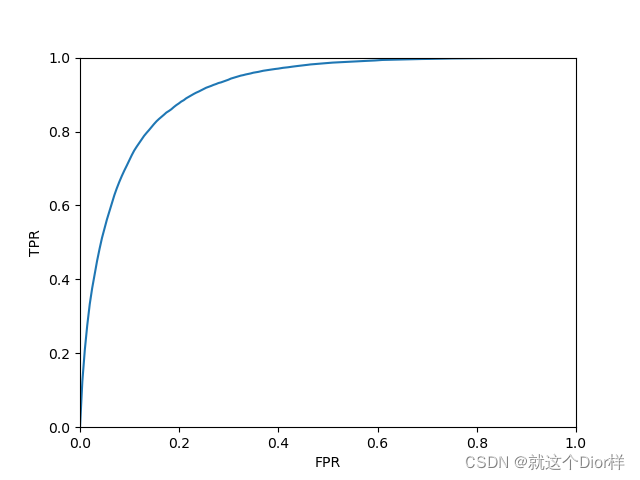
ROC曲线: