文章目录
摘要
文章提出了一个新的参数变换——投影变换和相似变换结合。给定两张输入图片的投影变换,基于投影变换分析,该方法计算重叠区域的投影变换和非重叠区域都是平滑的,并且结果的扭曲会从投影到相似逐渐改变。这种变换加强了投影和相似变换。,当图片作为相似变换时的透视效果被保护时,投影变换有很好的拼接准确度。也可以和更先进的基于局部扭曲的配准方法APAP结合达到更高的准确度。在这种方法下,拼接图的视野会扩大,投影损失更少。(形状拉伸,大小更大)
1.介绍
图像拼接是一个把几张图片结合成一张视野范围更广泛大图的过程。为了鲁棒性更强,图像拼接问题被很好地解决通过全局参数扭曲,使图片拼接更准。全局扭曲的广泛选择包括相似性,仿射和投影变换。尽管它们的鲁棒性很强,但是全局扭曲对于所有类型的场景和运动并不是足够灵活。例如,投影扭曲只在平面场景或无视差相机运动情况下才能配准。
为了解决全局扭曲模型不充足问题和改善匹配的准确度,最近有几种局部扭曲模型被提出,例如SVA、APAP。为了更好的准确度,而不是依赖单一全局扭曲,这些方法在重叠区域采用多局部参数扭曲来解决拼接不准的问题。对于非重叠区域,投影(仿射)正则化平滑地推算图像重叠以外的变换,类似于一个整体的全局变换。例如,APAP使用移动DLT局部投影变换平滑地在非重叠区域推算局部投影变换。因此,扭曲的结果是全局投影,允许局部脱离模型的不足。然而,虽然APAP类似于一个全局投影变换,它也有于投影变换相同的问题,就是形状/区域损失——拼接图的一部分拉伸严重,图片大小扩大的不统一。
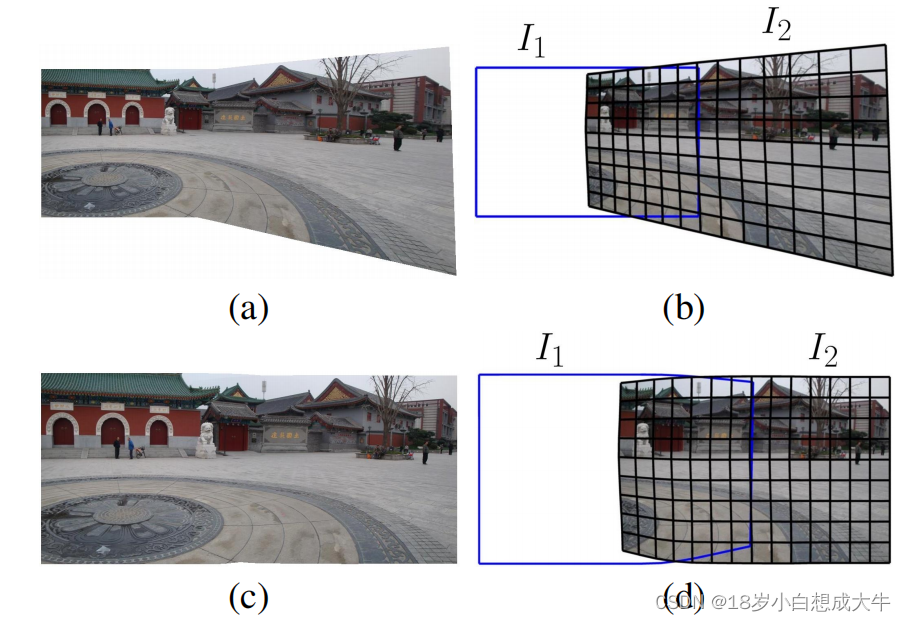
考虑到图1中传统的2视图问题,
I
1
I_1
I1?和
I
2
I_2
I2?是被拼接的两幅图,
I
1
I_1
I1?是基准图。图1(a)展示了APAP的结果。APAP局部调整不同的变换,因此在两幅图的重叠区域更准。图(b)展示了重叠区域变换被推算到非重叠区域并且结果扭曲近似于全局投影变换。当再有第三幅图和
I
2
I_2
I2?拼接在一起时,损失会进一步扩大。另一个值得关注的问题是,论文[7]中指出的,对
I
2
I_2
I2?应用投影扭曲能有效地改变它对
I
1
I_1
I1?的透视效果。因此,
I
2
I_2
I2?可以扭曲完作为
I
1
I_1
I1?的扩展。拼接图展示了更广的
I
1
I_1
I1?的透视视野而且是个单一透视。柱面和球面扭曲通过提供多透视视野解决了视野狭窄的问题。不幸的是,这些扭曲通过会弯曲直线而且只对在相同相机中心拍摄的图片有效。
尽管有广泛视野的单一透视图像不可避免严重的形状/大小损失,解决它必须土工多透视拼接图。初步的想法就是在重叠区域投影扭曲,在非重叠区域用相似扭曲保护每个视野的透视。我们选择投影扭曲因为它是最灵活的全局扭曲。另一方面,我们选择相似变换因为它只由平移、统一缩放和旋转
构成,而且无形状损失和不统一的大小。从另一种视角来看,相似变换可以看作镜头移动,改变焦距,平面内旋转的整合,保证了视野方法不变,从而保护了透视。另外,为了构建光滑扭曲,透视变换和相似变换之间需要光滑过渡。
本文提出一种新颖参数扭曲变换——保形半投影扭曲变换,投影变换和相似变换结合。这种结合同时考虑了配准的灵活和透视的保护。根据图1中的 I 1 I_1 I1?和 I 2 I_2 I2?,首先评估它们之间的全局投影变换。然后,通过新的投影变换方案来决定相似变换。直观地,我们的扭曲在重合区域执行了投影扭曲配准,相似变换保护了图像的非重叠区域。这种策略也用于平滑过渡透视和相似扭曲。我们也提出了策略整合了APAP。局部方法用APAP方法,生成多透视视图用该提出的方法。正如图1(c)(d)所示,使用结合的方式建立了多角度视图,配准很好。没有严重的大小改变,形状扭曲,直线弯曲。
2.相关工作
略。
3. 算法
( x , y ) (x,y) (x,y)映射到 ( x ′ , y ′ ) (x',y') (x′,y′),投影变换 H ^ \hat H H^,用直线把空间分成 R H R_H RH?和 R L R_L RL?,属于 R H R_H RH?的点 ( x , y ) (x,y) (x,y),有 w ( x , y ) = H ^ ( x , y ) ) w(x,y) = \hat H(x,y)) w(x,y)=H^(x,y))。另一半 R L R_L RL?,扭曲函数连续推算 H ^ \hat H H^直到变成相似变换 S S S。因为投影变换在一半空间,而保护形变在另一半空间,所以叫保形半投影扭曲变换。
3.1投影变换分析
扭曲变换的建立来自于给定的投影变换
H
^
\hat H
H^的分析。投影变换(单应变换)
H
^
:
(
x
,
y
)
→
(
x
′
,
y
′
)
\hat H:(x,y) \rightarrow(x',y')
H^:(x,y)→(x′,y′)定义为同一个坐标系下的线性变换:
[
x
′
y
′
1
]
~
[
h
1
^
h
2
^
h
3
^
h
4
^
h
5
^
h
6
^
h
7
^
h
8
^
1
]
[
x
y
1
]
(1)
\left[ \begin{matrix} x' \\ y' \\ 1 \end{matrix} \right] \sim \left[ \begin{matrix} \hat{h_1} & \hat{h_2} & \hat{h_3}\\ \hat{h_4} & \hat{h_5} & \hat{h_6} \\ \hat{h_7} & \hat{h_8} & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] \tag1
???x′y′1????~???h1?^?h4?^?h7?^??h2?^?h5?^?h8?^??h3?^?h6?^?1???????xy1????(1)
其中,
~
\sim
~表示在一个缩放范围内相等,它有8个参数。
(
x
,
y
)
(x,y)
(x,y)到
(
x
′
,
y
′
)
(x',y')
(x′,y′)映射可以重写为:
x
′
=
h
1
^
x
+
h
2
^
y
+
h
3
^
h
7
^
x
+
h
8
^
y
+
1
,
y
′
=
h
4
^
x
+
h
5
^
y
+
h
6
^
h
7
^
x
+
h
8
^
y
+
1
.
(2)
x' = \frac{\hat{h_1}x+\hat{h_2}y+\hat{h_3}}{\hat{h_7}x+\hat{h_8}y+1},y' = \frac{\hat{h_4}x+\hat{h_5}y+\hat{h_6}}{\hat{h_7}x+\hat{h_8}y+1}. \tag2
x′=h7?^?x+h8?^?y+1h1?^?x+h2?^?y+h3?^??,y′=h7?^?x+h8?^?y+1h4?^?x+h5?^?y+h6?^??.(2)
分析
H
^
\hat H
H^依赖于坐标的改变。这种改变简化了公式,解揭示了重要性。【4】采取同样的技术计算单应几何误差。特别地,我们旋转初始坐标系
(
x
,
y
)
(x,y)
(x,y)建立新的坐标
(
u
,
v
)
(u,v)
(u,v)。新坐标和旧坐标有如下关系:
[
x
y
]
=
[
c
o
s
θ
?
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
[
u
v
]
,
(3)
\left[ \begin{matrix} x \\ y \end{matrix} \right] = \left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right] \left[ \begin{matrix} u \\ v \end{matrix} \right] ,\tag3
[xy?]=[cosθsinθ??sinθcosθ?][uv?],(3)
θ
=
a
t
a
n
2
(
?
h
8
^
,
?
h
7
^
)
.
(4)
\theta = atan2(-\hat{h_8},-\hat{h_7}).\tag4
θ=atan2(?h8?^?,?h7?^?).(4)
坐标改变之后,得到了新的单应矩阵
H
H
H,是
(
u
,
v
)
(u,v)
(u,v)到
(
x
′
,
y
′
)
(x',y')
(x′,y′)的映射。对应的公式变成了:
[
x
′
y
′
1
]
~
[
h
1
h
2
h
3
h
4
h
5
h
6
?
c
0
1
]
[
u
v
1
]
,
(5)
\left[ \begin{matrix} x' \\ y' \\ 1 \end{matrix} \right] \sim \left[ \begin{matrix} h_1 & h_2 & h_3\\ h_4 & h_5 & h_6 \\ -c & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right], \tag5
???x′y′1????~???h1?h4??c?h2?h5?0?h3?h6?1???????uv1????,(5)
w
h
e
r
e
[
h
1
h
2
h
4
h
5
]
=
[
h
1
^
h
2
^
h
4
^
h
5
^
]
[
c
o
s
θ
?
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
,
(6)
where\left[ \begin{matrix} h1 & h2\\ h4 & h5 \end{matrix} \right] = \left[ \begin{matrix} \hat{h_1} & \hat{h_2} \\ \hat{h_4} & \hat{h_5} \end{matrix} \right] \left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right] ,\tag6
where[h1h4?h2h5?]=[h1?^?h4?^??h2?^?h5?^??][cosθsinθ??sinθcosθ?],(6)
(
h
3
,
h
6
)
=
(
h
^
3
,
h
^
6
,
)
(7)
(h_3,h_6) = (\hat h_3,\hat h_6,\tag7)
(h3?,h6?)=(h^3?,h^6?,)(7)
c
=
h
7
2
^
+
h
8
2
^
.
(8)
c = \sqrt{\hat{h_7^2}+\hat{h_8^2}}. \tag8
c=h72?^?+h82?^??.(8)
新的映射公式也可以写成:
x
′
=
H
x
(
u
,
v
)
=
h
1
u
+
h
2
v
+
h
3
1
?
c
u
,
(9)
x' = H_x(u,v)=\frac{h_1u+h_2v+h3}{1-cu},\tag9
x′=Hx?(u,v)=1?cuh1?u+h2?v+h3?,(9)
y
′
=
H
y
(
u
,
v
)
=
h
4
u
+
h
5
v
+
h
6
1
?
c
u
.
(10)
y' = H_y(u,v)=\frac{h_4u+h_5v+h6}{1-cu}.\tag{10}
y′=Hy?(u,v)=1?cuh4?u+h5?v+h6?.(10)
映射表示为u和v的函数:
[
x
′
,
y
′
]
T
=
H
(
u
,
v
)
=
[
H
x
(
u
,
v
)
,
H
y
(
u
,
v
)
]
T
[x',y']^T = H(u,v) = [H_x(u,v),H_y(u,v)]^T
[x′,y′]T=H(u,v)=[Hx?(u,v),Hy?(u,v)]T
(没有歧义,H用于变换矩阵和映射函数。)
变换的好处是公式里 h 8 = 0 h_8=0 h8?=0。公式9和10分母中只有u,改变坐标会导致下面的事情发生:
(i) 大小改变
首先分析图片的大小是如何根据投影变换而改变的。分析依赖于矩阵分解。特别地, H H H可以被分解成一个仿射变换 H A H_A HA?和一个纯投影变换 H P H_P HP?(根据论文[3])。
[
h
1
h
2
h
3
h
4
h
5
h
6
?
c
0
1
]
?
H
=
[
h
1
+
c
h
3
h
2
h
3
h
4
+
c
h
6
h
5
h
6
0
0
1
]
?
H
A
[
1
0
0
0
1
0
?
c
0
1
]
?
H
P
.
(11)
\underbrace{\left[ \begin{matrix} h_1 & h_2 & h_3\\ h_4 & h_5 & h_6 \\ -c & 0 & 1 \end{matrix} \right]}_H = \underbrace{\left[ \begin{matrix} h_1+ch_3 & h_2 & h_3\\ h_4+ch6 & h_5 & h_6 \\ 0 & 0 & 1 \end{matrix} \right]}_{H_A}\underbrace{\left[ \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ -c & 0 & 1 \end{matrix} \right]}_{H_P}.\tag{11}
H
???h1?h4??c?h2?h5?0?h3?h6?1??????=HA?
???h1?+ch3?h4?+ch60?h2?h5?0?h3?h6?1??????HP?
???10?c?010?001??????.(11)
(
u
,
v
)
(u,v)
(u,v)的局部改变是由
(
u
,
v
)
(u,v)
(u,v)点
H
H
H的雅可比行列式决定的,
d
e
t
J
(
u
,
v
)
detJ(u,v)
detJ(u,v),它与
H
A
H_A
HA?和
H
P
H_P
HP?相关。
d
e
t
J
(
u
,
v
)
=
d
e
t
J
A
(
u
,
v
)
?
d
e
t
J
P
(
u
,
v
)
=
S
A
?
1
(
1
?
c
u
)
3
(12)
det J(u,v) = det J_A(u,v) \cdot detJ_P(u,v) = S_A \cdot \frac{1}{(1-cu)^3} \tag{12}
detJ(u,v)=detJA?(u,v)?detJP?(u,v)=SA??(1?cu)31?(12)
S
A
=
d
e
t
J
A
(
u
,
v
)
S_A = det J_A(u,v)
SA?=detJA?(u,v)是一个与u,v无关的常数。根据等式12,局部区域改变的范围因子
H
H
H只与u有关。特别地,当坐标u变大时,局部区域H变大,导致更大的区域损失。图2(b)给出了投影变换的例子,该区域损失变大沿着u轴正向。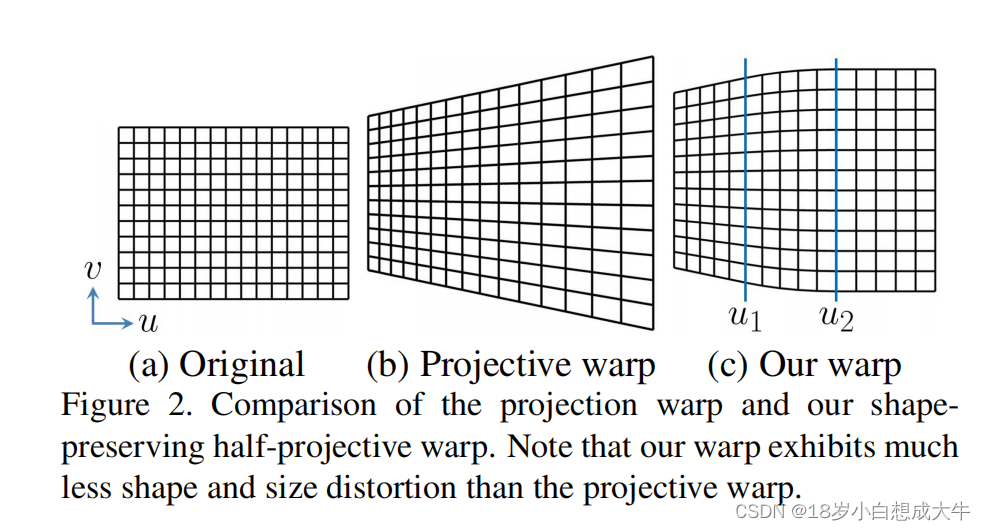
(ii) H线性化
仿射变换保护了直线的长度比,但投影变换通常不是这样的。然而,在当前条件下,坐标改变揭示了,长度比可以在投影变换时被保护。对于等式9和10,如果
u
=
u
0
u=u_0
u=u0?是一个固定值,那么
H
x
(
u
0
,
v
)
H_x(u_0,v)
Hx?(u0?,v)和
H
y
(
u
0
,
v
)
H_y(u_0,v)
Hy?(u0?,v)是关于v的线性函数:
x
′
=
H
x
(
u
0
,
v
)
=
h
2
1
?
c
u
0
v
+
h
1
u
0
+
h
3
1
?
c
u
0
,
(13)
x' = H_x(u_0,v) = \frac{h_2}{1-cu_0}v+\frac{h_1u_0+h_3}{1-cu_0},\tag{13}
x′=Hx?(u0?,v)=1?cu0?h2??v+1?cu0?h1?u0?+h3??,(13)
y
′
=
H
y
(
u
0
,
v
)
=
h
5
1
?
c
u
0
v
+
h
4
u
0
+
h
6
1
?
c
u
0
.
(14)
y' = H_y(u_0,v) = \frac{h_5}{1-cu_0}v+\frac{h_4u_0+h_6}{1-cu_0}.\tag{14}
y′=Hy?(u0?,v)=1?cu0?h5??v+1?cu0?h4?u0?+h6??.(14)
换句话说,对于与v方向平行的直线,
H
H
H保护线上的点的距离比。
(iii)平行线条曲面
有平行线条的曲面是被直线扫过的曲面。参数形式为:
s
(
u
,
v
)
=
p
(
u
)
+
v
?
r
(
u
)
\mathbf{s}(u,v) = \mathbf{p}(u)+v \cdot \mathbf{r}(u)
s(u,v)=p(u)+v?r(u),其中,
p
(
u
)
\mathbf{p}(u)
p(u)是基准曲线,
r
(
u
)
\mathbf{r}(u)
r(u)是指导曲线【5】(这里论文可能写错了,是r(u)不是r(v))。考虑到函数k的形式
k
(
u
,
v
)
=
f
(
u
)
v
+
g
(
u
)
k(u,v) = f(u)v+g(u)
k(u,v)=f(u)v+g(u),它的图曲面由
(
u
,
v
,
k
(
u
,
v
)
)
(u,v,k(u,v))
(u,v,k(u,v))三次空间构成,
[
u
v
k
(
u
,
v
)
]
=
[
u
0
g
(
u
)
]
?
p
(
u
)
+
v
[
0
1
f
(
u
)
]
?
r
(
u
)
,
(15)
\left[ \begin{matrix} u \\ v \\ k(u,v) \end{matrix} \right] = \underbrace{\left[ \begin{matrix} u \\ 0 \\ g(u) \end{matrix} \right]}_{\mathbf{p}(u)}+v\underbrace{\left[ \begin{matrix} 0 \\ 1 \\ f(u) \end{matrix} \right]}_{\mathbf{r}(u)},\tag{15}
???uvk(u,v)????=p(u)
???u0g(u)??????+vr(u)
???01f(u)??????,(15)
展示了它的平行线条曲面。虽然
H
x
(
u
,
v
)
H_x(u,v)
Hx?(u,v)和
H
y
(
u
,
v
)
H_y(u,v)
Hy?(u,v)可以写作
f
(
u
)
v
+
g
(
u
)
f(u)v+g(u)
f(u)v+g(u),它们的图是平行线条曲面。等式13和14也揭示了这一事实。等式13表明
H
x
H_x
Hx?的图和平面
u
=
u
0
u=u_0
u=u0?的相交是一条直线,说明直线沿u轴移动和旋转可以构成
H
x
H_x
Hx?的图。因此,
H
x
H_x
Hx?形成一个ruled surface。同理应用于公式14中的
H
y
H_y
Hy?。
3.2 半投影扭曲
我们的扭曲结构利用了坐标改变投影变换H的上面三种性质。首先,通过直线
u
=
u
1
u=u_1
u=u1?将空间分成两部分
R
H
=
{
(
u
,
v
)
∣
u
≤
u
1
}
R_H = \{(u,v)|u\leq u_1\}
RH?={(u,v)∣u≤u1?}和
R
L
=
{
(
u
,
v
)
∣
u
>
u
1
}
R_L = \{(u,v)|u > u_1\}
RL?={(u,v)∣u>u1?}。对于
R
H
R_H
RH?应用变换
H
H
H,对于
R
L
R_L
RL?,虽然
R
L
R_L
RL?会比
R
H
R_H
RH?造成更大的区域损失,我们提出用相似变换
S
S
S代替
H
H
H。然而变换必须连续。否则,在
R
H
R_H
RH?和
R
L
R_L
RL?的边界会有明显的接缝。为了建立连续变换,我们需要在分割线上的所有点
(
u
,
v
)
(u,v)
(u,v)都有
S
(
u
,
v
)
=
H
(
u
,
v
)
S(u,v)=H(u,v)
S(u,v)=H(u,v)。注意:这种需求并不满足任意一个分割线,因为投影变换在直线的生成上不是线性变换,但相似变换是。幸运地是,感谢性质(ii),通过选择和v轴平行的直线
u
=
u
1
u=u_1
u=u1?,可以达到连续的需求,因为
H
(
u
1
,
v
)
H(u_1,v)
H(u1?,v)对于v是一个线性函数,通过对于所有v的要求
S
(
u
,
v
)
=
H
(
u
,
v
)
S(u,v)=H(u,v)
S(u,v)=H(u,v),
S
S
S被唯一确定为:
s
(
u
,
v
)
=
1
1
?
c
u
1
(
[
h
5
h
2
?
h
2
h
5
]
[
u
v
]
+
[
(
h
1
?
h
5
)
u
1
+
h
3
(
h
4
+
h
2
)
u
1
+
h
6
]
)
(16)
s(u,v) = \frac{1}{1-cu_1}\bigg(\left[ \begin{matrix} h_5 & h_2\\ -h_2 & h_5 \end{matrix} \right] \left[ \begin{matrix} u \\ v \end{matrix} \right] +\left[ \begin{matrix} (h_1 - h_5)u_1 + h_3\\ (h_4 + h_2)u_1 + h_6 \end{matrix} \right]\bigg) \tag{16}
s(u,v)=1?cu1?1?([h5??h2??h2?h5??][uv?]+[(h1??h5?)u1?+h3?(h4?+h2?)u1?+h6??])(16)
u
1
u_1
u1?是变换参数,第四单元讨论。

图3举了一个例子,a展示了从投影变换
H
^
\hat H
H^中计算转后后的uv坐标系。c展示了使用上述方法半投影变换的连续结构。结构给出了一个变换函数是连续的
C
0
C^0
C0,半投影和半相似变换。和b展示的单一投影变换相比,我们的变换有更少的形状和区域损失。然而,它在
u
=
u
1
u=u_1
u=u1?有一个突然的直线弯曲。更具体的是,
R
H
R_H
RH?或
R
L
R_L
RL?内的线是直线,通过
u
=
u
1
u=u_1
u=u1?的线会被弯曲。为了减少这种情况,我们引入一个缓冲区域取代在
R
L
R_L
RL?中使用单一线性变换。缓冲区域是在H光滑外推的位置,以至于
R
L
R_L
RL?中的变换函数是连续可微的(
C
1
C^1
C1),并且从H到相似变换S是渐变的。
3.1 C 1 C^1 C1外推
为了构建
C
1
C^1
C1扭曲,我们提出一个上述方法的推论。通过将
R
L
R_L
RL?划分成两个部分
R
T
=
{
(
u
,
v
)
∣
u
1
<
u
<
u
2
}
R_T=\{(u,v)|u_1<u<u_2\}
RT?={(u,v)∣u1?<u<u2?}和
R
S
=
{
(
u
,
v
)
∣
u
2
≤
u
}
R_S=\{(u,v)|u_2\leq u\}
RS?={(u,v)∣u2?≤u},展示在图2的c中。
u
1
u_1
u1?和
u
2
u_2
u2?是扭曲函数的两个参数,在第四单元被定义。扭曲函数定义为:
w
(
u
,
v
)
=
{
H
(
u
,
v
)
i
f
(
u
,
v
)
∈
R
H
T
(
u
,
v
)
i
f
(
u
,
v
)
∈
R
T
S
(
u
,
v
)
i
f
(
u
,
v
)
∈
R
S
.
(17)
w(u,v) = \begin{cases} H(u,v) & if(u,v)\in R_H \\ T(u,v) & if(u,v)\in R_T \\ S(u,v) & if(u,v)\in R_S \\ \end{cases}.\tag{17}
w(u,v)=??????H(u,v)T(u,v)S(u,v)?if(u,v)∈RH?if(u,v)∈RT?if(u,v)∈RS??.(17)
T
(
u
,
v
)
T(u,v)
T(u,v)是定义在中间区域
R
T
R_T
RT?的函数,它是一个从
H
(
u
,
v
)
H(u,v)
H(u,v)到
S
(
u
,
v
)
S(u,v)
S(u,v)逐渐变换的函数。
S
(
u
,
v
)
S(u,v)
S(u,v)是一个定义在
R
S
R_S
RS?的相似变换。通过下面式子将相似变换用参数表示:
s
(
u
,
v
)
=
[
S
x
(
u
,
v
)
S
y
(
u
,
v
)
]
=
[
α
?
β
β
α
]
[
u
v
]
+
[
t
x
t
y
]
.
(18)
s(u,v) = \left[\begin{matrix} S_x(u,v) \\ S_y(u,v) \end{matrix} \right] = \left[ \begin{matrix} \alpha & -\beta \\ \beta & \alpha \end{matrix} \right]\left[ \begin{matrix} u \\ v \end{matrix} \right]+\left[ \begin{matrix} t_x \\ t_y \end{matrix} \right].\tag{18}
s(u,v)=[Sx?(u,v)Sy?(u,v)?]=[αβ??βα?][uv?]+[tx?ty??].(18)
给定一个投影变换H,首先确定
u
1
u_1
u1?和
u
2
u_2
u2?,然后建立一个变换w(公式17)。
根据3.2中的性质(iii),我们已经了解
H
x
H_x
Hx?和
H
y
H_y
Hy?表示两个直纹曲面图。从公式18中可知,
S
x
S_x
Sx?和
S
y
S_y
Sy?也是在3D空间中也是直纹平面。这激发我们去追求
T
x
(
u
,
v
)
T_x(u,v)
Tx?(u,v)和
T
y
(
u
,
v
)
T_y(u,v)
Ty?(u,v)也是直纹曲面图。因此,我们假设
T
(
u
,
v
)
T(u,v)
T(u,v)等于如下式子:
T
(
u
,
v
)
=
[
T
x
(
u
,
v
)
T
y
(
u
,
v
)
]
=
[
f
x
(
u
)
f
y
(
u
)
]
v
+
[
g
x
(
u
)
g
y
(
u
)
]
.
(19)
T(u,v) = \left[ \begin{matrix} T_x(u,v) \\ T_y(u,v) \end{matrix} \right]=\left[ \begin{matrix} f_x(u) \\ f_y(u) \end{matrix} \right]v+\left[ \begin{matrix} g_x(u) \\ g_y(u) \end{matrix} \right].\tag{19}
T(u,v)=[Tx?(u,v)Ty?(u,v)?]=[fx?(u)fy?(u)?]v+[gx?(u)gy?(u)?].(19)
为了建立变换w,我们需要确定参数
α
,
β
,
t
x
,
t
y
\alpha,\beta,t_x,t_y
α,β,tx?,ty?
,为了相似变换S和T的四个函数
f
x
,
f
y
,
g
x
,
g
y
f_x,f_y,g_x,g_y
fx?,fy?,gx?,gy?。我们假设四个函数是u的多项式函数。把公式9,10,18,19带入到公式17,变换函数w可以用如下式子表示:
w
(
u
,
v
)
=
[
w
x
(
u
,
v
)
w
y
(
u
,
v
)
]
=
[
F
x
(
u
)
v
+
G
x
(
u
)
F
y
(
u
)
v
+
G
y
(
u
)
]
,
(20)
w(u,v) = \left[ \begin{matrix} w_x(u,v) \\ w_y(u,v) \end{matrix} \right]=\left[ \begin{matrix} F_x(u)v+G_x(u) \\ F_y(u)v+G_y(u) \end{matrix} \right],\tag{20}
w(u,v)=[wx?(u,v)wy?(u,v)?]=[Fx?(u)v+Gx?(u)Fy?(u)v+Gy?(u)?],(20)
where
F
x
(
u
)
=
{
h
2
1
?
c
u
i
f
?
u
≤
u
1
f
x
(
u
)
i
f
?
u
1
<
u
<
u
2
?
β
i
f
?
u
2
≤
u
,
(21)
F_x(u) = \begin{cases} \frac{h_2}{1-cu} & if \ u \leq u1 \\ f_x(u) & if \ u_1< u < u_2\\ -\beta & if \ u_2 \leq u \\ \end{cases},\tag{21}
Fx?(u)=??????1?cuh2??fx?(u)?β?if?u≤u1if?u1?<u<u2?if?u2?≤u?,(21)
G
x
(
u
)
=
{
h
1
u
+
h
3
1
?
c
u
i
f
?
u
≤
u
1
g
x
(
u
)
i
f
?
u
1
<
u
<
u
2
α
u
+
t
x
i
f
?
u
2
≤
u
.
(22)
G_x(u) = \begin{cases} \frac{h_1u+h_3}{1-cu} & if \ u \leq u1 \\ g_x(u) & if \ u_1< u < u_2\\ \alpha u+t_x & if \ u_2 \leq u \\ \end{cases}.\tag{22}
Gx?(u)=??????1?cuh1?u+h3??gx?(u)αu+tx??if?u≤u1if?u1?<u<u2?if?u2?≤u?.(22)
F
y
F_y
Fy?和
G
y
G_y
Gy?可以类似表示。
剩下的问题就是找到合适的
f
x
,
f
y
,
g
x
,
g
y
,
α
,
β
,
t
x
,
t
y
f_x,f_y,g_x,g_y,\alpha,\beta,t_x,t_y
fx?,fy?,gx?,gy?,α,β,tx?,ty?来保证w是
C
1
C^1
C1连续函数。那么就要求
F
x
,
G
x
,
F
y
,
G
y
F_x,G_x,F_y,G_y
Fx?,Gx?,Fy?,Gy?都是
C
1
C^1
C1连续。以
F
x
F_x
Fx?为例,根据等式21,
F
x
F_x
Fx?是
C
1
C^1
C1如果满足以下四条:
f
x
(
u
1
)
=
h
2
1
?
c
u
1
?
(
F
x
(
u
1
)
?
i
s
?
c
o
n
t
i
n
u
o
u
s
)
(23)
f_x(u_1)=\frac{h_2}{1-cu_1} \ (F_x(u_1) \ is \ continuous) \tag{23}
fx?(u1?)=1?cu1?h2???(Fx?(u1?)?is?continuous)(23)
f
x
′
(
u
1
)
=
c
h
2
(
1
?
c
u
1
)
2
?
(
F
x
′
(
u
1
)
?
i
s
?
c
o
n
t
i
n
u
o
u
s
)
(24)
f'_x(u_1)=\frac{ch_2}{(1-cu_1)^2} \ (F'_x(u_1) \ is \ continuous) \tag{24}
fx′?(u1?)=(1?cu1?)2ch2???(Fx′?(u1?)?is?continuous)(24)
f
x
(
u
2
)
=
?
β
?
(
F
x
(
u
2
)
?
i
s
?
c
o
n
t
i
n
u
o
u
s
)
(25)
f_x(u_2)=-\beta \ (F_x(u_2) \ is \ continuous) \tag{25}
fx?(u2?)=?β?(Fx?(u2?)?is?continuous)(25)
f
x
′
(
u
2
)
=
0
?
(
F
x
′
(
u
2
)
?
i
s
?
c
o
n
t
i
n
u
o
u
s
)
(26)
f'_x(u_2)=0 \ (F'_x(u_2) \ is \ continuous) \tag{26}
fx′?(u2?)=0?(Fx′?(u2?)?is?continuous)(26)
因为我们有四个线性约束,我们可以有最多四个参数。因为
β
\beta
β已经是一个参数,
f
x
f_x
fx?可以有三个参数。因此,我们假设
f
x
f_x
fx?是一个关于u的二次函数,通过解4×4线性方程组,可以获得
f
x
(
u
)
f_x(u)
fx?(u)和
β
\beta
β。类似
f
y
(
u
)
f_y(u)
fy?(u)和
α
\alpha
α可以通过
F
y
F_y
Fy?的
C
1
C^1
C1来求解。用相同的策略在
G
x
G_x
Gx?上得到
g
x
(
u
)
g_x(u)
gx?(u)和
t
x
t_x
tx?。最后,通过
G
y
G_y
Gy?得到
g
y
(
u
)
g_y(u)
gy?(u)和
t
y
t_y
ty?。
总之,扭曲变换外推
H
(
u
,
v
)
H(u,v)
H(u,v)到
R
T
R_T
RT?和
R
S
R_S
RS?通过自动确定函数
T
(
u
,
v
)
T(u,v)
T(u,v)和
S
(
u
,
v
)
S(u,v)
S(u,v)。概率来说,给出两个图片的投影变换
H
^
\hat H
H^,我们建立扭曲函数w是
C
1
C^1
C1连续的,在一个半空间投影,在另一个半连续变成相似变换。图3d展示了这种结构扭曲。下个单元讨论如何应用该变换去拼接图片和如何确定参数
u
1
,
u
2
u_1,u_2
u1?,u2?。
4.图像拼接
这个单元展示如何使用提出的扭曲方法去拼接图片。首先描述如何应用在双图拼接和如何自动确定参数u1和u2。然后,我们提出一个新的结合APAP的扭曲策略去加强二者。
4.1 形变保护的图像拼接
给定两张图片
I
1
,
I
2
I_1,I_2
I1?,I2?,假设它们之间的单应矩阵
H
12
H_{12}
H12?是
I
2
I_2
I2?中的点
(
x
2
,
y
2
)
(x_2,y_2)
(x2?,y2?)到
I
1
I_1
I1?中的点
(
x
1
,
y
1
)
(x_1,y_1)
(x1?,y1?)的映射。如下图所示:
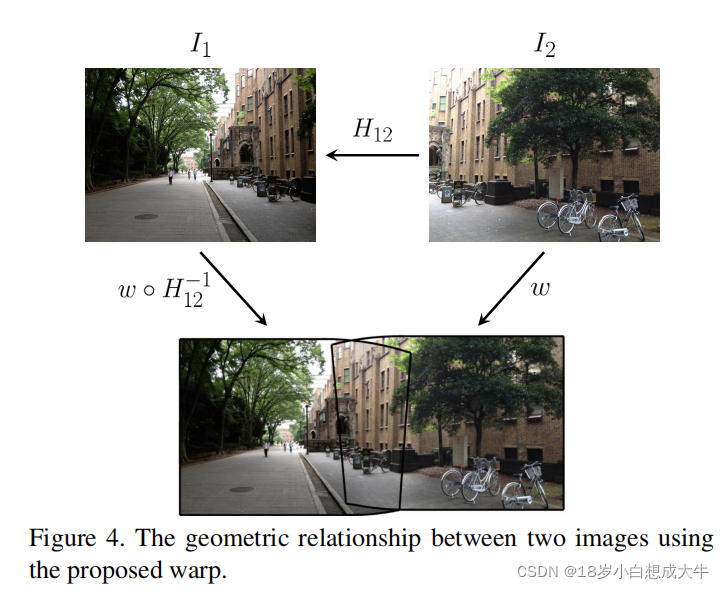
如果
I
2
I_2
I2?通过w扭曲,
I
1
I_1
I1?应该通过
w
°
H
12
?
1
w \circ H_{12}^{-1}
w°H12?1?扭曲,为了维持
H
12
H_{12}
H12?中描述的几何相关性。当
w
=
H
12
w=H_{12}
w=H12?时,就是图2到固定图1的单应。当
w
=
I
w=I
w=I时,图2是固定的,图1通过
H
12
?
1
H_{12}^{-1}
H12?1?扭曲。我们从
H
12
H_{12}
H12?中得到第3部分描述的扭曲变换,使用它作为w拼接两幅图,如图4。
接下来介绍如何确定参数u1和u2。虽然扭曲的目标是获得每张图片的透视变换,我们也想尽可能知道每张图片进行怎养的相似变换。因此,我们想让结构化的扭曲w接近相似变换。为了实现它,我们把每张图片和能量E联系起来,E衡量扭曲函数w来自最近相似变换在Frobenius范数的偏差。
注:矩阵的F范数定义为矩阵各元素的绝对值平方的总和开根号,类比向量的L2范数。
E
i
(
u
1
,
u
2
)
=
m
i
n
a
i
,
b
i
?
(
x
,
y
)
∈
Ω
i
∣
∣
J
i
(
x
,
y
;
u
1
,
u
2
)
?
[
a
i
?
b
i
b
i
a
i
]
∣
∣
F
2
d
x
d
y
(27)
E_i(u_1,u_2) = \underset{a_i,b_i}{min} \iint_{(x,y)\in \Omega_i} \bigg\lvert\bigg\lvert J_ i(x,y;u_1,u_2)-\left[ \begin{matrix} a_i & -b_i \\ b_i & a_i \end{matrix} \right]\bigg\lvert\bigg\lvert_F^2 dxdy \tag{27}
Ei?(u1?,u2?)=ai?,bi?min??(x,y)∈Ωi??∣∣∣∣?∣∣∣∣?Ji?(x,y;u1?,u2?)?[ai?bi???bi?ai??]∣∣∣∣?∣∣∣∣?F2?dxdy(27)
Ω
i
\Omega_i
Ωi?是
I
i
I_i
Ii?的矩形域。
J
i
(
x
,
y
;
u
1
,
u
2
)
J_ i(x,y;u_1,u_2)
Ji?(x,y;u1?,u2?)是wi评估点(x,y)的雅可比矩阵。因为u1,u2是wi的参数,雅可比行列式依赖(u1,u2)。拼接两张图的例子中,总的能量
E
(
u
1
,
u
2
)
=
E
1
(
u
1
,
u
2
)
+
E
2
(
u
1
,
u
2
)
E(u_1,u_2) = E_1(u_1,u_2)+E_2(u_1,u_2)
E(u1?,u2?)=E1?(u1?,u2?)+E2?(u1?,u2?),
w
1
=
w
°
H
12
?
1
w_1 = w \circ H_{12}^{-1}
w1?=w°H12?1?并且
w
2
=
w
w_2 = w
w2?=w(w是来自H12的变换)。注意:虽然最小化Ei可能导致相似变换,它们的连接最优有一个好的折中在拼接需求和相似需求之间。能量是u1和u2的非线性函数。通过在参数空间(u1,u2)中有规律的抽样优化,评估能量在抽样位置和选择最低能量。
为了多图拼接,我们执行一组拼接方式一次同时拼接所有的输入图片。我们的方式找到每对相邻图片的单应矩阵
H
i
,
i
+
1
H_{i,i+1}
Hi,i+1?和第一张图片和最后一张图片的单应矩阵
H
1
n
H_{1n}
H1n?。
H
1
n
H_{1n}
H1n?用于获得变换w。
I
n
I_n
In?通过w变换,并且每张其他的图片
I
i
I_i
Ii?通过
w
°
H
1
n
?
1
w\circ H_{1n}^{-1}
w°H1n?1?得到变换。下图展示了三张图片同时拼接。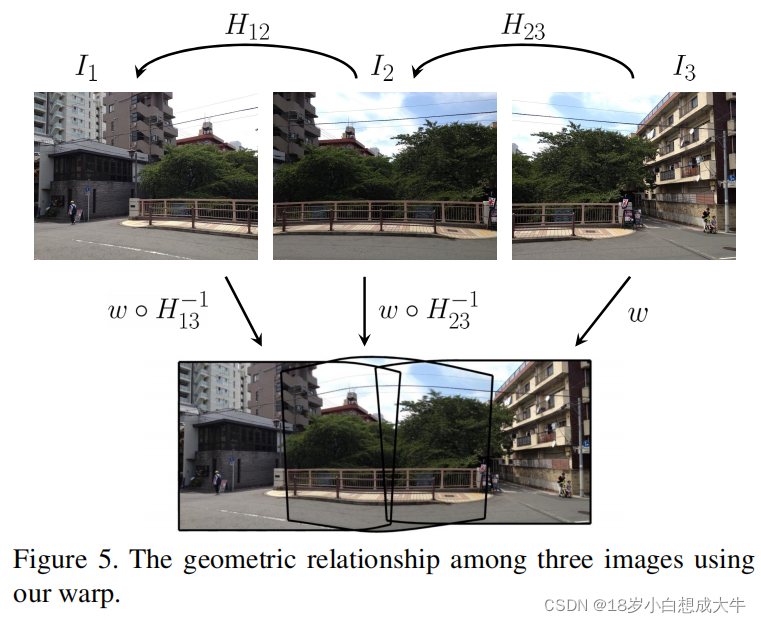
4.2 和APAP结合
本文提出的方法更关注保护透视变换,而不是拼接准确。然而,它可以和有更好拼接准确度的方法结合达到透视保护和准确度都增强的目的。APAP是配准的顶级算法。和APAP结合的可能方式是用本文提出的半投影扭曲取代移动DLT中的投影扭曲。然而,需要确定空间变量(u1,u2),该变量是不易求且不直观的。下面我们用一个简单的策略结合APAP和SPHP。
分为两个过程:投影变换H,然后扭曲
w
°
H
?
1
w \circ H^{-1}
w°H?1。如下图a所示。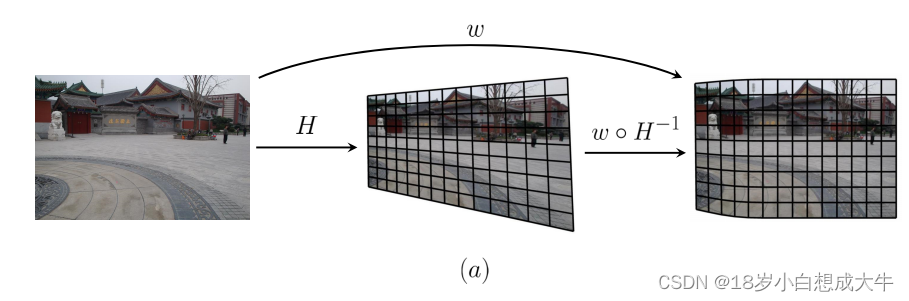
这种扭曲可以看作降低投影损失的方式。具体地,只在
R
L
R_L
RL?大的区域扭曲,
R
H
R_H
RH?小的区域不动。虽然APAP是一个局部变量扭曲,它也是一个全局投影变换。因此,我们可以把它视作一个投影扭曲并应用我们的扭曲方式去降低损失。如下图b所示。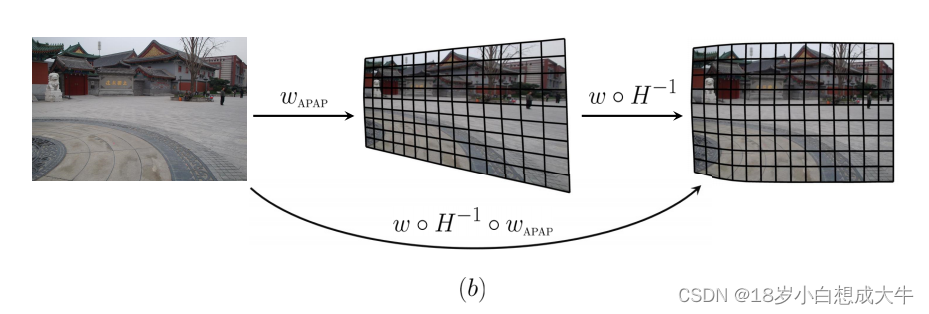
这样,当全局形状通过我们的方法调整时,图片通过APAP局部配准。总之,结合APAP的扭曲函数定义为:
w
°
H
?
1
°
w
A
P
A
P
.
(28)
w \circ H^{-1} \circ w_{APAP}. \tag{28}
w°H?1°wAPAP?.(28)
下图展示了更新的几何关系当采用了结合APAP的方法后。
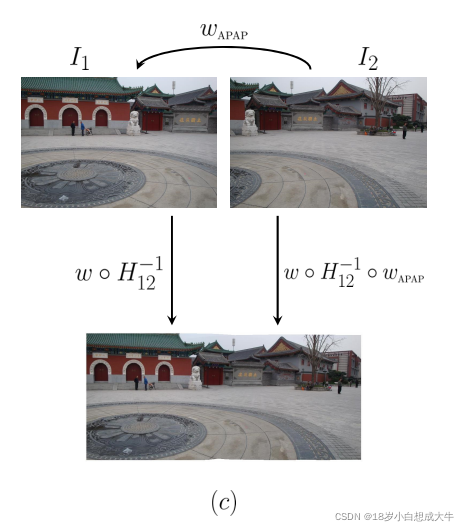
5.实验
和自动拼接比较。自动拼接假设输入图片都共享相同的相机中心和使用一个3D选择模型。对于投影扭曲和我们的扭曲方法,使用VLFeat库去提取SIFT特征,通过RANSAC匹配特征点,获取重叠区域的投影变换。固定一张图作为参照图,对另一张图使用投影变换拼接。我们手动选择参考图为了最好结果损失少的投影变换。在得到投影变换后,确定参数u1和u2,结构化扭曲,然后用扭曲函数去配准图像。配准图像用线性融合处理。
MATLAB代码,输入图片分辨率800×600,5秒找到参数u1和u2,不到两秒完成扭曲结构和图片扭曲结合。下图比较了投影变换,自动拼接,和SPHP。
投影变换大小、形状等损失很大,自动拼接降低了区域损失,但是有些重要的直线弯曲了。SPHP减少了投影损失,保护每张图的透视变换。因为投影和相似变换不包括直线损失,SPHP仅在
R
T
R_T
RT?中有直线损失。下图比较了这三种方式拼接10张图的效果。
自动拼接形变严重。投影变换区域和形状损失都严重。SPHP损失少,而且视野更广。
下图比较APAP和SPHP+APAP在两张图的拼接效果。
SPHP用之前的图?展示的方式。因此,SPHP可以保持APAP的配准程度,当调整结果的全部形状为了降低损失。这些例子不能很好配准,通过单一投影变换。结合APAP之后,SPHP方法更鲁棒。
6.结论
本文提出一个新的图像拼接方法。我们的方法全局配准图片,保护了原始的透视关系。结合了APAP后,配准更准确,损失更少,视野更广。参数选择目前没用考虑图片内容(如线性特征)。因此,当场景中充满线性结构,参数对降低线性损失是无效的。未来,我们将探索更多的可能,将我们的方法应用在不同地方,比如场景变形。