本系列博客包括6个专栏,分别为:《自动驾驶技术概览》、《自动驾驶汽车平台技术基础》、《自动驾驶汽车定位技术》、《自动驾驶汽车环境感知》、《自动驾驶汽车决策与控制》、《自动驾驶系统设计及应用》,笔者不是自动驾驶领域的专家,只是一个在探索自动驾驶路上的小白,此系列丛书尚未阅读完,也是边阅读边总结边思考,欢迎各位小伙伴,各位大牛们在评论区给出建议,帮笔者这个小白挑出错误,谢谢!
此专栏是关于《自动驾驶汽车环境感知》书籍的笔记
3.卷积神经网络概念及性质
3.1 概述
使用全连接前馈网络处理图像的两个问题:
- 参数量巨大:假如输入图像像素为1000×1000像素,在全连接前馈网络中,第一个隐藏层的每个神经元到输入层都有1000000个相互独立的连接,对应1000000个权重参数;如果处理的是RGB彩色图,则有3000000个参数;如果要得到更好的效果,再加几个隐藏层,参数规模会继续翻倍增加;
- 局部不变性特征:自然图像中的物体具有局部不变性特征,如:尺度缩放、平移、旋转等操作不影响其语义信息;全连接前馈网络很难提取这些局部不变特征,一般需要数据增强来提高性能;
卷积神经网络介绍:
- 卷积神经网络(Convolutional Neural Network,CNN)是一种具有稀疏连接、权值共享等特征的深层前馈神经网络;
- 卷积神经网络是受生物学上感受野(receptive field)的机制提出;感受野主要指听觉、视觉等神经系统中一些神经元的特性,即神经元只接收其所支配的刺激区域内的信号;
- LeCun在1989年将方向传播算法引入神经网络,发明了卷积神经网络;
- 如今卷积神经网络一般是由卷积层、池化层和全连接层交叉叠加而成的前馈神经网络,使用反向传播算法进行训练;
- 卷积神经网络有三个结构的特性:稀疏连接、权值共享和旋转不变性;
- 卷积神经网络最擅长处理图像和视频数据,如:图像分类、人脸识别、物体识别、图像分割、物体检测等;
3.2 卷积的概念
- 点积。
点积的两种定义方式:代数方式和几何方式。- 代数定义:对于二维空间内的两个向量
u
,
v
∈
R
n
u,v\in{R^n}
u,v∈Rn,其中
u
=
[
u
1
,
u
2
,
.
.
.
,
u
n
]
,
v
=
[
v
1
,
v
2
,
.
.
.
,
v
n
]
u=[u_1,u_2,...,u_n],v=[v_1,v_2,...,v_n]
u=[u1?,u2?,...,un?],v=[v1?,v2?,...,vn?],
u
u
u和
v
v
v的点积定义:
u ? v = ∑ i = 1 n u i v i = u 1 v 1 + u 2 v 2 + . . . + u n v n u·v=\sum^n_{i=1}u_iv_i=u_1v_1+u_2v_2+...+u_nv_n u?v=i=1∑n?ui?vi?=u1?v1?+u2?v2?+...+un?vn? - 几何定义:对于二维空间内的两个向量
u
,
v
∈
R
n
u,v\in{R^n}
u,v∈Rn,其大小分别表示为
∣
u
∣
,
∣
v
∣
|u|,|v|
∣u∣,∣v∣,它们的夹角为
θ
(
0
≤
θ
≤
π
)
\theta(0≤\theta≤\pi)
θ(0≤θ≤π),
u
u
u和
v
v
v的点积定义:
u ? v = ∣ u ∣ ∣ v ∣ cos ? θ u·v=|u||v|\cos\theta u?v=∣u∣∣v∣cosθ
理解:一个向量 u u u在另一个向量 v v v方向上的分量的长度和 v v v的长度相乘得到的值;其中, u u u在 v v v上的分量的长度称为 u u u在 v v v上的投影;
- 代数定义:对于二维空间内的两个向量
u
,
v
∈
R
n
u,v\in{R^n}
u,v∈Rn,其中
u
=
[
u
1
,
u
2
,
.
.
.
,
u
n
]
,
v
=
[
v
1
,
v
2
,
.
.
.
,
v
n
]
u=[u_1,u_2,...,u_n],v=[v_1,v_2,...,v_n]
u=[u1?,u2?,...,un?],v=[v1?,v2?,...,vn?],
u
u
u和
v
v
v的点积定义:
- 卷积。
- 一维卷积。
假设一个信号发生器每个时刻 t t t产生一个信号 x t x_t xt?,其信息衰减率为 f k f_k fk?,即在 k ? 1 k-1 k?1个时间步长后,信息为原来的 f k f_k fk?倍;假设 f 1 = 1 , f 2 = 1 / 2 , f 3 = 1 / 4 f_1=1,f_2=1/2,f_3=1/4 f1?=1,f2?=1/2,f3?=1/4,那么在时刻 t t t收到的信号 y t y_t yt?为当前时刻产生的信息和以前时刻延迟信息的叠加:
y t = 1 × x t + 1 / 2 × x t ? 1 + 1 / 4 × x t ? 2 = f 1 × x t + f 2 × x t ? 1 + f 3 × x t ? 2 = ∑ k = 1 3 f k ? x t ? k + 1 y_t=1\times{x_t}+1/2\times{x_{t-1}}+1/4\times{x_{t-2}}=f_1\times{x_t}+f_2\times{x_{t-1}}+f_3\times{x_{t-2}}=\sum^3_{k=1}f_k·x_{t-k+1} yt?=1×xt?+1/2×xt?1?+1/4×xt?2?=f1?×xt?+f2?×xt?1?+f3?×xt?2?=k=1∑3?fk??xt?k+1?
f 1 , f 2 , f 3 , . . . f_1,f_2,f_3,... f1?,f2?,f3?,...称为滤波器(filter),深度学习中称为卷积核(convolution kernel);
假设卷积核 W = [ w 1 , w 2 , . . . , w m ] W=[w_1,w_2,...,w_m] W=[w1?,w2?,...,wm?]大小为 m m m,和一个信号序列 X = [ x 1 , x 2 , . . . , x n ] X=[x_1,x_2,...,x_n] X=[x1?,x2?,...,xn?]的卷积记为: Y = W ? X , 其 中 : y t = ∑ k = 1 m w k ? x n ? k + 1 , ? 表 示 卷 积 运 算 Y=W\ast{X},其中:y_t=\sum^m_{k=1}w_k\cdot{x_{n-k+1}},\ast表示卷积运算 Y=W?X,其中:yt?=k=1∑m?wk??xn?k+1?,?表示卷积运算
一般来说,卷积核大小 m m m远小于信号序列长度 n n n;
一维卷积实例:
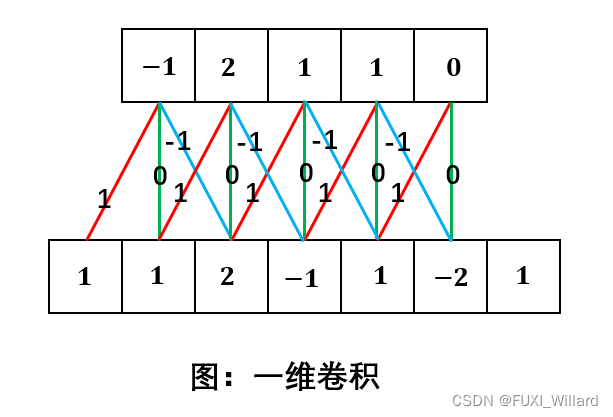
注:下面序列为输入,连接边上的数字为权重,即卷积核为 [ 1 , 0 , ? 1 ] [1,0,-1] [1,0,?1],上面序列为输出;
连续型卷积,设 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)是两个可积函数,其卷积定义为
( f ? g ) ( n ) = ∫ ? ∞ ∞ f ( τ ) g ( n ? τ ) d τ (f\ast{g})(n)=\int^{\infty}_{-\infty}f(\tau)g(n-\tau)d\tau (f?g)(n)=∫?∞∞?f(τ)g(n?τ)dτ - 二维卷积.
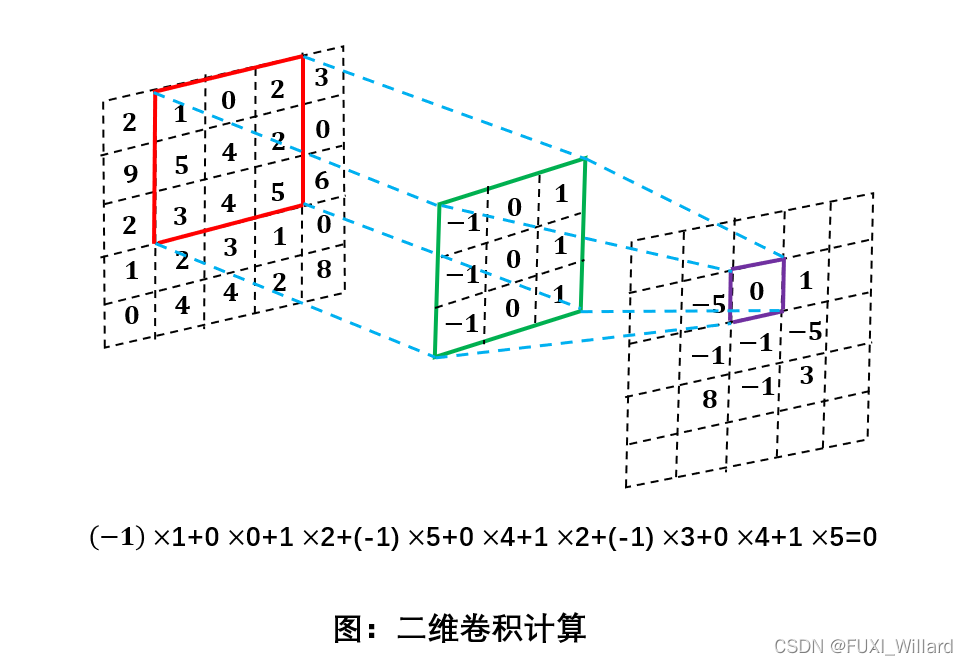
给定一个图像 X ∈ R M × N X\in{R^{M\times{N}}} X∈RM×N和卷积核 W ∈ R m × n W\in{R^{m\times{n}}} W∈Rm×n,其卷积为:
y i j = ∑ u = 1 m ∑ v = 1 n w u v ? x i ? u + 1 , j ? v + 1 y_{ij}=\sum^m_{u=1}\sum^n_{v=1}w_{uv}\cdot{x_{i-u+1,j-v+1}} yij?=u=1∑m?v=1∑n?wuv??xi?u+1,j?v+1?
卷积操作即对输入函数的每一个位置进行加权累加,卷积核就是对应输入函数在每个位置上的权重向量(一维)或权重矩阵(二维);
- 一维卷积。
- 卷积和互相关。
- 进行卷积操作时,要把卷积核翻转,在不同位置和相同大小的区域做点积;
- 互相关(cross-correlation)是一个衡量两个序列相关性的函数,通常用滑动窗口的点积计算实现;
- 给定一个图像
X
∈
R
M
×
N
X\in{R^{M\times{N}}}
X∈RM×N和卷积核
W
∈
R
m
×
n
W\in{R^{m\times{n}}}
W∈Rm×n,其互相关为:
y i j = ∑ u = 1 m ∑ v = 1 n w u v ? x i + u ? 1 , j + v ? 1 y_{ij}=\sum^m_{u=1}\sum^n_{v=1}w_{uv}\cdot{x_{i+u-1,j+v-1}} yij?=u=1∑m?v=1∑n?wuv??xi+u?1,j+v?1? - 卷积和互相关的区别在于卷积核是否翻转;在神经网络中,卷积作用是特征提取,卷积核是否翻转并没有什么影响;
- 互相关操作使用符号 ? \otimes ?表示,卷积公式表述: Y = W ? X Y=W\otimes{X} Y=W?X;
- 卷积的应用。
- 权值共享。
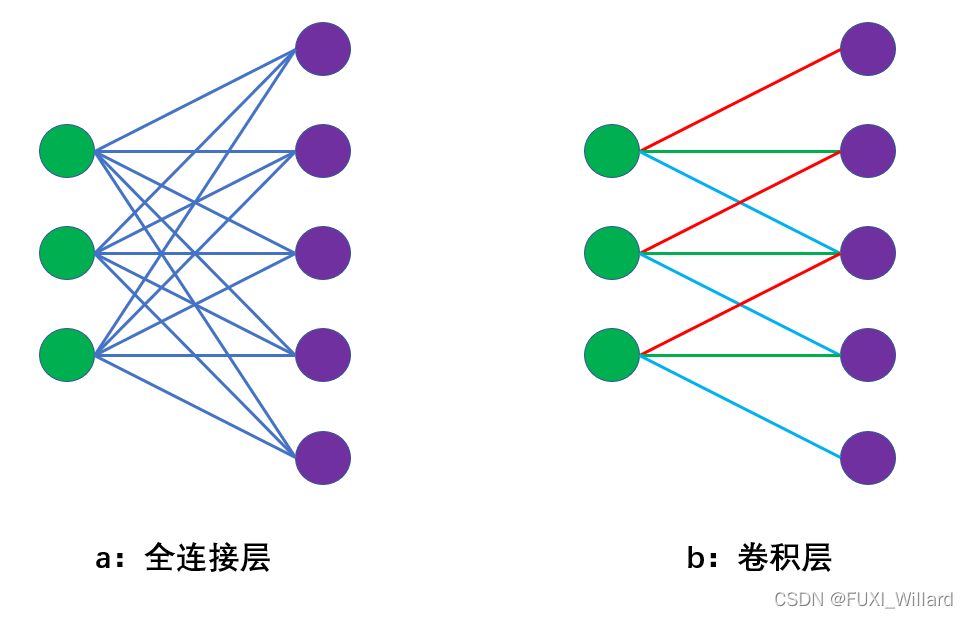
对一张图像进行卷积时,卷积核将逐一滑过图像的每个像素,即在同一个卷积操作过程中,对于不同的区域,共享同一个卷积核,参数量是卷积核大小;卷积核用来检测特征的,由于参数共享,即使图像进行一定的平移操作,一样可以识别出特征,称为"平移不变性"; - 稀疏连接。
数字图像处理领域,图像是相对连续的,局部信息的组合构成各种线条形状;一般来说,每一个像素点在空间上和周围的像素点是紧密联系的,但和远的像素点关联性较小;假如在卷积层的第 l l l层,每一个神经元都和第 l ? 1 l-1 l?1层的所有神经元相连,构成一个全连接网络,则两层间的连接数为 n ( l ) × n ( l ? 1 ) n^{(l)}\times{n^{(l-1)}} n(l)×n(l?1);若使用稀疏连接方式,构造一个 m × m m\times{m} m×m( m m m一般为3或5)的卷积核对输入层进行卷积操作,则第 l l l层每个神经元都只和卷积核内单元相连,构成一个局部连接网络,连接数为 n ( l ) × m n^{(l)}\times{m} n(l)×m。
- 多核卷积。
每个卷积核是一个特征提取器,如使用Sobel算子提取图像边缘,若只有一个卷积核,只能提取一种特征,使用多个卷积核,以多核卷积从不同角度最大限度提取图像特征;每个卷积核相应生成一幅特征图,即图像经过卷积后的不同通道(channel),多核卷积称为多通道卷积;
- 权值共享。