学习方法
- 不要死啃书,看不懂就先放弃,回过头再来看
- 去网上找相关章节的文章,归类查看并做好笔记
- 不要想着了解每个函数、参数的作用,不会不了解就去查资料即可,先上手跑起来
1、机器学习算法的整体使用步骤如下:
(1)从scikitlearn库中调用相应的机器学习算法模块;
(2)输入相应的算法参数定义一个新的算法;
(3)输入基础训练数据集利用scaler对其进行数据归一化处理
(4)对于归一化的数据集进行机器学习算法的训练fit过程;
(5)输入测试数据集对其结果进行预测predict;
(6)将预测结果与真实结果进行对比,输出其算法的准确率score(或者混淆矩阵)
专业英语
feature 特征值(除标签列以外的每一列)
target 标签/结果(一般为最后一列)
coef_ 权重系数(斜率)
intercept_ 截距
1.线性回归
regression 回归
metrics 度量(用于评估)
accuracy_score 准确率
sklearn api
https://www.cnblogs.com/Yanjy-OnlyOne/p/11288098.html
import numpy as np
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=10)
sklearn 技巧
数据
1.问题: 使用sklearn建立模型之后进行预测时出现:Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
2.原因:这是由于在新版的sklearn中,所有的数据都应该是二维矩阵。
3.解决办法:如果传入的是一个一维矩阵,直接使用.reshape(-1,1)转化为二维矩阵,如果只是一个样本数据,需要先使用numpy转化为一个一维数组,再使用reshape转化为二维数组。
常用函数 fit(),predict()
方法一:reshape
x=[1] # 一维list
np.array(x).reshape(-1,1) # array([[1]]) 二维矩阵
# np.array() 先转化为矩阵
x=[[1],[2]] # 二维list
np.array(x)
'''
array([[1],
[2]])
'''
方法二:np.newaxis
np.newaxis作用
对于[: , np.newaxis] 和 [np.newaxis,:],是在np.newaxis这里增加1维。
这样改变维度的作用往往是将一维的数据转变成一个矩阵
a=np.array([1,2,3,4,5])
aa=a[:,np.newaxis]
print(aa.shape)
print(aa)
输出:(5, 1)
[[1]
[2]
[3]
[4]
[5]]
Expected 2D array, got 1D array instead:
是因为在最新版本的sklearn中,所有的数据都应该是二维矩阵,哪怕它只是单独一行或一列。
解决:添加.reshape(-1,1)即可
model.fit(x_train.reshape(-1,1),y_train)
Expected 2D array, got scalar array instead…Reshape your data…
predict(21.079) =>
新版本
predict([[21.079]])
读取
numpy 读取
data = np.genfromtxt("job.csv", delimiter=",") # 只能读取数字 读取文字时会变成 nan
x_data = data[1:,1]
type(x_data) # numpy.ndarray
x_data # array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
pandas 读取
data=pd.read_csv('input_data.csv')
x=data['square_feet']
y=data['price']
type(x) # pandas.core.series.Series
y
'''
0 6450
1 7450
2 8450
3 9450
4 11450
5 15450
6 18450
Name: price, dtype: int64
'''
np.array(x) # array([150, 200, 250, 300, 350, 400, 600], dtype=int64)
数据归一化


概念
1、数据集 dataset
2、每一行的数据叫做样本数据
3、除最后一列标签列外,每一列的数据叫特征或属性
4、最后一列叫做标签列,样本所属类别
5、属性(特征)空间:由特征张成的空间
6、特征向量:构成特征空间的每一行的特征数据
特征向量(features/feature vector):属性的集合,通常用一个向量表示,附属于一个实例。每一个样例都有自己不同的属性,不同的属性用不同的属性值代表,多个属性值组合在一起就可以用一个向量来表示。这个向量就称之为特征向量。

线性模型
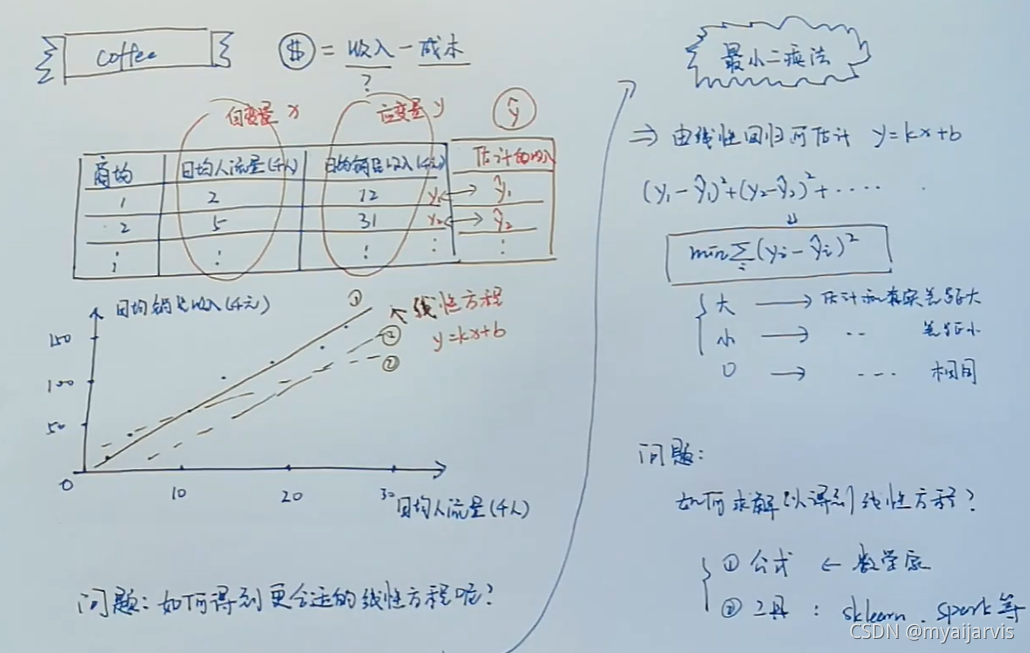
简单线性回归
咖啡店
https://www.bilibili.com/video/BV1sJ411z7zJ
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data=np.array([
['商场ID','日均人流量(千人)','日均销售收入(千元)'],
[1,2,12],[2,5,31],[3,8,45],[4,8,52],[5,13,79],
[6,15,85],[7,17,115],[8,19,119],[9,21,135],[10,24,145]
])
# 采用散点图的形式画出来
x=data[1:, 1] # 取第二列(去掉第一行)
y=data[1:, 2] # 取第三列(去掉第一行)
plt.scatter(x,y)
plt.show()
from sklearn.linear_model import LinearRegression
features= data[1:,1].reshape(-1,1)
target=data[1:,2]
regression=LinearRegression()
model= regression.fit(features, target)
model.intercept_ # 截距
model.coef_ # 回归系数k y=kx
model.predict([[10]]) # 预测,当日均人流量为10(千人)的日均销售收入(千元)
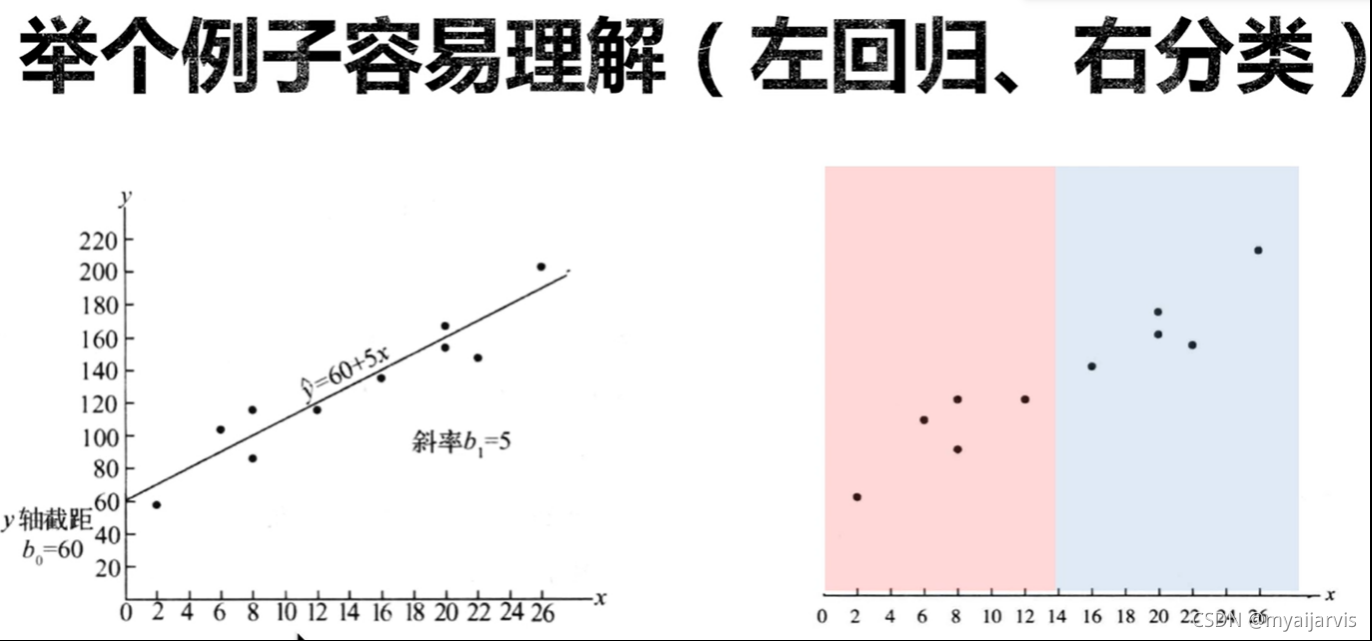
逻辑回归
回归模型的输出是连续的
分类模型的输出时离散的


决策树
官方入门 https://scikit-learn.org/stable/modules/tree.html#tree
理论+ 代码实例
神经网络
支持向量机SVM
2021.10.26
笔记:
SVM本质模型是特征空间中最大化间隔的线性分类器,是一种二分类模型。
之所以叫支持向量机,因为其核心理念是:支持向量样本会对识别的问题起关键性作用。那什么是支持向量(Support vector)呢?支持向量也就是离分类超平面(Hyper plane)最近的样本点。
简单地说,作为支持向量的样本点非常非常重要,以至于其他的样本点可以视而不见。
所谓间隔最大化,说的是分类超平面跟两类数据的间隔要尽可能大(即远离两边数据),对于分类超平面来说,也就是要位于两类数据的正中间,不偏向任何一类,才能保证离两边数据都尽可能远,从而实现间隔最大化。
存在有多个可行的线性分类器能将两类样本分类。SVM的最终目标是:以间隔最大化为原则找到最合适的那个分类器。
如何处理线性不可分?
SVM的解决办法就是先将数据变成线性可分的,再构造出最优分类超平面。
SVM 通过选择一个核函数K ,将低维非线性数据映射到高维空间中。原始空间中的非线性数据经过核函数映射转换后,在高维空间中变成线性可分的数据,从而可以构造出最优分类超平面。
核函数(Kernel Function)是计算两个向量在隐式映射后空间中的内积的函数。核函数通过先对特征向量做内积,然后用函数 K 进行变换,这有利于避开直接在高维空间中计算,大大简化问题求解。并且这等价于先对向量做核映射然后再做内积。
SVM求解算法知多少? 看文章
代码实例
将cross_validation换成model_selection
集成学习
参考:sklearn中调用集成学习算法 ***
# 使用集成学习的方法进行数据训练和预测
# 导入原始基础数据集并且进行数据的预处理
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
x, y = datasets.make_moons(n_samples=500, noise=0.3, random_state=42) # 生成制作月亮型数据
# y [1 0 1 0 0 1 ...]
# print(x.shape) # (500, 2)
# print(y.shape) # (500,)
plt.figure()
'''
参数c就是color,赋值为可迭代参数对象,长度与x,y相同,根据值的不同使得(x,y)参数对表现为不同的颜色。简单地说,按x,y值其中某一个值来区分颜色就好,
比如上边想按照y值来区分,所以直接c=y就可以了,
又比如画三维图像时,按照z值区分,直接将c=z就好了
'''
plt.scatter(x[:, 0], x[:, 1], c=y)
# 相当于下面两句
# plt.scatter(x[y == 0, 0], x[y == 0, 1], color="r")
# plt.scatter(x[y == 1, 0], x[y == 1, 1], color="g")
plt.show()
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42)
# 导入sklearn中的不同机器学习算法
# 逻辑回归算法
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(x_train, y_train)
print(log_reg.score(x_test, y_test)) # 0.864
# 支撑向量机SVM算法
from sklearn.svm import SVC
svc_reg = SVC()
svc_reg.fit(x_train, y_train)
print(svc_reg.score(x_test, y_test))
# KNN算法
from sklearn.neighbors import KNeighborsClassifier # k邻近回归
knn_reg = KNeighborsClassifier(n_neighbors=3) # 最近邻数据点个数
knn_reg.fit(x_train, y_train)
print(knn_reg.score(x_test, y_test)) # 0.896
# 决策树算法
from sklearn.tree import DecisionTreeClassifier # 分类树
tree_reg = DecisionTreeClassifier()
tree_reg.fit(x_train, y_train)
print(tree_reg.score(x_test, y_test)) # 0.896
# 自己简单采用集成学习的方法来进行相应的预测
from sklearn.metrics import accuracy_score # 准确度
y_predict1 = log_reg.predict(x_test)
y_predict2 = knn_reg.predict(x_test)
y_predict3 = tree_reg.predict(x_test)
y_predict = np.array(y_predict1 + y_predict2 + y_predict3 >= 3, dtype="int") # 相当于与运算 有0为0,全1为1
print(accuracy_score(y_predict, y_test)) # 0.864
# 使用sklearn中的集成学习接口进行相应的训练和预测—hard voting是投票时少数服从多数的原则
# (可以先把每个算法调到最好的结果,然后再用集成学习的算法进行预测)
from sklearn.ensemble import VotingClassifier
vote_reg = VotingClassifier(estimators=[
("log_cla", LogisticRegression()),
("svm_cla",SVC()),
("knn", KNeighborsClassifier()),
("tree", DecisionTreeClassifier(random_state=666))
], voting="hard")
vote_reg.fit(x_train, y_train)
print(vote_reg.score(x_test, y_test)) # 0.896
# 使用sklearn中的集成学习接口进行相应的训练和预测—soft voting是投票时不同算法不同权重的原则
# (可以先把每个算法调到最好的结果,然后再用集成学习的算法进行预测)
from sklearn.ensemble import VotingClassifier
vote_reg1 = VotingClassifier(estimators=[
("log_cla", LogisticRegression()),
("svm_cla",SVC(probability=True)), #SVC算法本来是计算不了概率的,但是经过一定的改进便可以计算概率,需要使得probability=true
("knn", KNeighborsClassifier()),
("tree", DecisionTreeClassifier(random_state=666))
], voting="soft")
vote_reg1.fit(x_train, y_train)
print(vote_reg1.score(x_test, y_test)) # 0.92
结果:
逻辑回归 0.864
SVM 0.896
KNN 0.896
决策树 0.864
自定义 0.824
hard voting 0.896
soft voting 0.92
