[人工智能]机器学习项目实践——慈善机构评分预测

回归任务之慈善机构评分预测

摘要：回归模型是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。回归模型重要的基础或者方法就是回归分析，回归分析是研究一个变量（被解释变量）关于另一个（些）变量（解释变量）的具体依赖关系的计算方法和理论，是建模和分析数据的重要工具。常用的回归模型有线性回归、岭回归、逐步回归、多项式回归等。使用回归分析有很多好处，比如它表明自变量和因变量之间的显著关系；它表明多个自变量对一个因变量的影响强度。而本实验将采用几种回归模型进行慈善机构的评分预测，通过训练出来的数据和均方误差来评估性能好坏。
关键词：回归 预测 线性回归 均方误差

一、问题介绍

在训练集中共有7400个样本，每个样本有23个特征，利用ascore,category，description，……，program_exp，fund_exp，admin_exp等23个特征，预测出score值。
特征具体介绍如下：
ascore：问责制和透明度得分（满分 100）。
category：机构类别，包含艺术，文化，人文，宗教和教育等等类别。
description：机构介绍，即机构简介。
ein：机构编号，每个机构编号唯一。
tot_exp：总费用（以美元计）（由计划 + 资金 + 行政这三部分组成）。
admin_exp_p：行政费用百分比（占总费用）。
fund_eff：以美元为单位的资金效率（筹集 1 美元捐款所花费的金额）。
fund_exp_p：资金费用百分比（总费用）。
program_exp_p：计划费用百分比（总费用）。
fscore：财务评分（满分 100）。
leader：机构领导者姓名。
leader_comp：机构领导者的薪酬（美元）。
leader_comp_p：领导百分比薪酬（即领导的薪酬占总薪酬的百分比）。
motto：标语，每个机构的宣传标语。
name：慈善机构名称。
tot_rev：该机构的总收入（美元）。
score：该机构所得的总分（满分 100）。
state：该机构的目前状态。
subcategory：子类，即该慈善机构还负责其他类型的活动。
size：慈善规模，有big,small,mid三种。
program_exp：以美元计的计划费用，即该机构在其提供的计划和服务上花费的金额。
fund_exp：以美元计的资金费用，即该机构筹集资金的金额。
admin_exp：行政费用（美元），即该机构管理费用、员工、会议费用。
测试集中共有1000个样本，每个样本有22个特征，没有训练集中的score这一项特征。

要求说明：
1.训练集与测试集中均有部分特征的值缺失，需要对缺失特征值做相应的处理。
2.有许多特征是文本特征，如需要利用这些特征，则需要进行预处理。
3.将用结果的均方根误差(RMSE)来评价模型的好坏。

二、算法概述

梯度树提升 Gradient Tree Boosting

Boosting是一类将弱学习器提升为强学习器的算法。这类算法的工作机制类似：先从初始训练集中训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注。
然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器的数目达到事先指定的值T，最终将这T个基学习器进行加权结合。
梯度提升（gradient boosting）属于Boost算法的一种，也可以说是Boost算法的一种改进，它与传统的Boost有着很大的区别，它的每一次计算都是为了减少上一次的残差(residual)，而为了减少这些残差，可以在残差减少的梯度(Gradient)方向上建立一个新模型。所以说，在Gradient Boost中，每个新模型的建立是为了使得先前模型残差往梯度方向减少，
与传统的Boost算法对正确、错误的样本进行加权有着极大的区别。
GBRT的优势有：
（1）自然而然地处理混合类型的数据
（2）预测能力强
（3）在输出空间对于异常值的鲁棒性强（通过强大的损失函数）
然而，GBRT也有劣势：
可扩展性方面，由于提升的时序性，不能进行并行处理

梯度树提升算法步骤：
对于给定的输入：训练数据集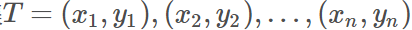
损失函数：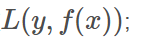
输出结果：一棵回归树f(x)

（1）首先初始化

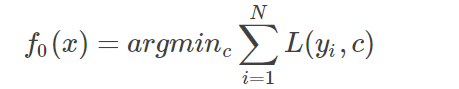
估计一个使损失函数极小化的常数值，此时它只有一个节点的树；

（2）迭代的建立M棵提升树
for m=1 to M:（第一层循环）
for i=1 to N：（第二层循环） 计算损失函数的负梯度在当前模型的值，并将它作为残差的估计值。

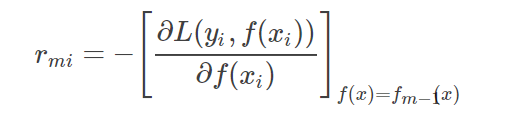
对于rmi拟合一棵回归树，得到第m棵树的叶节点区域Rmj,j=1,2,…,J
for j=1 to J：（第二层循环）,计算：

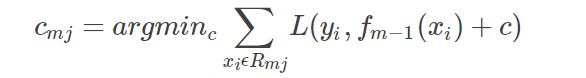
利用线性搜索估计叶节点区域的值，使损失函数极小化；然后，更新

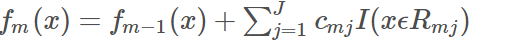
（3）最后得到的fm(x)就是我们最终的模型

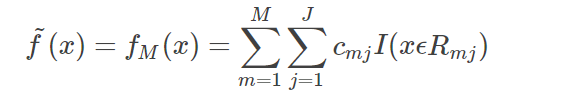
梯度提升决策树是监督学习中最强大也最常用的模型之一。其主要缺点是需要仔细调参，而且训练时间可能会比较长。与其他基于树的模型类似，这一算法不需要对数据进行缩放就可以表现的很好，而且也适用于二元特征与连续特征同时存在的数据集。与其他基于树的模型相同，它也通常不适用于高维稀疏矩阵。

三、具体步骤

3.1导入项目所需要的包：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics    # 计算均方误差

3.2读取训练集数据，共有7400个样本：

# 1.读取数据
train_data = pd.read_csv('train.csv')
train_data = train_data.iloc[:, :23]  # 截取，去除空列
train_data = train_data.drop(
    columns=['category', 'description', 'ein', 'leader', 'motto', 'name', 'state', 'subcategory', 'size'])  # 去除字符特征
# print(train_data)

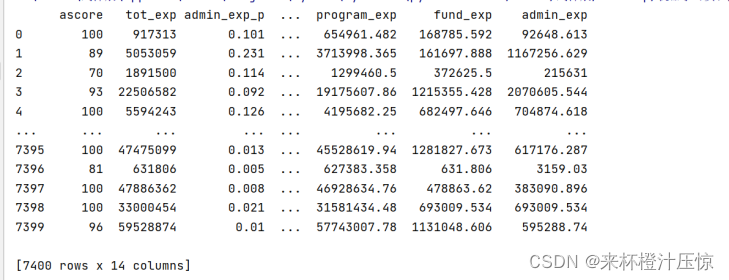
在CSV文件中可以看到有9列特征是字符特征，所以也要去掉，最后保留14个数字特征，效果如上图所示

3.3去除异常数据：

# 2.1去除异常数据
pd.set_option('display.width', None)  # 设置数据展示宽度
cols = train_data.columns
train_data = train_data[cols].apply(pd.to_numeric, errors='coerce')
train_data = train_data.dropna()
print(train_data)

for i in range(len(train_data)):
    x=np.delete(train_data,axis=0)  #删除样本异常数据值
    train_data=train_data.dropna()
print(train_data)

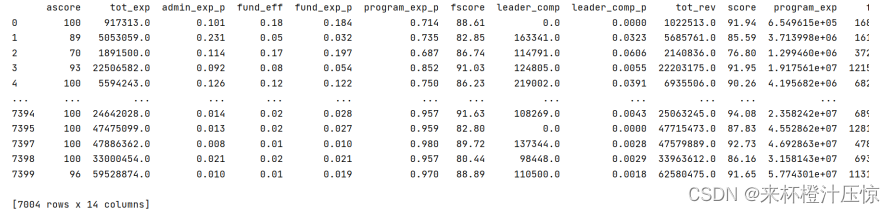
可以看到经过处理得到真正有用的数据有7004行

3.4提取csv文件中目标值score：

# 2.2将文件中score值单独提取出来
score = train_data.iloc[:, 10:11]
y_data = np.array(score)
train_data = train_data.drop(columns=['score'])  # 从原数据帧中删除score列
print(y_data)

3.5提取特征，绘制特征与score值相关的散点图，查看相关性：

# 2.3提取特征，绘制散点图
feature_np = train_data.columns
feature_np = np.array(feature_np)
# print(feature_name)
# 提取各特征数值

from sklearn.preprocessing import StandardScaler
scalar = StandardScaler()
train_data = np.array(train_data)
ax = scalar.fit_transform(train_data)  # 标准化处理，减小数据噪声，便于绘制散点图
# print(x_array)
# 绘制特征与score关系的散点图，查看特征是否相关

for i in range(13):
    plt.scatter(ax[:, i], y_data, s=5)
    plt.title(feature_np[i])
    plt.show()

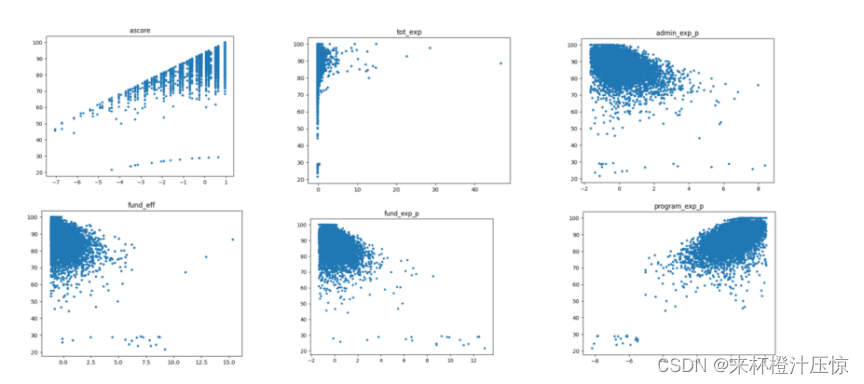
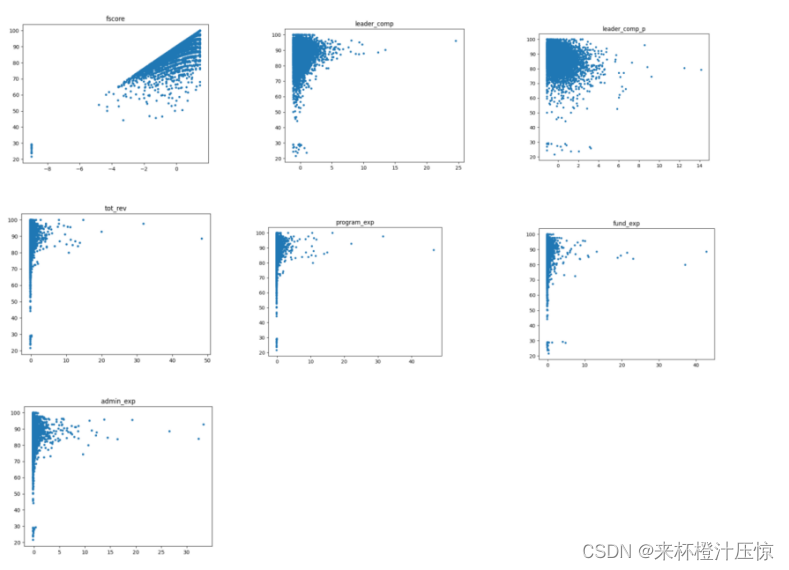
根据上面的散点图分析可知，ascore（问责制和透明度得分）, admin_exp_p（行政费用百分比） program_exp_p（计划费用百分比）, fscore（财务评分）这四个特征与score最相关，所以用这四个特征往后进行分析，同时删除其余不相关的特征。

3.6删除不相关特征：

# 2.4删除不相关的特征
item = []
for i in range(13):
    if feature_np[i] == 'ascore' or feature_np[i] == 'program_exp_p' or feature_np [i] == 'fscore' or feature_np[
        i] == 'admin_exp_p':
        continue;
    item.append(i)
train_data = np.delete(train_data, item, axis=1)
x_data = train_data
# print(x_data)

3.7模型训练，读取测试集数据：

# 3.1读取测试集数据
test_data = pd.read_csv('test.csv')
test_data = test_data.drop(
    columns=['category', 'description', 'ein', 'leader', 'motto', 'name', 'state', 'subcategory', 'size'])
# print(test_data)

3.8提取特征,剔除多余特征和不相关数据：

# 3.2提取特征,剔除多余特征和不相关数据
name = test_data.columns
name = np.array(name)
# print(name)
item_ = []
for i in range(13):
    if name[i] == 'ascore' or name[i] == 'program_exp_p' or name[i] == 'fscore' or name[i] == 'admin_exp_p':
        continue;
    item_.append(i)

test_x = np.array(test_data)
test_x = np.delete(test_x, item_, axis=1)
# print(test_x)

3.9利用模型预测score：

# 3.3预测score结果
from sklearn.ensemble import GradientBoostingRegressor

gbr = GradientBoostingRegressor(max_depth=4, n_estimators=3460, subsample=0.53, learning_rate=0.02)
gbr.fit(x_data, y_data.ravel())
predict_score = gbr.predict(test_x)
# print(predict_score)
# 3.4保存为csv文件

origin_data = pd.read_csv('test.csv')
result = pd.concat([origin_data, pd.DataFrame(predict_score)], axis=1)
result.to_csv('result.csv')

查看输出的csv文件：

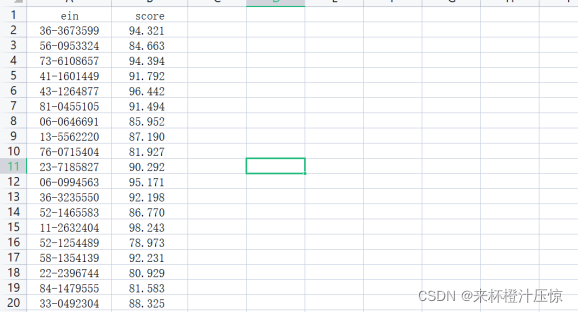
3.10计算均方误差：

#3.5计算均方误差
y_true = pd.read_csv('test-right.csv',usecols=['score'])
y_pred_gbr = pd.read_csv('result.csv',usecols=['score'])
print('RMSE by gbr:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_gbr)))

由此得出用梯度树回归算法得到的均方误差是0.11，效果较好

利用其它模型算预测score、算出RMSE

1.线性模型：

#3.6.1线性模型
from sklearn.linear_model import LinearRegression
lf = LinearRegression()
lf.fit(x_data, y_data.ravel())  # 训练数据,学习模型参数
predict_score_lf = lf.predict(test_x)  # 预测
#print('score by lf:',predict_score_lf)
y_true = pd.read_csv('test-right.csv',usecols=['score'])
y_pred_lf = predict_score_lf
print('RMSE by lf:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_lf)))

2.岭回归模型：
岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

#3.6.2岭回归
from sklearn.linear_model import RidgeCV
rr = RidgeCV(alphas=np.array([.1, .2, .3, .4]))
rr.fit(x_data, y_data.ravel())
predict_score_rr=rr.predict(test_x)
#print('score by rr:',predict_score_rr)
y_true = pd.read_csv('test-right.csv',usecols=['score'])
y_pred_rr = predict_score_rr
print('RMSE by rr:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_rr)))

3.Lasso回归模型：
LASSO是由1996年Robert Tibshirani首次提出，全称Least absolute shrinkage and selection operator。该方法是一种压缩估计。它通过构造一个惩罚函数得到一个较为精炼的模型，使得它压缩一些回归系数，即强制系数绝对值之和小于某个固定值；同时设定一些回归系数为零。因此保留了子集收缩的优点，是一种处理具有复共线性数据的有偏估计。

#3.6.3Lasson回归
from sklearn import linear_model
lassr = linear_model.Lasso(alpha=.0001)
lassr.fit(x_data,y_data.ravel())
predict_score_lassr = lassr.predict(test_x)
#print('score by lassr:',predict_score_lassr)
y_pred_lassr = predict_score_lassr
print('RMSE by lassr:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_lassr)))

4.随机森林回归
随机森林属于Bagging类算法，而Bagging 又属于集成学习一种方法，集成学习的大致思路是训练多个弱模型打包起来组成一个强模型，强模型的性能要比单个弱模型好很多，其中的弱模型可以是决策树、SVM等模型，在随机森林中，弱模型选用决策树。
在训练阶段，随机森林使用bootstrap采样从输入训练数据集中采集多个不同的子训练数据集来依次训练多个不同决策树；在预测阶段，随机森林将内部多个决策树的预测结果取平均得到最终的结果。
随机森林具体算法步骤如下：
（1）从训练集中随机抽取一定数量的样本，作为每棵树的根节点样本；
（2）在建立决策树时，随机抽取一定数量的候选属性，从中选择最合适属性作为分裂节点；
（3）建立好随机森林以后，对于测试样本，进入每一颗决策树进行类型输出或回归输出；若是分类问题，以投票的方式输出最终类别，若是回归问题，每一颗决策树输出的均值作为最终结果。

#3.6.4随机森林回归
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(random_state=0, n_estimators=1000, n_jobs=-1)
rf.fit(x_data,y_data.ravel())
predict_score_rf = rf.predict(test_x)
#print('score by rf:',predict_score_rf)
y_pred_rf = predict_score_rf
print('RMSE by rf:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_rf)))

四、结果分析

比较五种回归模型的均方误差：

有五种模型RMSE可知，在该慈善机构的评分预测中，采用梯度提升和随机森林算法得到了良好的结果

项目详细的数据集和测试集在链接处：
https://download.csdn.net/download/weixin_47686861/59645119

源码如下

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics    # 计算均方误差

# 1.读取数据
train_data = pd.read_csv('train.csv')
train_data = train_data.iloc[:, :23]  # 截取，去除空列
train_data = train_data.drop(
    columns=['category', 'description', 'ein', 'leader', 'motto', 'name', 'state', 'subcategory', 'size'])  # 去除字符特征
# print(train_data)
# 2.数据预处理
# 2.1去除异常数据
pd.set_option('display.width', None)  # 设置数据展示宽度
cols = train_data.columns
train_data = train_data[cols].apply(pd.to_numeric, errors='coerce')
train_data = train_data.dropna()
print(train_data)

for i in range(len(train_data)):
    x=np.delete(train_data,axis=0)  #删除样本异常数据值
    train_data=train_data.dropna()
print(train_data)

# 2.2将文件中score值单独提取出来
score = train_data.iloc[:, 10:11]
y_data = np.array(score)
train_data = train_data.drop(columns=['score'])  # 从原数据帧中删除score列
print(y_data)

# 2.3提取特征，绘制散点图
feature_np = train_data.columns
feature_np = np.array(feature_np)
# print(feature_name)
# 提取各特征数值

from sklearn.preprocessing import StandardScaler
scalar = StandardScaler()
train_data = np.array(train_data)
ax = scalar.fit_transform(train_data)  # 标准化处理，减小数据噪声，便于绘制散点图
# print(x_array)
# 绘制特征与score关系的散点图，查看特征是否相关

for i in range(13):
    plt.scatter(ax[:, i], y_data, s=5)
    plt.title(feature_np[i])
    plt.show()

# 2.4删除不相关的特征
item = []
for i in range(13):
    if feature_np[i] == 'ascore' or feature_np[i] == 'program_exp_p' or feature_np [i] == 'fscore' or feature_np[
        i] == 'admin_exp_p':
        continue;
    item.append(i)
train_data = np.delete(train_data, item, axis=1)
x_data = train_data
# print(x_data)


# 3.模型预测
# 3.1读取测试集数据
test_data = pd.read_csv('test.csv')
test_data = test_data.drop(
    columns=['category', 'description', 'ein', 'leader', 'motto', 'name', 'state', 'subcategory', 'size'])
# print(test_data)
# 3.2提取特征,剔除多余特征和不相关数据
name = test_data.columns
name = np.array(name)
# print(name)
item_ = []
for i in range(13):
    if name[i] == 'ascore' or name[i] == 'program_exp_p' or name[i] == 'fscore' or name[i] == 'admin_exp_p':
        continue;
    item_.append(i)

test_x = np.array(test_data)
test_x = np.delete(test_x, item_, axis=1)
# print(test_x)

# 3.3预测score结果
from sklearn.ensemble import GradientBoostingRegressor

gbr = GradientBoostingRegressor(max_depth=4, n_estimators=3460, subsample=0.53, learning_rate=0.02)
gbr.fit(x_data, y_data.ravel())
predict_score = gbr.predict(test_x)
# print(predict_score)
# 3.4保存为csv文件

origin_data = pd.read_csv('test.csv')
result = pd.concat([origin_data, pd.DataFrame(predict_score)], axis=1)
result.to_csv('result.csv')


#3.5计算均方误差
y_true = pd.read_csv('test-right.csv',usecols=['score'])
y_pred_gbr = pd.read_csv('result.csv',usecols=['score'])
print('RMSE by gbr:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_gbr)))


#3.6其他模型进行预测
#3.6.1线性模型
from sklearn.linear_model import LinearRegression
lf = LinearRegression()
lf.fit(x_data, y_data.ravel())  # 训练数据,学习模型参数
predict_score_lf = lf.predict(test_x)  # 预测
#print('score by lf:',predict_score_lf)
y_true = pd.read_csv('test-right.csv',usecols=['score'])
y_pred_lf = predict_score_lf
print('RMSE by lf:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_lf)))

#3.6.2岭回归
from sklearn.linear_model import RidgeCV
rr = RidgeCV(alphas=np.array([.1, .2, .3, .4]))
rr.fit(x_data, y_data.ravel())
predict_score_rr=rr.predict(test_x)
#print('score by rr:',predict_score_rr)
y_true = pd.read_csv('test-right.csv',usecols=['score'])
y_pred_rr = predict_score_rr
print('RMSE by rr:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_rr)))

#3.6.3Lasson回归
from sklearn import linear_model
lassr = linear_model.Lasso(alpha=.0001)
lassr.fit(x_data,y_data.ravel())
predict_score_lassr = lassr.predict(test_x)
#print('score by lassr:',predict_score_lassr)
y_pred_lassr = predict_score_lassr
print('RMSE by lassr:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_lassr)))



#3.6.4随机森林回归
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(random_state=0, n_estimators=1000, n_jobs=-1)
rf.fit(x_data,y_data.ravel())
predict_score_rf = rf.predict(test_x)
#print('score by rf:',predict_score_rf)
y_pred_rf = predict_score_rf
print('RMSE by rf:',np.sqrt(metrics.mean_squared_error(y_true, y_pred_rf)))