[人工智能]3 图像增强

3 图像增强

图像增强是将有用信息进行增强，将无用信息（干扰、噪声等）进行抑制，以提高图像的观察性。

3.1 灰度级变换

将图像的灰度值映射到新的灰度值。

3.1.1 线性灰度级变换

Image1 = imread('C:\Users\Administrator\Desktop\timg\lotus.jpg');
Image2 = rgb2gray(Image1);
Image3 = imadjust(Image2,stretchlim(Image2)); % stretchlim实现对比度拉伸
subplot(121),imshow(Image2);
subplot(122),imshow(Image3);

3.1.2 非线性灰度变换

常用的非线性灰度变换有：
对数变换（拉伸低灰度区）：c为尺度比例系数
$$g(x,y)=c?log[f(x,y)+1]$$

指数变换（拉伸高灰度区）：a用于决定指数变换函数曲线的初始位置,c
用于决定曲线的陡峭程度。
$$g(x,y)=b^{c[f(x,y)?a]}?1$$
幂变换：
$$g(x,y)=c?[f(x,y){]}^{\gamma }$$

Image4 = double(Image2);
% 对数变换
c1 = 255/log(256); % 尺度比例系数
result1 = uint8(c1*log(Image4+1));
% 指数变换
c2 = 255/(exp(2.56)-1);
result2 = uint8(c2*(exp(Image4*0.01)-1));
% 幂变换
gamma = 0.35;
result3 = Image4.^gamma;

3.1.3 基于直方图的灰度级变换

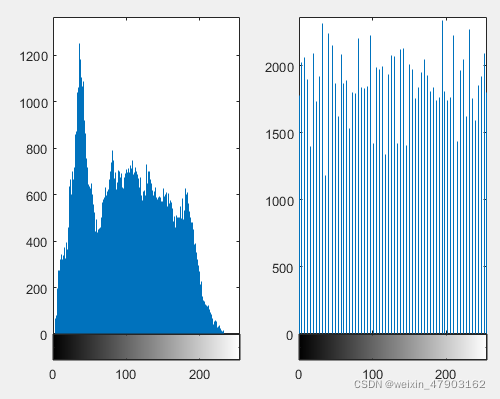
灰度直方图：横坐标为灰度级，纵坐标为灰度级出现的次数（频数、概率），反映了图像中灰度的分布状况。
1、直方图的均衡化
新的灰度值s，老的灰度值r，pr为原图的概率密度函数
$$s=T(r)={\int }_0^r{p}_r(w)dw$$
$$p_s(s)=p_r(r)?\frac{dr}{ds}=p_r(r)?\frac{1}{p_r(r)}=1$$
所以经过T变换为s后，可以产生为常数的均匀概率密度的图像，实现灰度值分布均匀，但是在实际处理中由于灰度级有限，并不能达到完全的均匀。
对于数字图像：
$$s_k=T(r_k)=\sum _{j=0}^k{p}_r(r_j)=\sum _0^k\frac{n_j}{N}$$
2、直方图的规定化
直方图的均衡化实现整个图像的增强。规范化则可以为一幅图指定一种特定的直方图，对图像进行有目的的增强，而不是全局。

% 直方图均衡化
result4 = histeq(Image2);
subplot(121),imhist(Image2);
subplot(122),imhist(result4);
%直方图规定化
%result4 = histeq(Image2,Hgram);  % Hgram为指定的直方图

3.2 空域滤波

空域滤波是指在像素点邻域内进行模板运算，将结果赋值给中心像素点。设滤波器为h(x,y)，对图像f(x,y)进行空域滤波可以表示为卷积运算形式。
$$g(x,y)=\sum _{m=?i}^i\sum _{n=?j}^{j}f(x?m,y?n)h(m,n)$$
平滑滤波器可以抑制噪声，锐化滤波器可以增强边缘细节。

3.2.1 噪声和平滑滤波

1、噪声
（1）加性噪声：$$g(x,y)=f(x,y)+n(x,y)$$
（2）乘性噪声：$$g(x,y)=f(x,y)+f(x,y)?n(x,y)$$
（3）高斯噪声：噪声分布在每一个像素点上，幅度值是随机的，分布近似符合正态分布；
（4）椒盐噪声：幅度值近似相等，但位置是随机的。

% 给图片加噪声
noiseImage1 = imnoise(Image2,'gaussian');
noiseImage2 = imnoise(Image2,'salt & pepper',0.01);

2、均值滤波
例如模板为：
$$H=\frac{1}{9}?\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}?\text{\hspace{1em}(3)}$$
3、高斯滤波
按高斯分布生成模板，中心取值大，周围取值小。

% 滤波器模板生成
muban = fspecial('gaussian',[5,5]);  % 类型，大小，参数
% 滤波
result5 = filter2(muban,noiseImage1);
subplot(121),imshow(noiseImage1);
subplot(122),imshow(result5,[]);

注意：subplot(122),imshow(result5,[]); 如果没有[]，会是一片白色，原因：
显示图像的范围的区别，显示uint8时从1-255，显示double时从0-1.
也可以除以255.
4、中值滤波
以像素邻域内灰度的中值（中位数）代替该像素点的值。

%中值滤波
result6 = medfilt2(noiseImage2,[5,5]);
subplot(121),imshow(noiseImage2);
subplot(122),imshow(result6,[]);

5、双边滤波
双边滤波同时考虑邻域内像素的空间邻近性和灰度相似性，进行局部加权平均，在消除噪声的同时保留边缘。设输入图像为f(x,y),滤波图像为g(x,y)，双边滤波如下：
$$g(x,y)=\frac{{\sum }_{i,j}f(i,j)w(x,y,i,j)}{{\sum }_{i,j}w(x,y,i,j)}$$
(x,y)为当前处理点，(i,j)为邻域内的点，w为加权系数
$$w(x,y,i,j)=e^{?[\frac{(i?x{)}^2+(j?y{)}^2}{2{\sigma }_d^2}]}?e^{?[\frac{|f(i,j)?f(x,y){|}^2}{2{\sigma }_r^2}]}$$
第一项表征空间，第二项表征灰度差。σd控制空间邻近度，σr控制灰度邻近度。

clear,clc,close all; % 清除操作
Image = imread('C:\Users\Administrator\Desktop\timg\lotus.jpg'); % 读取图片
Image = rgb2gray(Image);
Image = im2double(Image);
nIg = imnoise(Image,'gaussian');  % 加高斯噪声
result1 = filter2(fspecial('gaussian',[7,7],5),nIg);   % 高斯滤波
[height,width,color] = size(Image);
win = 3;
sigmad = 5;
sigmar = 0.2;    % 双边滤波参数
[X,Y] = meshgrid(-win:win,-win:win);  % 矩阵(i-x)   (j-y)
wd = exp(-(X.^2 + Y.^2)/(2*sigmad^2));  %空间权值
result2 = zeros(height,width,color);
for c = 1:color
	for j = 1:height
		for i = 1:width
			temp = nIg(max(j-win,1):min(j+win,height),max(i-win,1):min(i+win,width),c);  % //取出邻域矩阵f(i,j)
			wr = exp(-(temp-nIg(j,i,c)).^2/(2*sigmar^2)); % 灰度邻近权值
			W = wr.*wd((max(j-win,1):min(j+win,height))-j+win+1,(max(i-win,1):min(i+win,width))-i+win+1); % 取出对应形状的对应的空间矩阵，画个图理解一下
			result2(j,i,c) = sum(W(:).*temp(:))/sum(W(:));
		end
	end
end

subplot(221),imshow(Image),title('original image');
subplot(222),imshow(nIg),title('noise image');
subplot(223),imshow(result1),title('gaussian filtered image');
subplot(224),imshow(result2),title('bilateral filtered image');

3.2.2 边缘和锐化滤波

1、梯度
可以用微分的方法来检测图像的边缘。
图像中最常用的微分方法是计算梯度，梯度是方向导数取最大值的方向的向量，对于图像函数f(x,y)，在(x,y)的梯度为：
$$G[f(x,y)]=[\frac{?f}{?x}\frac{?f}{?y}]$$
可以用梯度幅值来代替梯度：
$$G[f(x,y)]=[(\frac{?f}{?x}{)}^2+(\frac{?f}{?y}){]}^{\frac{1}{2}}$$
为了计算方便，也可用绝对值；
对于图像这类离散的数字矩阵，用差分代替微分：
$$\frac{?f}{?x}=\frac{f(x+1,y)?f(x,y)}{x+1?x}=f(x+1,y)?f(x,y)$$
$$\frac{?f}{?y}=\frac{f(x,y+1)?f(x,y)}{y+1?y}=f(x,y+1)?f(x,y)$$
$$g(x,y)=|f(x+1,y)?f(x,y)|+|f(x,y+1)?f(x,y)|$$
梯度图像可以反映原图像灰度级的变化；而要实现边缘检测，可以设定一个阈值时，当变化大于这个阈值就将该点设置为边缘点。所以检测结果受阈值的调控。
图像锐化滤波的实质是将原图像和梯度图像相加，以增强图中的变化。

% 使用梯度算子进行图像锐化
[height,width,color]=size(Image);
edgeImage = zeros(height,width,color);
for c = 1:color
	for x = 1:width-1
		for y = 1:height-1
			edgeImage(y,x,c) = abs(Image(y,x+1,c)-Image(y,x,c))+abs(Image(y+1,x,c)-Image(y,x,c));
		end
	end
end

sharpImage = Image + edgeImage;
subplot(131),imshow(Image),title('original image');
subplot(132),imshow(edgeImage),title('gradient image');
subplot(133),imshow(sharpImage),title('sharp image');

2、Roberts算子、Sobel算子、Prewitt算子、Laplacian算子、LoG算子、Ganny算子等实现边缘检测

% 以roberts算子为例：
% 用roberts算子进行边缘检测
BW = edge(Image,'roberts');
% roberts模板
H1 = [1 0;0 -1];
H2 = [0 1;-1 0];
% 利用模板滤波
R1 = imfilter(Image,H1);
R2 = imfilter(Image,H2);
% 梯度图像
edgeImage = abs(R1) + abs(R2);
sharpImage = Image + edgeImage;

subplot(131),imshow(BW),title('edge');
subplot(132),imshow(edgeImage),title('gradient image');
subplot(133),imshow(sharpImage),title('sharp image');

3.3 频域滤波

$$f(x,y)?>F(u,v)$$$$G(u,v)=H(u,v)F(u,v)$$$$G(u,v)?>g(x,y)$$
H(u,v)为频域滤波器的传递函数

3.3.1 低通滤波

1、理想低通滤波器
$$H(u,v)=\{\begin{array}{ll}1,& D(u,v)<=D_0\\ 0,& D(u,v)>D_0\end{array}$$
$$D(u,v)=(u^2+v^2{)}^{\frac{1}{2}}$$
$$D_0$$为截止频率
2、巴特沃斯低通滤波器
最平低通滤波器，n阶截止频率为D0的滤波器的传递函数为：
$$H(u,v)=\frac{1}{1+[D(u,v)/D_0{]}^{2n}}$$
或
$$H(u,v)=\frac{1}{1+(\sqrt{2}?1)[D(u,v)/D_0{]}^{2n}}$$
3、指数低通滤波器
$$H(u,v)=e^{?[\frac{D(u,v)}{D_0}{]}^n}$$

% 巴特沃斯滤波器
nIg = imnoise(Image,'gaussian');
FImage = fftshift(fft2(double(nIg)));
[N,M] = size(FImage);
g = zeros(N,M);
r1 = floor(M/2);
r2 = floor(N/2);
len = sqrt(r1^2+r2^2);
d0 = 0.2*len;  % 截止频率
n = 3; % 阶数
for x = 1:M
	for y = 1:N
		d = sqrt((x-r1)^2+(y-r2)^2);
		h = 1/(1+(d/d0)^(2*n));
		g(y,x) = h * FImage(y,x);
	end
end

g = real(ifft2(ifftshift(g)));
figure,imshow(g),title(['巴特沃斯',d0]);

3.3.2 高通滤波器

图像的边缘对应于高频分量，所以增强图像锐化可以用高通滤波器实现。
常见的高通滤波器有：理想高通滤波器、巴特沃斯高通滤波器、指数滤波器、梯形滤波器。
将低通的表达式中D(u,v)/D0换为D(0)/D(u,v)

3.3.3 基于小波变换的图像增强

% 利用小波变换进行边缘检测
[ca,ch,cv,cd] = dwt2(Image,'db4');
result = idwt2(ca*0,ch,cv,cd,'db4'); % 低频分量置0，进行小波重构
result = result + 0.2; % 为了显示细节清楚
imshow(result)

3.4 基于照度-反射模型的图像增强

通常，自然景物图像f(x,y)可以表示为光源照度场i(x,y)和反射光的反射场r(x,y)的乘积，称为图像的照度-反射模型：
$$f(x,y)=i(x,y)?r(x,y)$$
其中，0<i(x,y)<∞；0<r(x,y)<1
由于照明亮度一般是缓慢变化的，所以认为照明函数的频谱集中在低频段；由于反射函数随图像细节不同在空间快速变化，所以认为反射函数的频谱集中在高频段。
实际处理中，通常会借助对数变换，将上式中的乘法变为加法来简化计算，且对数变换接近人眼亮度感知能力，能够增强图像的视觉效果。
1、同态滤波
$$z(x,y)=ln[f(x,y)]=ln[i(x,y)]+ln[r(x,y)]$$
经过傅里叶变换
$$Z[(u,v)]=I(u,v)+R(u,v)$$
定义同态滤波函数H
$$S(u,v)=H(u,v)Z(u,v)$$
傅里叶反变换
$$s(x,y)=i^{\prime }(x,y)+r^{\prime }(x,y)$$
指数变换
$$g(x,y)=exp[s(x,y)]=i_0(x,y)?r_0(x,y)$$
其中i0(x,y)为处理后的照射分量，r0(x,y)是处理后的反射分量。
2、基于Retinex理论的图像增强
视网膜大脑皮层理论
在中心环绕Retinex方法中，光照分量的估计是通过计算被处理像素与其周围区域的加权平均值实现的，
$$i_c^{\prime }(x,y)=h(x,y)?f_c(x,y)$$
c代表R、G、B；fc表示图像f的第c颜色的亮度分量；ic’是第c颜色通道的光照分量的估计值，h是中心环绕函数，一般可以用高斯函数。

资料：《MATLAB图像处理理论、算法与实例分析》（蔡利梅编著，清华大学出版社）