[人工智能] 与时间和频率测量有关的一些重要概念(抖动，游走，MTIE、TDEV)

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 与时间和频率测量有关的一些重要概念(抖动，游走，MTIE、TDEV) -> 正文阅读

[人工智能]与时间和频率测量有关的一些重要概念(抖动，游走，MTIE、TDEV)

1 与时频相关的技术指标说明

1.1 概述

在卫星导航中，我们常遇到秒脉冲的概念，其精度以峰峰值方式表示，一般峰峰值可以理解为秒脉冲误差分布的 3 $\sigma$ 。这里的3 $\sigma$ 是样本标准差，是方差算术平方根，克服了误差均值 $\mu$ 的影响。因此，可以看到，精度是抖动的表征，而准确度也就是偏差，则用误差的均值 $\mu$ 来表征。
在时频传递系统中，一方面我们关心重建时间的特征，主要是指重建的1PPS的上升沿，其与原始参考时间（可能是某一个原子钟生成的秒脉冲，也可能是一个UTC整秒）之间的对齐程度称作零值偏差。对于宽带卫星通信系统，与一般卫星导航系统一样，其核心网时间是一个“纸面时间”，由多个信关站的原子钟联合维护，该时间与UTC时间的差需要一个专门的校准系统进行持续维护，其与UTC时钟存在一个零值偏差。另一方面，我们关心驯服后的频率的特征。重建的秒脉冲本身也是一个特殊的1Hz时钟，除了1PPS外，一般通信系统都还另有至少一个频率时钟通常不低于10MHz的重建时钟。显然，重建的秒脉冲和时钟与原始秒脉冲和时钟之间是存在频率和相位误差的，如何评价这些误差呢？

1.2 频率指标

1.2.1 时钟频率

通常所说的原子钟频率数据，实际上指的是瞬时相对频率偏差数据，它的物理意义是相位变化对时间的微分，其表达式为
${y_{_i}} = \frac{{{x_{i + 1}} - {x_i}}}{{{\tau _0}}}$
式中 ${x_{i + 1}}$ 和 ${x_i}$ 分别表示第 $i + 1$ 和第 $i$ 历元的钟差（相位）值， ${\tau _0}$ 表示两个历元间的采样间隔。

####1.2.2 频率准确度

准确度是测量值或计算值与其定义的符合程度，其表达式为：
$\frac{{f - {f_0}}}{{{f_0}}}$
式中 $f$ 为被测信号的实际频率， $f_0$ 为测量信号的标称频率。实际实验中一般都要进行多次测量取平均求得对应的准确度指标，这是因为受测频标的实际输出频率并不是固定不变的。此外，现实情况下实际频率和标称频率之间的偏差无法直接测量，一般把参考信号的实际频率当做标准进行测量，且参考频率准确度应该比被测频标的准确度高出至少一个数量级。

1.2.3 频率漂移率

原子钟在连续运行的过程中，由于硬件设备的老化和周围环境变化等因素的影响，导致其输出的频率值经常会随运行时间呈现出线性递增或递减的现象。这种频率随时间单调变化的速率称为频率漂移率，也叫频率老化率，其表达式为：
${z_{_i}} = \frac{{{y_{i + 1}} - {y_i}}}{{{\tau _0}}}$
式中 ${y_{i + 1}}$ 和 ${y_{i}}$ 分别表示第 $i + 1$ 和第 $i$ 历元的频率值， ${\tau _0}$ 为相邻历元间的采样间隔。实际应用中，通常取多个历元瞬时频率漂移率的平均值，或利用最小二乘法获取最优频率漂移率。

1.2.4 频率稳定度

频率稳定度是表征时钟在一定时间内产生同样频率的能力，评估稳定度主要采用的指标是Allan方差，其表达式为：
$\sigma _y^2(\tau ) = \left\langle {\frac{{{{({y_{i + 1}} - {y_i})}^2}}}{2}} \right\rangle = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{{{({y_{i + 1}} - {y_i})}^2}}}{2}} = \frac{1}{{2n{\tau _0}^2}}\sum\limits_{i = 1}^n {{{({x_{i + 2}} - 2{x_{i + 1}} + {x_i})}^2}}$
式中 $n$ 为采样点的个数， $x_i$ 表示第 $i$ 历元的相位， $y_i$ 表示第i历元的频率值，为相邻历元间的采样间隔。随时间间隔 $n{\tau _0}$ 的取值从秒到数天的跨度，分别对应短期、中期和长期稳定度。下图直观的反映了频率准确度和稳定度之间的关系。

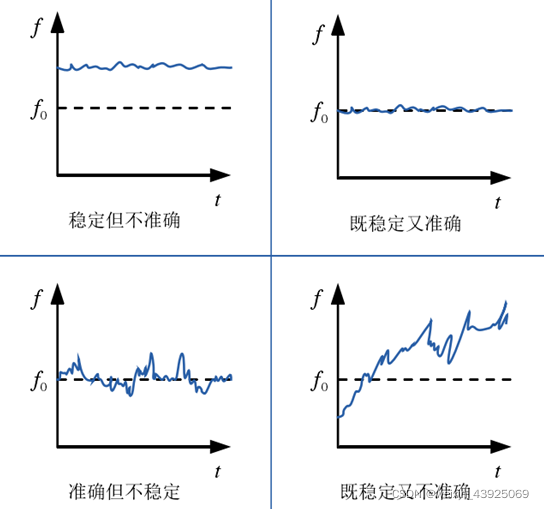
图1-1 频率稳定度和准确度示例

1.3 时钟抖动和游走指标

1.3.1 时钟抖动

生成的时钟相对于原始参考时钟，会存在抖动，如下图。

图1-2 时钟抖动

根据ITU-T G.810，低于10Hz的时钟抖动（Jitter）称作游走（Wander）。
时钟的抖动常用的简单方法通过峰峰值表征，比如GNSS接收机输出秒脉冲的抖动是±50ns，有时候也会用RMS来表示，这里的RMS是抖动对应的“高斯”分布的1σ。显然，这里认为的抖动对应的长期零偏为0的。
显然，这样的表征不能有效的表示出“游走”的特征。为此，《IEEE 2414-2020 Standard Jitter and Phase Noise》专门定义了TIE、MTIE、TDEV、ADEV等技术参数，来表征“游走”， MTIE和TDEV通常使用的较多。

1.3.2 TIE、PPTIE、MTIE

时间间隔误差（Time Interval Error，TIE）是指在特定时间点上，一个给定信号相对于参考时钟的相位差，测量的间隔为 ${\tau _0}$ ，下图中。TIE的测量周期为 ${\tau _0}=1s$ ，其起始时刻的初值通常设置为0，如下图的例子， $T = 100 s ， N = 100$ 。
TIE游走测量示意

图1-3 TIE游走测量示意
显然，给定一个窗口 $\tau {\rm{ = n}}{\tau _0}$ ，上图中为20s，都能够得到一个最大的TIE值，称作PPTIE，而最大时间间隔误差（Maximum Time Interval Error，MTIE）是指在一个测量周期 $T = 100 s$ 内，所有给定滑动窗口内的最大相位变化，也就是这段时间的PPTIE的最大值。其表达式和示意图如下：
$MTIE(n\tau ) = \mathop {\max }\limits_{1 \le k \le N - n + 1} (\mathop {\max }\limits_{k \le i \le k + n - 1} ({x_i}) - \mathop {\min }\limits_{k \le i \le k + n - 1} ({x_i}))$
式中 $N$ 表示全体观察点数目， $n$ 表示窗口内的观察点数目， $x_i$ 表示第 $i$ 历元的相位，。TIE和MTIE的测量示意图如下。

MTIE测量示例

图1-4 MTIE测量示例
在图1-3中，，MITE=11ns，大概发生在30ns的位置。图1-3中不同的对应的MTIE如下图所示。
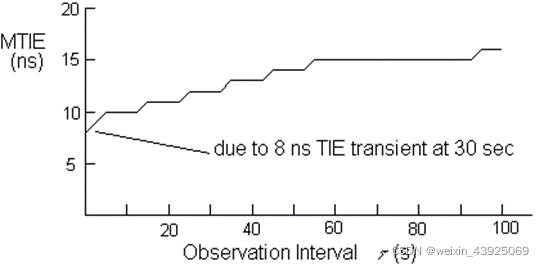
在这里插入图片描述

图1-5 图1-3的MTIE测量结果与 $\tau$ 的关系

1.3.3 TDEV和ADEV

TDEV（Time Deviation）指TIE的时间偏差测量结果，ADEV（Allan Deviation）指TIE的艾兰偏差测量结果，它们都是描述在一段时间窗口内的信号频率游走的指标，反映的是每次漂移偏离中心单位的数学期望，本质上，TDEV和ADEV反映的是游走的特定频谱分量的度量。
它们表达式分别如下：
$T\hat DEV(\tau ) = \sqrt {\frac{1}{{6(N - 3n + 1)}}\sum\limits_{j = 1}^{N - 3n + 1} {{{(\sum\limits_{i = j}^{j + n - 1} {({x_{i + 2n}} - 2{x_{i + n}} + {x_i})} )}^2}} }$
$A\hat DEV(\tau ) = \sqrt {\frac{1}{{2{\tau ^2}(N - 2n)}}\sum\limits_{j = 1}^{N - 2n} {{{({x_{i + 2n}} - 2{x_{i + n}} + {x_i})}^2}} }$
式中 $N$ 表示全体观察点数目， $n$ 表示窗口内的观察点数目， ${\tau _0}$ 表示采样时间间隔， $n{\tau _0}$ 表示观察窗口的大小， $x_i$ 表示第个TIE的值。
TDEV的表达式也可以写成迭代的形式：
$T\hat DEV(\tau ) = \sqrt {\frac{1}{6}\frac{1}{{N - 3n + 1}}\sum\limits_{j = 1}^{N - 3n + 1} {S_j^2(n)} }$
其中
$\begin{array}{l} {S_j}(n) = {S_{j - 1}}(n) - {x_{j - 1}} + 3{x_{j + n - 1}} - 3{x_{j + 2n - 1}} + {x_{j + 3n - 1}}\\ {S_1}(n) = \sum\limits_{i = 1}^n {({x_{i + 2n}} - 2{x_{i + n}} + {x_i})} \end{array}$
TDEV的测量和计算方法：
1、定义窗口大小；
2、从第一格开始，计算相邻两个窗口的边界变化 $S_j^{}(n)$ ；
3、每次将两个窗口向右滑动一格直到完成一个窗口，将得到的结果求和后平方；
4、继续重复2、3步直至完成整个观察时间内的计算；
5、求算术平均并开方得到TDEV。
下图是图1-3的TDEV测量结果与T、 $\tau$ 的关系。
TDEV测量结果与T、的关系