目录

1.转置卷积
简介:
我们一般可以通过卷积操作来实现高维特征到低维特征的转换。比如在一 维卷积中,一个5维的输入特征,经过一个大小为3的卷积核,其输出为3维特征。 如果设置步长大于1,可以进一步降低输出特征的维数。但在一些任务中,我们需 要将低维特征映射到高维特征,并且依然希望通过卷积操作来实现。
假设有一个高维向量为?和一个低维向量为?
如果用仿 射变换来实现高维到低维的映射,? 其中?
?为转换矩阵。我们可以很容易地通过转置 W来实现低维到高维 的反向映射, 即?
?
需要说明的是,上面两个公式并不是逆运算,两个映射只是形式上 的转置关系!
我们将低维特征映射到高维特征的卷积操作称为转置卷积(Transposed Convolution),也称为反卷积(Deconvolution)。
其实,在卷积网络中,卷积层的前向计算和反向传播也是一种转置关系。
对一个n维的向量z,和大小为m的卷积核,如果希望通过卷积操作来映射 (即宽卷积)。 到更高维的向量,只需要对向量z 进行两端补零p = m ? 1,然后进行卷积,可以 得到n + m ? 1维的向量。 转置卷积同样适用于二维卷积。下图给出了一个步长 s = 1,无零填充 p = 0的二维卷积和其对应的转置卷积。
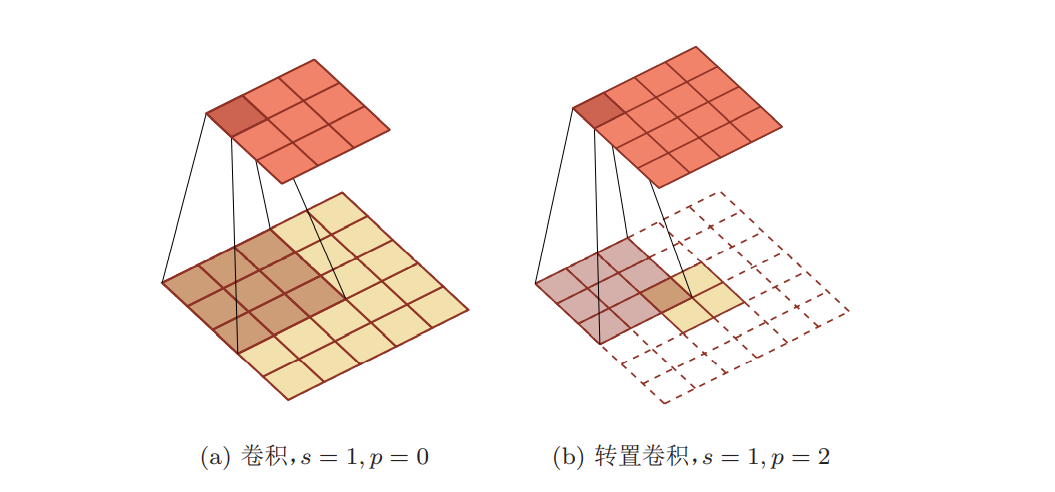
微步卷积 :
我们可以通过增加卷积操作的步长 s > 1 来实现对输入特征的下采样操作,大幅降低特征维数。同样,我们也可以通过减少转置卷积的步长 s < 1 来实现上采样操作,大幅提高特征维数。 步长s < 1的转置卷积也称为微步卷积 (Fractionally-Strided Convolution)。为了实现微步卷积,我们 可以在输入特征之间插入0来间接地使得步长变小!
补充内容:什么是降(下)采样?什么是上采样?
降(下)采样:
使得采样点数减小,可以通过每隔几个点在进行采样,比如常见的生成缩略图等。
升(上)采样:
一种通过插值的方式进行的采样,比如生成放大图等。
如果卷积操作的步长为s > 1,希望其对应的转置卷积的步长为 1/ s,需要在输入特征之间插入s ? 1个0来使得其移动的速度变慢。
以一维转置卷积为例,对一个n维的向量z,和大小为m的卷积核,通过对向 量z 进行两端补零p = m ? 1,并且在每两个向量元素之间插入d个0,然后进行 步长为1的卷积,可以得到(d + 1) × (n ? 1) + m维的向量。
下图给出了一个步长s = 2,无零填充p = 0的二维卷积和其对应的转置卷积:
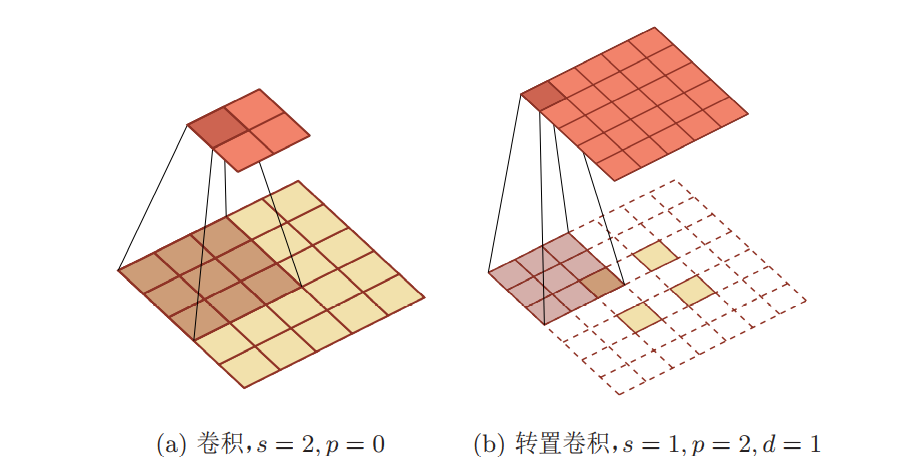
2.空洞卷积
简介:
对于一个卷积层,如果希望增加输出单元的感受野,一般可以通过三种方式 实现:
-
增加卷积核的大小;
-
增加层数,比如两层3 × 3的卷积可以近似一层 5×5卷积的效果;
-
在卷积之前进行汇聚操作。
缺点:
前两种方式会增加参数数量,而 第三种方式会丢失一些信息。
由此,空洞卷积应运而生!
空洞卷积(Atrous Convolution)是一种不增加参数数量,同时增加输出单元感受野的一种方法,也称为膨胀卷积(Dilated Convolution)
空洞卷积通过给卷积核插入“空洞”来变相地增加其大小。如果在卷积核的 每两个元素之间插入d ? 1个空洞,卷积核的有效大小为
其中d称为膨胀率(Dilation Rate)。当d = 1时卷积核为普通的卷积核。
空洞卷积实例:
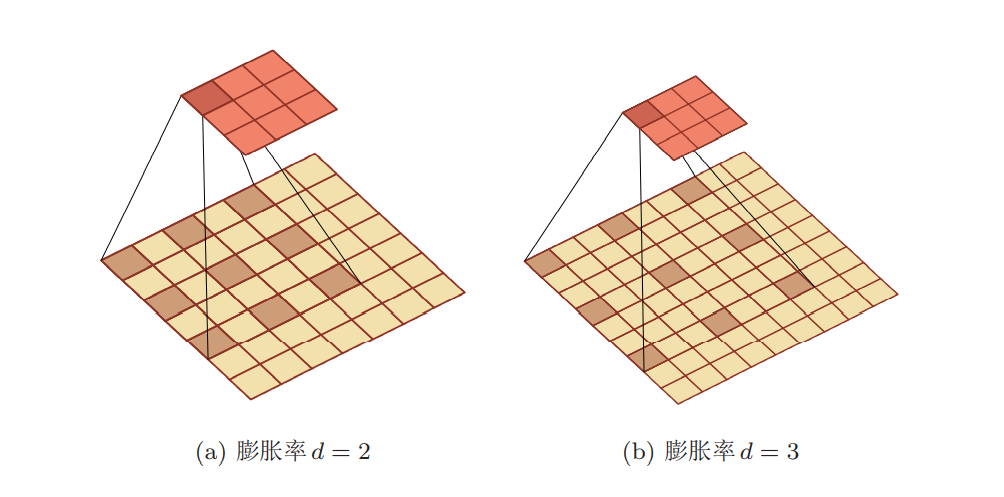
应用:
常见的DeNet网络和SSD网络就是应用的空洞卷积实例,详细见我的另两篇博客:
(2条消息) Backbone 之 DetNet:为检测而生(Pytorch实现及代码解析)_心之所向521的博客-CSDN博客
(2条消息) 单阶段多层检测器:SSD (理论及Pytorch代码详解)_心之所向521的博客-CSDN博客
3.总结
转置卷积:实现特征图低维到高维的目的!
空洞卷积:实现不增加参数量和丢失信息的情况下,有效的增加感受野的方法!