[人工智能]基于Pytorch的机器学习Regression问题实例（附源码）

写在前面

声明

本人既是Python新手也是机器学习新手，以下内容主要是为了作者自己的学习记录以及与他人的学习沟通。如果其中有错误，非常欢迎指正。如果误导了别人，那就非常抱歉了。。。。

本文目的

机器学习由于在声音、图像识别等等领域应用非常广泛，近年来是一个非常火热的发展方向。但是纵观各种学习书籍、视频等资料，要么先用大篇幅的文字讲了机器学习的理论但是没什么实践，要么直接用一些比较复杂的DNN或者CNN开始进行Demo，导致新手从入门到放弃。
本文希望从最简单的NN开始入手做一个Demo，不妨作为机器学习最开始的起点，然后再学习更复杂的机器学习理论。

学前准备

虽然上面说了本文可以作为机器学习最开始的起点，但是在此之前还是需要了解下机器学习的基本概念。个人非常推荐下面的文章：

【转】机器学习入门——浅谈神经网络

如果不会用笔算神经元网络就不算真正懂神经元网络

构建神经元网络

要解决什么问题

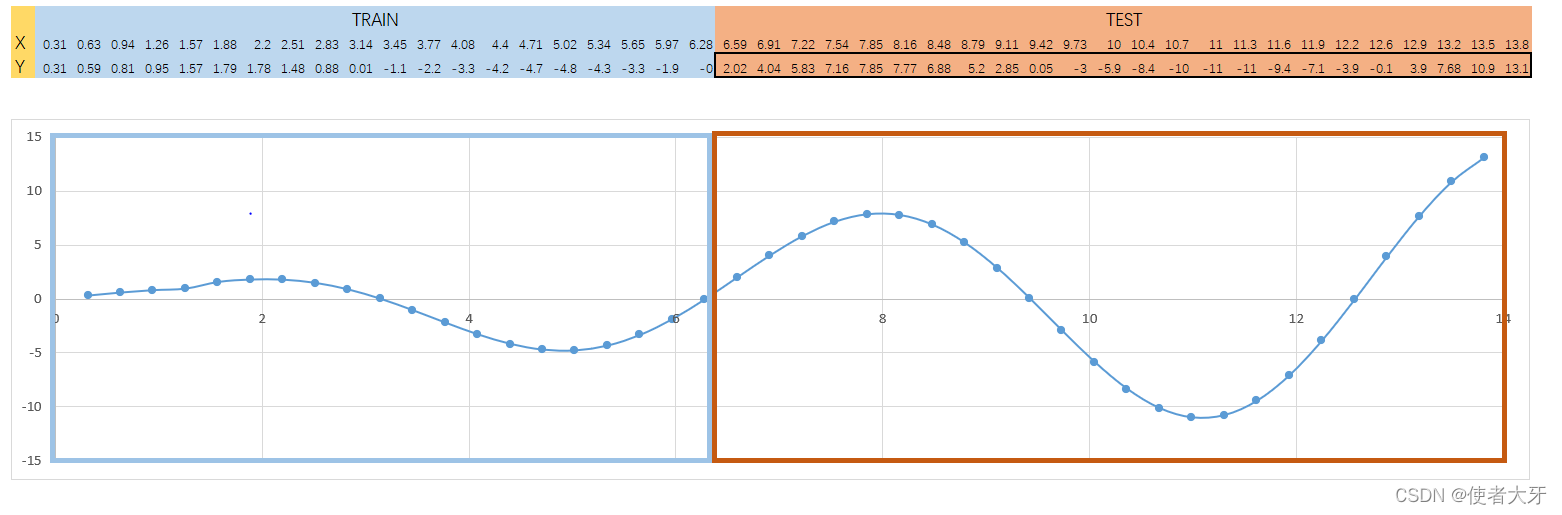
一个典型的Regression问题：我们已经有20个坐标点，要用一个神经元网络来拟合这20个坐标点，并且能预测后面的趋势走向。

打开上帝视角：我们预测的函数是y = x*sin(x)，前20个坐标点即为x在0~2π等分的20个点。当然，这在实际问题中我们不可能会知道我们要拟合和预测的是什么。

构建Python代码

神经元网络基本参数：
训练次数为100；
Learningrate为0.1；
优化方式为随机梯度下降（SGD）；
激活函数为Relu；
输入层神经元数=1；
隐藏层神经元数=6；
输出层神经元数=1；
loss函数为均方差（MSE）；

这真的是可以称为最简单的“神经元网络”了。。。

源代码如下，其实只要不到50行代码就可以了，细节请见代码备注。

import torch
import matplotlib.pyplot as plt
import math
import numpy

pi = math.pi

#导入训练组数据
x_train = numpy.arange(0,2*pi,pi/10)
y_train = x_train * numpy.sin(x_train)

#把x,y包装成tensor（神经元网络计算的输入只能是tensor或者variable）
x_train = torch.tensor(x_train, dtype=torch.float32)  #转换数据格式，要不然默认double会报错!!!
y_train = torch.tensor(y_train, dtype=torch.float32)
x_train = torch.unsqueeze(x_train,dim=1)   #array格式转换成tensor，并且要升一个维度（这样神经元网络才知道输入的是20个1维的学习数据，而不是1个20维的学习数据）!!!
y_train = torch.unsqueeze(y_train,dim=1)

#构建神经元网络
class NN(torch.nn.Module):
    def __init__(self,input_n,hidden1_n,output_n):  #input_n=输入层神经元数量（这个例子中是1），hidden1_n=第一个隐藏层神经元数量，output_n输出层神经元数量（这个例子中是1）
        super(NN, self).__init__()  #继承父class torch.nn.Module
        self.input = torch.nn.Linear(input_n,hidden1_n)    #构建输入层
        self.predict = torch.nn.Linear(hidden1_n,output_n)   #构建输出层

    def forward(self,x):
        x_mid = torch.relu(self.input(x))
        y = self.predict(x_mid)
        return y

nn = NN(1,6,1)
# print(nn)   #验证一下上面的代码是否会报错

optimizer = torch.optim.SGD(nn.parameters(),lr=0.1)  #优化方法为随机梯度下降
loss_f = torch.nn.MSELoss()

for i in range(100):  #训练100次
    y_predict = nn.forward(x_train)
    loss = loss_f(y_predict,y_train)
    optimizer.zero_grad() #这三句话用于优化learningrate，不写的话上面的SGD就没用了
    loss.backward()
    optimizer.step()

x_train = x_train.detach().numpy()  #把tensor型的张量数据再还原成numpy，要不然不能画图啊
y_train = y_train.detach().numpy()
y_predict = y_predict.detach().numpy()

plt.plot(x_train,y_train)  #画图看一下
plt.scatter(x_train,y_predict)
plt.show()

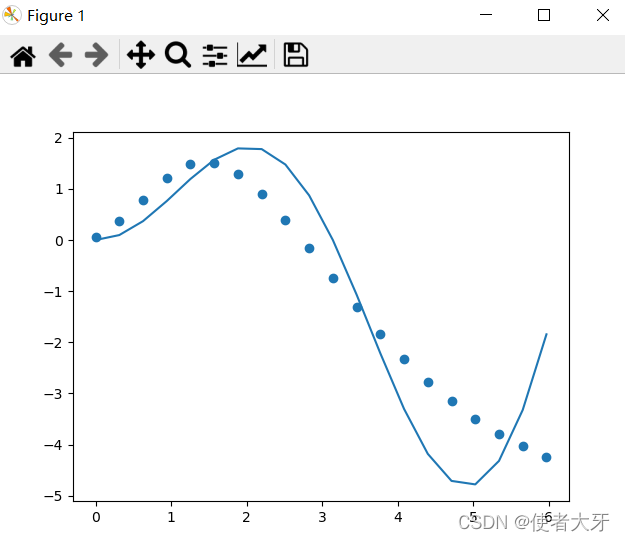
运行结果

这样，我们构建的神经元网络输出结果（x_train,y_predict）就是下图了

BUT！！！
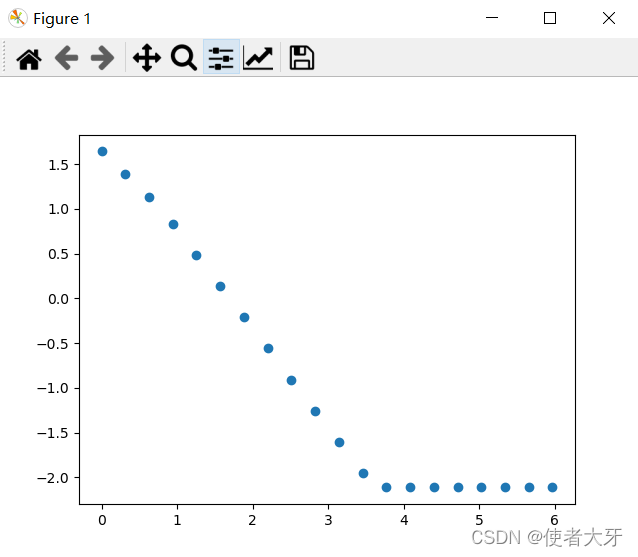
我们打开上帝视角看看，就会发现，上面的神经元网络得到的学习结果不仅不准，而且还不稳定（每次run的结果都不一样）。

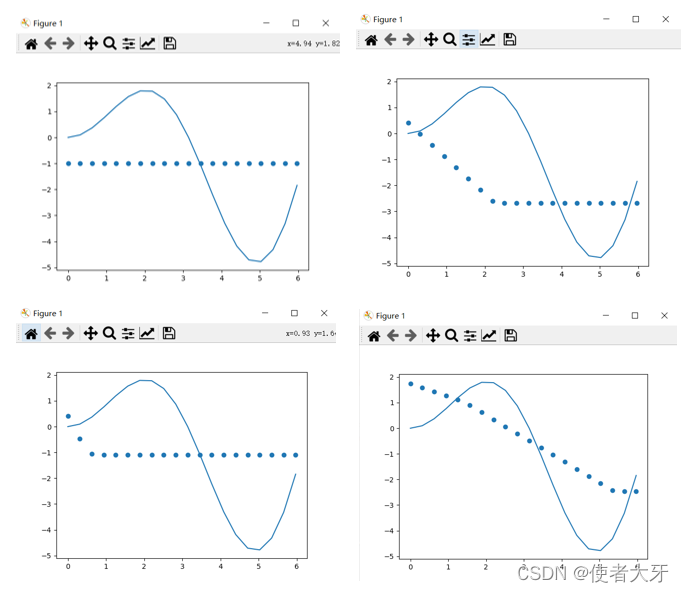
我忘了把每个图的loss放进来了，大家可以在源码上加print(loss)，看看loss和各个图形的关系

所以说，机器学习算是一种工程，需要实践出真知。下面再一起优化下这个神经元网络。

优化神经元网络

下面我们就用几种方法来使神经元网络能够有效地达“回归”的目的。

下面的每个方法，都是基于上一个方法进行的优化。

增加学习次数

上面每次学习的结果波动都很大，直观的感觉就是欠拟合。那么把学习次数由100次增加到10000次再看看。

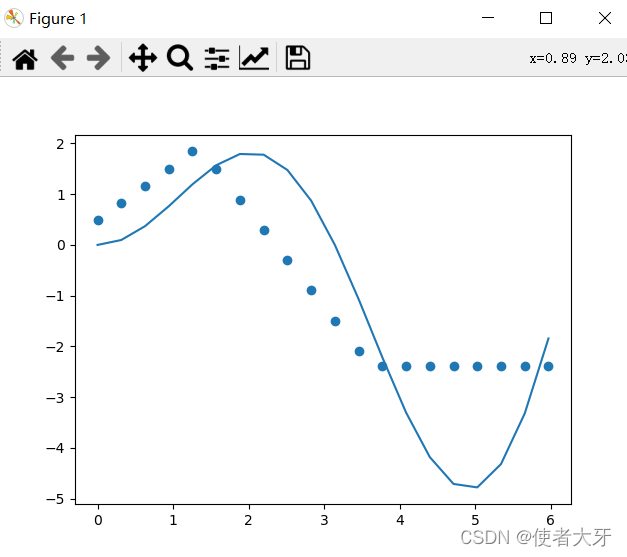
貌似结果好了一些，loss=1.7608。（学习次数100次的时候，loss=3~5）但是结果仍然很“粗糙”，波动也仍然较大。

把学习次数再增大100倍，到1000000，我的电脑就算不出来了。仅通过增大学习次数这种“蛮力”难以解决真正的技术问题，而且还会导致过拟合。

调整LearningRate

以下是LearningRate=0.01的结果

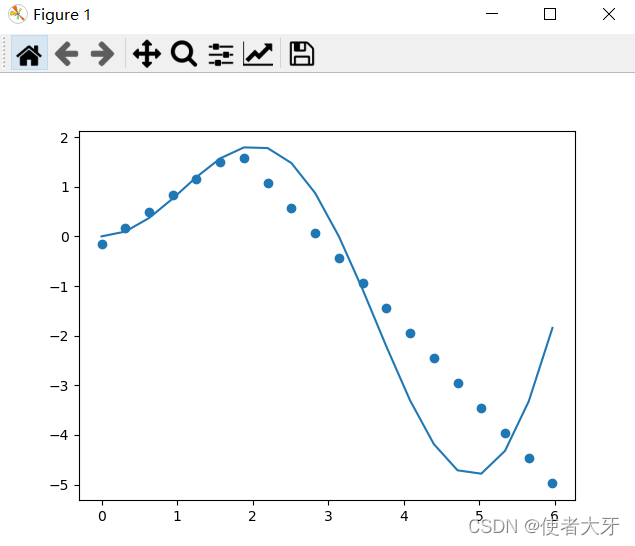
感觉不错，有内味了，loss=1.1876。

多运行几次我找到的最好结果如下

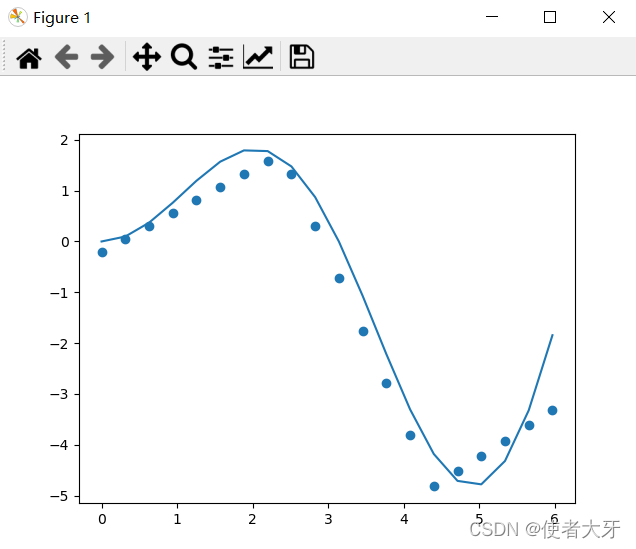
loss=0.2911。
这样就满意了？of course not！

调整优化方式

SGD（随机梯度下降）算是一种比较基础的优化算法（但是不妨碍它应用广泛），我们换成Adam试试。

关于不同的优化算法，再推荐一篇文章：深度学习各种优化函数详解

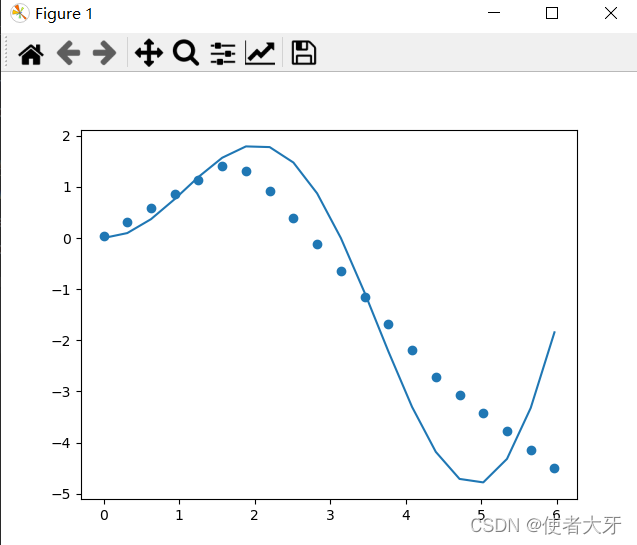
优化函数换成Adam后波动会小一些，上图的loss=0.9935，但是学习次数调回到了200。运行了很多次总结一下loss=0.2~2左右
上面用SGD方法的loss=0.2~3左右，但是学习次数是10000的前提。

但我觉得就在这个例子中，并不能说明哪个优化算法是更好的，为了节省时间，后面的算法基于Adam优化方法，学习200次再进行更新。

激活函数

Relu相对而言是个比较简单的激活函数，现在应用比较广泛的应该是Sigmoid函数，那我们就换成Sigmoid再试试。
这里就不上图了，运行结果loss=1.5~2.5左右。看起来波动（variation）和偏差（bias）都没有什么改善（甚至更差了）。

小结

其实我也是第一次比较系统的实操Pytorch，到目前为止好像只有在调整LearningRate之后，模型的loss有了比较明显的改善，后面的方法好像都作用不大。

有点后悔选用y=x*sin(x)这个目标，它似乎有点简单了，如果用更加复杂的目标函数，或许能看出来其他参数调整的作用

事已至此，有没有发现什么不对？
那就是无论怎么调整参数，虽然loss有改善，但是这个神经元网络输出的结果，就像是几条直线拼接出来的“生硬的”模型。仔细想想，这倒也合理，毕竟这个网络的神经元数，去掉输出输出层，只有一层隐藏层的6个神经元。

接下来搞点不一样的!

增加神经元个数

我们把原来隐藏层的6个神经元，增加到18个试试！
BUT！
增加神经元，要怎么加？它应该更瘦高还是更矮胖？那我们就都试一下。

Fat Learning（这个名字是我编的，如有雷同，纯属巧合）

网络结构变成：输入层=1，隐藏层=18，输出层=1

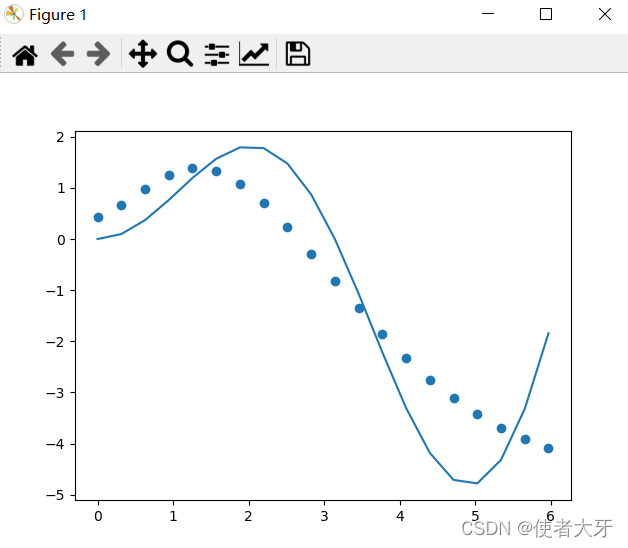
它看起来好像没那么“生硬”了，上图loss=0.99，整体loss=1.0~1.85左右。

我们玩个狠的，把隐藏层由18增加到100，loss=0.91，结果如下图。
说实话，我对你有些失望

Deep Learning

网络结构变成：输入层=1，隐藏层1=6，隐藏层2=6，隐藏层3=6，输出层=1
这里要对代码做一下比较大的调整

class NN(torch.nn.Module):
    def __init__(self,input_n,hidden1_n,hiddem2_n,hidden3_n, output_n):
        super(NN, self).__init__()  #继承父class torch.nn.Module
        self.input = torch.nn.Linear(input_n,hidden1_n)    #构建输入层
        self.hidden1 = torch.nn.Linear(hidden1_n,hiddem2_n)  #构建中间隐藏层
        self.hidden2 = torch.nn.Linear(hiddem2_n,hidden3_n)  #构建中间隐藏层
        self.predict = torch.nn.Linear(hidden3_n,output_n)   #构建输出层

    def forward(self,x):
        x_mid1 = torch.sigmoid(self.input(x))
        x_mid2 = torch.sigmoid(self.hidden1(x_mid1))
        x_mid3 = torch.sigmoid(self.hidden2(x_mid2))
        y = self.predict(x_mid3)
        return y

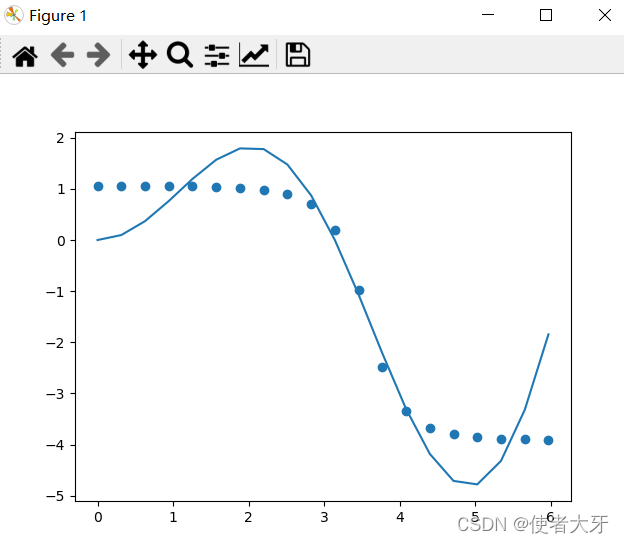
运行结果如上图，loss=0.56，整体loss=0.55~0.65，算是有个质变了。

这里也算间接地回答了一个问题，Why Deep Learning？

进行预测

对给定的数据进行拟合（回归）是这个神经元网络的基本任务，但是我们说到底还是想看看训练好的神经元网络进行“预测”的能力怎么样。

如开始所述，我们的train组数据是x在0~2π等分的20个点。
接下来，我们用x在0~4π等分4*7=28个点来验证下预测的结果准不准

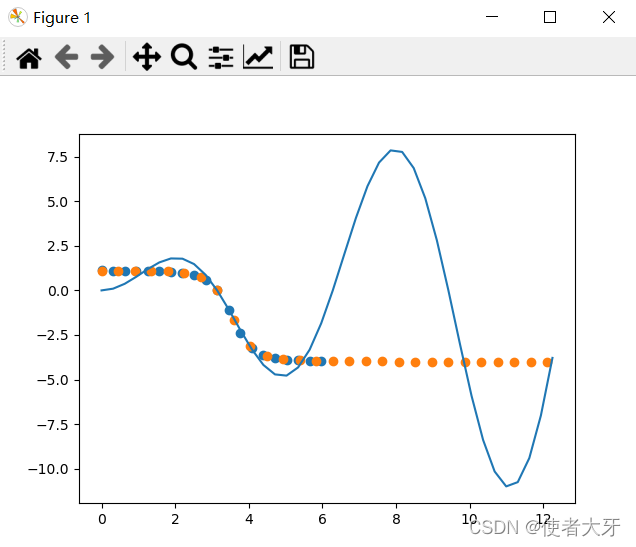
实际结果有点欲哭无泪，这个神经元网络在2π~4π的情况下预测的结果并不准。。。

这个预测问题，很遗憾，我没有搞定。。。。（讽刺的是我前面居然还认为y=x*sin(x)太简单了。。）
我尝试改了一个1×9×9×9×9×9×9×1的网络，但是结果和上面差不多。。。
如果有更好的方法，拜托教教我，先付优化后的代码为敬

import torch
import matplotlib.pyplot as plt
import math
import numpy

pi = math.pi

#导入训练组数据
x_train = numpy.arange(0,2*pi,pi/10)
y_train = x_train * numpy.sin(x_train)


#把x,y包装成tensor（神经元网络计算的输入只能是tensor或者variable）
x_train = torch.tensor(x_train, dtype=torch.float32)  #转换数据格式，要不然默认double会报错!!!
y_train = torch.tensor(y_train, dtype=torch.float32)
x_train = torch.unsqueeze(x_train,dim=1)   #array格式转换成tensor，并且要升一个维度（这样神经元网络才知道输入的是20个1维的学习数据，而不是1个20维的学习数据）!!!
y_train = torch.unsqueeze(y_train,dim=1)


#构建神经元网络
class NN(torch.nn.Module):
    def __init__(self,input_n,hidden1_n,hidden2_n,hidden3_n,hidden4_n,hidden5_n,hidden6_n, output_n):
        super(NN, self).__init__()  #继承父class torch.nn.Module
        self.input = torch.nn.Linear(input_n,hidden1_n)    #构建输入层
        self.hidden1 = torch.nn.Linear(hidden1_n,hidden2_n)  #构建中间隐藏层
        self.hidden2 = torch.nn.Linear(hidden2_n,hidden3_n)  #构建中间隐藏层
        self.hidden3 = torch.nn.Linear(hidden3_n, hidden4_n)
        self.hidden4 = torch.nn.Linear(hidden4_n, hidden5_n)
        self.hidden5 = torch.nn.Linear(hidden5_n, hidden6_n)
        self.predict = torch.nn.Linear(hidden6_n,output_n)   #构建输出层

    def forward(self,x):
        x_mid1 = torch.sigmoid(self.input(x))
        x_mid2 = torch.sigmoid(self.hidden1(x_mid1))
        x_mid3 = torch.sigmoid(self.hidden2(x_mid2))
        x_mid4 = torch.sigmoid(self.hidden3(x_mid3))
        x_mid5 = torch.sigmoid(self.hidden4(x_mid4))
        x_mid6 = torch.sigmoid(self.hidden5(x_mid5))
        y = self.predict(x_mid6)
        return y

nn = NN(1,9,9,9,9,9,9,1)
print(nn)   #确认一下网络结构

optimizer = torch.optim.Adam(nn.parameters(),lr=0.01)  #优化方法为Adam下降
loss_f = torch.nn.MSELoss()

for i in range(500):  #训练100次
    y_predict = nn.forward(x_train)
    loss = loss_f(y_predict,y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()


x_train = x_train.detach().numpy()  #把tensor型的张量数据再还原成numpy，要不然不能画图啊
y_train = y_train.detach().numpy()
y_predict = y_predict.detach().numpy()

print(loss)

#--------------------------------以下是用训练好的神经元网络进行预测-----------------------------------------------
x_test = numpy.arange(0*pi,4*pi,pi/7)
x_test = torch.tensor(x_test, dtype=torch.float32)
x_test = torch.unsqueeze(x_test,dim=1)

y_test = nn.forward(x_test)
x_test = x_test.detach().numpy()
y_test = y_test.detach().numpy()

x_plot = numpy.arange(0,4*pi,pi/10)
y_plot = x_plot * numpy.sin(x_plot)

plt.plot(x_plot,y_plot)
plt.scatter(x_train,y_predict)
plt.scatter(x_test,y_test)

plt.show()