目录
一、单变量线性回归 - Linear regession with one variable:
一、单变量线性回归 - Linear regession with one variable:
Supervised Learning: Gives the "right answer" for each example in the data.
- Regression Problem: Redict real-valued output
- Classfication Problem: Discrate-value output
1.常用字符标识：
- (x, y) = One training example
2.模型构建过程：
Univariate liner regression?
3.代价函数 - Cost Function：
Cost Function 代价函数（squared error function）数学表达式：
4.Cost Function Intuition:
- m：训练样本的个数；
- hθ(x)：用参数θ和x预测出来的y值；
- y：原训练样本中的y值，也就是标准答案
- 上角标(i)：第i个样本
????????代价函数衡量的是模型预测值h(θ) 与标准答案y之间的差异，所以总的代价函数J是h(θ)和y的函数，即J=f(h(θ), y)。又因为y都是训练样本中给定的，h(θ)由θ决定，所以，最终还是模型参数θ的改变导致了J的改变。对于不同的θ，对应不同的预测值h(θ)，也就对应着不同的代价函数J的取值。变化过程为：
????????θ引起了h(θ)的改变，进而改变了J(θ)的取值。为了更直观的看到参数对代价函数的影响，举个简单的例子：
????????有训练样本{(0, 0), (1, 1), (2, 2), (4, 4)}，即4对训练样本，每个样本对中第1个数表示x的值，第2个数表示y的值。这几个点很明显都是y=x这条直线上的点。如下图：
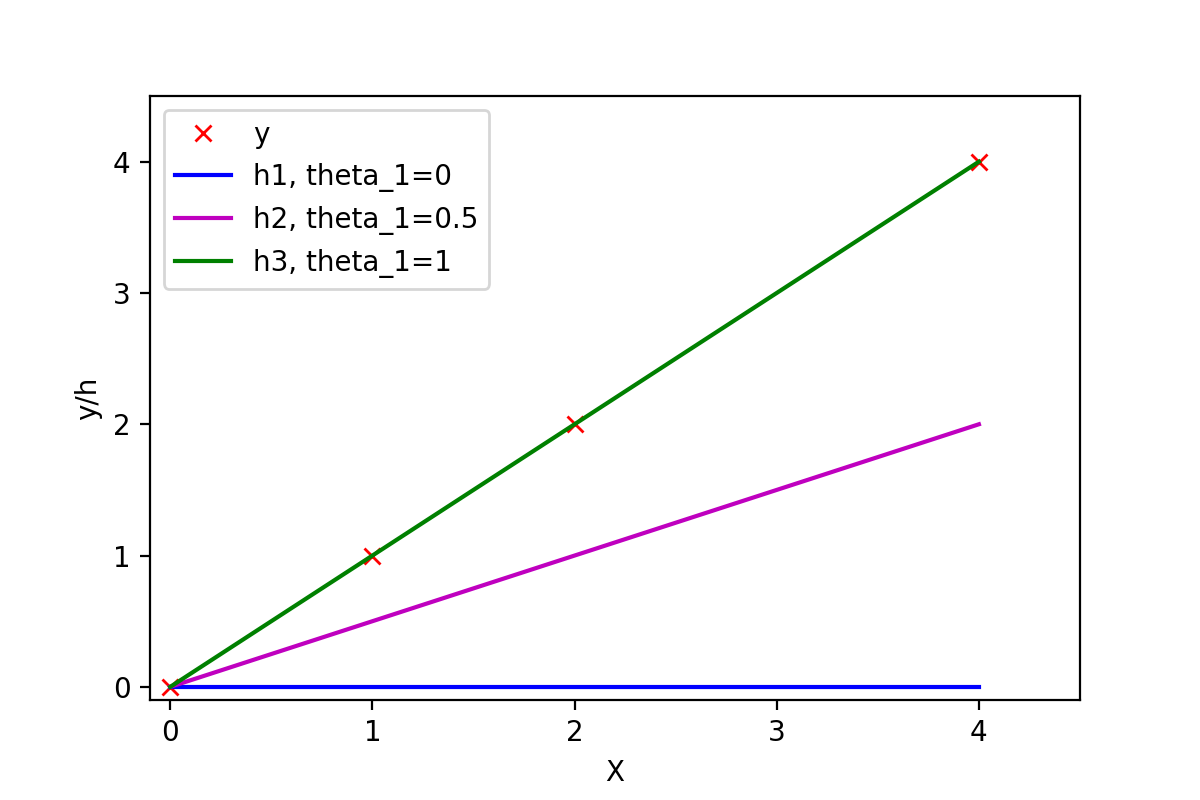
????????常数项为0，所以可以取θ0=0，然后取不同的θ1，可以得到不同的拟合直线。当θ1=0时，拟合的直线是y=0，即蓝色线段，此时距离样本点最远，代价函数的值（误差）也最大；当θ1=1时，拟合的直线是y=x，即绿色线段，此时拟合的直线经过每一个样本点，代价函数的值为0。
????????通过下图可以查看随着θ1的变化，J(θ)的变化情况：
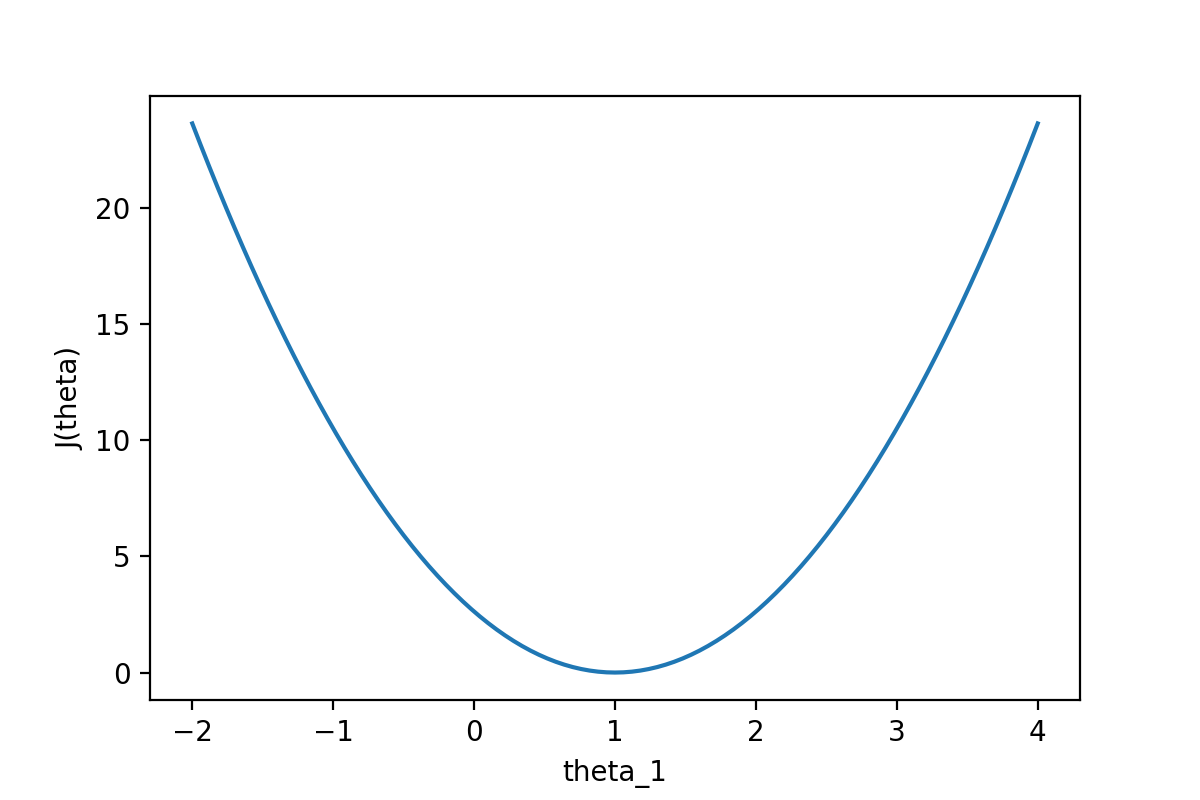
????????从图中可以很直观的看到θ对代价函数的影响，当θ1=1时，代价函数J(θ)取到最小值。因为线性回归模型的代价函数（均方误差）的性质非常好，因此也可以直接使用代数的方法，求J(θ)的一阶导数为0的点，就可以直接求出最优的θ值（正规方程法）。
二、Gradient Descent -??梯度下降:?
1.梯度下降概述：
目的：最小化函数J
通过不断变化参数??和?
?的值，获取函数J的最小值或者局部最小值。
2.梯度下降数学定义：
- := 表示赋值Assiagnment
- = 表示真假判断
?学习率learning rate，用来确定梯度下降时步长大小
- 同步更新
3.解析梯度下降：?
案例说明：?
?
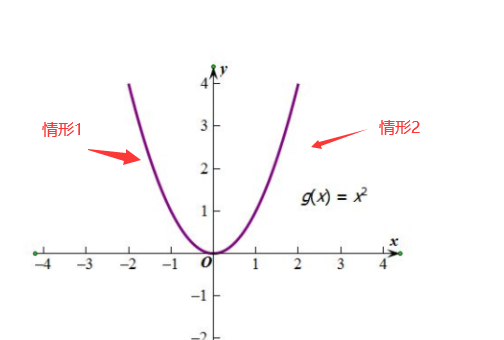
- 情形1：单调下降，导数为负（梯度为负），要想找到函数的最小值所对应的自变量的值（曲线最低点对应x的值）。x值会水平向右移动，也就是让x增大，此时随着x增大，导数（梯度）的绝对值是减小的
-
情形2：单调上升，导数为正（梯度为正），要想找到函数的自变量的值（曲线最低点对应x的值）。x向左移动，也就是让x减小，此时随着x减小，导数（梯度）的绝对值是减小的（也就是梯度下降）。
?注意：
- If?
- If?
????????当目前如果已经处于局部最优时，梯度下降法更新其实什么都没有做，因为在该点处的斜率值为0，他会始终保持在最优值处。
