前言

提示：以下是本篇文章正文内容

一、代价函数

假设神经网络的训练样本有𝑚个，每个包含一组输入𝑥和一组输出信号𝑦， 𝐿表示神经网络层数， 𝑆𝐼表示每层的 neuron 个数(𝑆𝑙表示输出层神经元个数)， 𝑆𝐿代表最后一层中处理单元的个数
在这里插入图片描述
将神经网络的分类分为两种情况：二类分类和多类分类

二类分类： 𝑆𝐿 = 0, 𝑦 = 0?𝑜𝑟?1表示哪一类；
𝐾类分类： 𝑆𝐿 = 𝑘, 𝑦𝑖 = 1表示分到第 i 类； (𝑘 > 2)

在正则化逻辑回归中，只有一个输出变量，也只有一个因变量𝑦
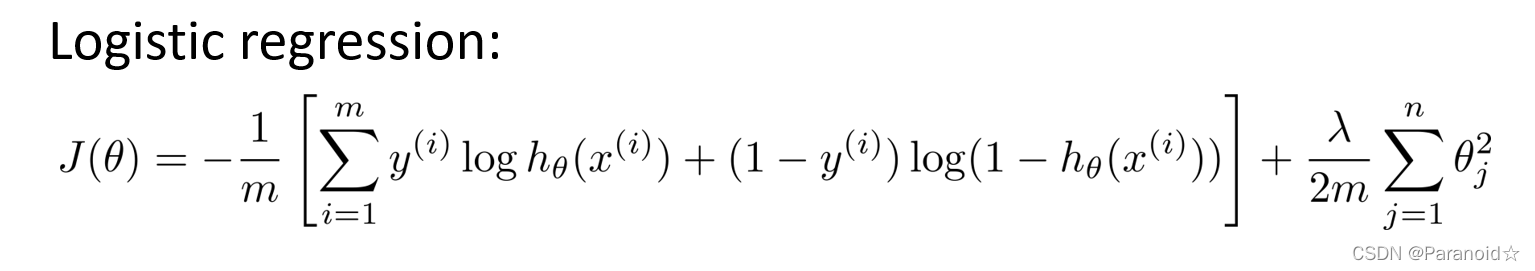
在这里插入图片描述
但是，在神经网络中，输出变量一般很多，假设函数?𝜃(𝑥)是一个维度为𝐾的向量，并且训练集中的因变量也是同维度的一个向量，神经网络中代价函数

注：正则化这项排除了每一层𝜃0后，每一层的𝜃 矩阵的和。最里层的循环𝑗循环所有的行（由𝑠𝑙 +1 层的激活单元数决定），循环𝑖则循环所有的列，由该层（ 𝑠𝑙层）的激活单元数所决定

和前面的逻辑回归一样，通过代价函数来观察算法预测的结果与真实值的误差，只是对于每一行特征，都会给出𝐾个预测，基本上可以利用循环，对每一行特征都预测𝐾个不同结果，然后在利用循环在𝐾个预测中选择可能性最高的一个，将其与𝑦中的实际数据进行比较

二、反向传播算法

在计算神经网络预测结果的时候采用了一种正向传播方法，从第一层开始正向一层一层进行计算，直到最后一层的?𝜃(𝑥)

反向传播算法：首先计算最后一层的误差，然后再一层一层反向求出各层的误差，直到倒数第二层（第一层是输入变量，不存在误差)
目的：为了计算代价函数的偏导数，以求得最小的代价函数
在这里插入图片描述

假设训练集只有一个实例(𝑥⁽¹⁾, 𝑦⁽¹⁾)，神经网络是一个四层的神经网络，其中𝐾 = 4， 𝑆𝐿 = 4， 𝐿 = 4
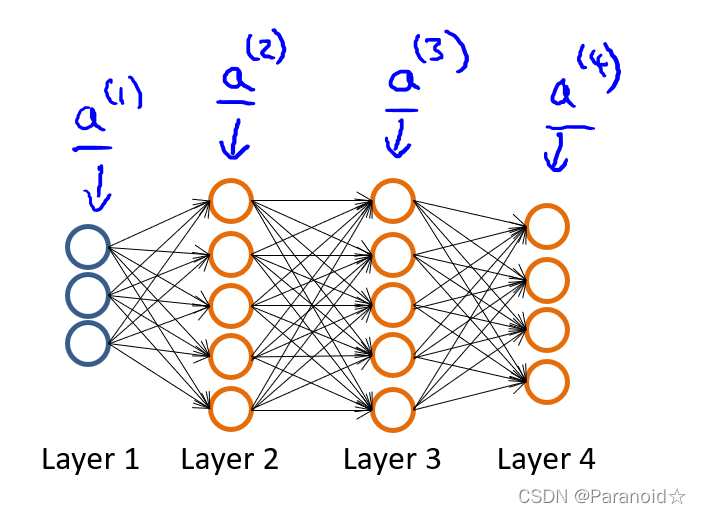
在这里插入图片描述
向前传播算法

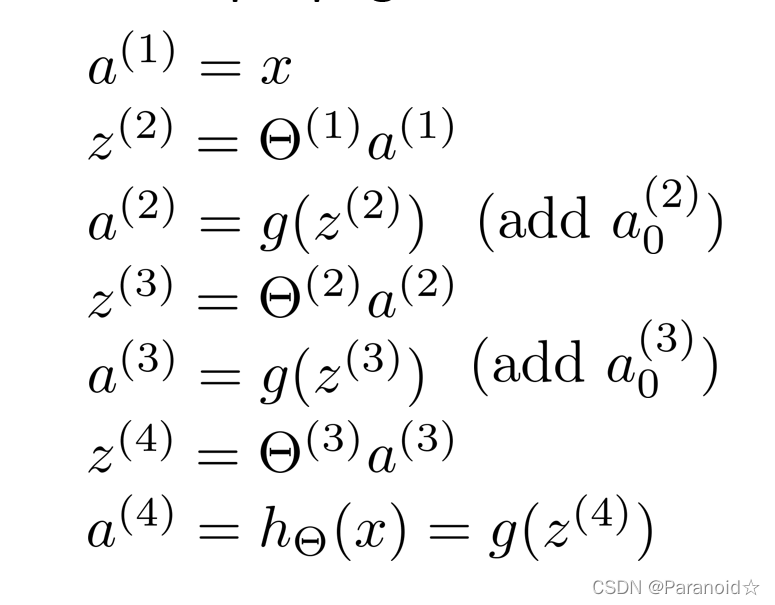
对于前向传播来说，不管维度多高，其过程都可以用如下公式表示

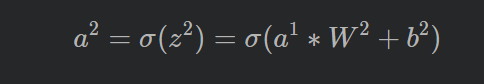
其中，上标代表层数，星号表示卷积，b表示偏置项bias，σ表示激活函数

Backpropagation Algorithm：从最后一层的误差开始计算，误差是激活单元的预测（ ak⁽⁴⁾ ）与实际值（ 𝑦^𝑘）之间的误差，（ 𝑘 = 1: 𝑘）

用𝛿来表示误差，则： 𝛿⁽⁴⁾ = 𝑎⁽⁴⁾ ? 𝑦，利用误差值来计算前一层的误差
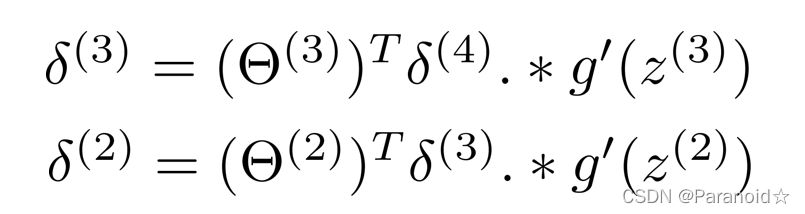
在这里插入图片描述
其中 𝑔′(𝑧⁽³⁾)是 𝑆 形函数的导数， 𝑔′(𝑧⁽³⁾) = 𝑎⁽³⁾ ? (1 ? 𝑎⁽³⁾),(𝜃⁽³⁾)𝑇𝛿⁽⁴⁾则是权重导致的误差的和

有了所有的误差的表达式后，便可以计算代价函数的偏导数了，假设𝜆 = 0，即不做任何正则化处理时有
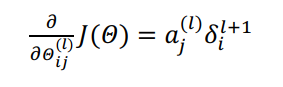
在这里插入图片描述

𝑙 代表目前所计算的是第几层
𝑗 代表目前计算层中的激活单元的下标，也将是下一层的第𝑗个输入变量的下标
𝑖 代表下一层中误差单元的下标，是受到权重矩阵中第𝑖行影响的下一层中的误差单元的下标

考虑正则化处理，并且训练集是一个特征矩阵而非向量，在上面的特殊情况中，需要计算每一层的误差单元来计算代价函数的偏导数，这里同样需要计算每一层的误差单元，但是需要为整个训练集计算误差单元，此时的误差单元也是一个矩阵，我们用𝛥𝑖𝑗^(𝑙)来表示这个误差矩阵：第 𝑙 层的第 𝑖 个激活单元受到第 𝑗个参数影响而导致的误差

算法大致过程
(1)首先用正向传播方法计算出每一层的激活单元，利用训练集的结果与神经网络预测的结果求出最后一层的误差，然后利用该误差运用反向传播法计算出直至第二层的所有误差
在这里插入图片描述
(2)计算代价函数的偏导数