[人工智能]Py-OpenCV学习记录5-滤波处理(一)

前言

滤波分为线性滤波和非线性滤波两种，线性滤波中有方框滤波、均值滤波和高斯滤波三种，非线性滤波则有中值滤波和双边滤波两种。在介绍滤波方式之前先以二维滤波的形式介绍滤波的运算。

滤波操作

二维滤波（二维卷积）

用二维滤波的方法选取不同的卷积核可以实现各种不同的效果，虽然OpenCV中内置函数能实现不同的操作，但是通过自己构建卷积核矩阵能够使我们更好的理解不同操作背后的运算逻辑。
将源图像和内核卷积处理，内核kernel（卷积核）是一个浮点数的矩阵，一个5×5的均值滤波内核矩阵如下所示，将内核（卷积核）的中心 与图像的一个像素对齐，5×5的内核则需要将中心周围的25个像素取平均值，并以此值替换中心的像素值，依次对整个图像的其他所有像素操作，便得到了滤波后的图像。
$$K=\frac{1}{9}?\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}?$$
首先介绍一下矩阵卷积的计算理论。
离散二维卷积公式：
$$B(i,j)=\sum _{m=0}\sum _{n=0}K(m.n)\times A(i?m,h?m)$$
其中A为被卷积矩阵、B为卷积结果、K为卷积内核。

$$A=?\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}?K=?\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}?$$
将卷积内核K翻转180°
$$\begin{gathered} K{ \\ }^{?}=?\begin{array}{ccc}9& 8& 7\\ 6& 5& 4\\ 3& 2& 1\end{array}? \end{gathered}$$
被卷积矩阵A拓展为 (m+2(n%2))x(m+2(n%2)) 的矩阵，在外围无元素位置以0填补
$$\begin{gathered} A{ \\ }^{?}=?\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 1& 2& 3& 0\\ 0& 4& 5& 6& 0\\ 0& 7& 8& 9& 0\\ 0& 0& 0& 0& 0\end{array}? \end{gathered}$$
将K*的中心依次对准A*的元素，相乘后相加
$$\begin{gathered} A{ \\ }^{?}=?\begin{array}{ccccc}0\times 9& 0\times 8& 0\times 7& 0& 0\\ 0\times 6& 1\times 5& 2\times 4& 3& 0\\ 0\times 3& 4\times 2& 5\times 1& 6& 0\\ 0& 7& 8& 9& 0\\ 0& 0& 0& 0& 0\end{array}? \end{gathered}$$
红色部分得出：0+0+0+0+5+8+0+8+5=26 为B(1,1)的值，依次对所有的元素计算，最终得出一个3x3的矩阵，便完成了矩阵的卷积运算。
结果为
$$\begin{gathered} K{ \\ }^{?}=?\begin{array}{ccc}26& 56& 54\\ 84& 155& 144\\ 134& 258& 186\end{array}? \end{gathered}$$
下面介绍函数
dst = cv2.filter2D(src, ddepth, kernel, dst=..., anchor=..., delta=..., borderType=...)

anchor 的取值会影响中心像素的位置，默认值(-1，-1)表示锚点位于内核中心。

import cv2
import numpy as np

#读取图片
im1 = cv2.resize(cv2.imread('cat1.jpg',0), None, fx=0.4, fy=0.4, interpolation=cv2.INTER_AREA)

#用Numpy生成了三个内核
#内核1为一个均值滤波的5x5的核
#内核2为一个3x3的边缘检测的核
#内核3为一个对对角线敏感的3x3的核
kernel1 = np.ones((5,5), np.float32)/25
kernel2 = np.mat('-1 -1 -1; -1 8 -1; -1 -1 -1', np.float32)
kernel3 = np.mat('-2 -1 0; -1 0 1; 0 1 2', np.float32)

#分别进行卷积运算
dst1 = cv2.filter2D(im1, -1, kernel1)
dst2 = cv2.filter2D(im1, -1, kernel2)
dst3 = cv2.filter2D(im1, -1, kernel3)

img = [im1, dst1, dst2, dst3]

for i in range(len(img)):
    cv2.imshow('Fig.'+str(i+1), img[i])

k = cv2.waitKey(0)
if k == ord('s'):
    cv2.destroyAllWindows() 

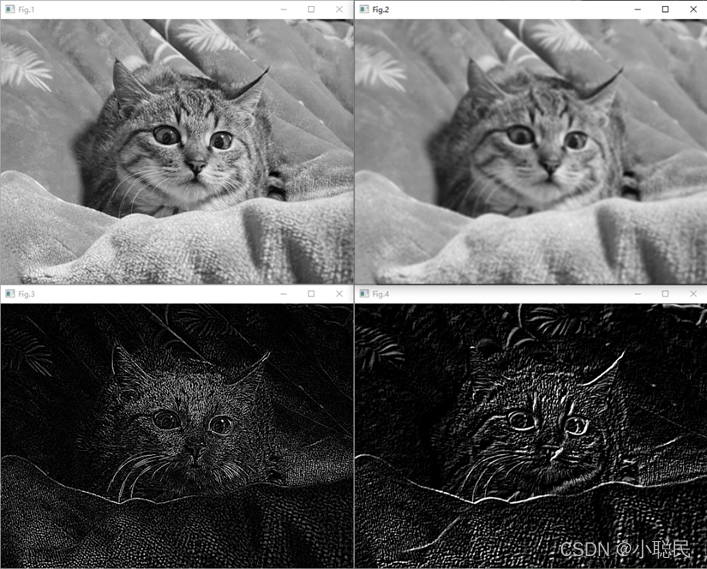
线性滤波

方框滤波/均值滤波

这是最简单的一种滤波方式，方框滤波/均值滤波的作用是模糊一张图片。
使用的是 cv2.boxFilter() 方框滤波和 cv2.blur() 均值滤波
卷积核如下所示
$$Kernal=\alpha ?\begin{array}{cccc}1& 1& ...& 1\\ 1& 1& ...& 1\\ ...& ...& & \\ 1& 1& & 1\end{array}?$$
$$\alpha =\{\begin{array}{ll}\frac{1}{ksize\times ksize}& \text{,?}normalize=True\\ 1& \text{,?}normalize=False\end{array}$$
当方框滤波的参数 normalize 为 True 时，方框滤波的内核和均值滤波的内核相同。
dst=cv.boxFilter(src, ddepth, ksize[, dst[, anchor[, normalize[, borderType]]]])

dst=cv.blur(src, ksize[, dst[, anchor[, borderType]]])

import cv2
import numpy as np

#读取图片
im1 = cv2.resize(cv2.imread('cat1.jpg',1), None, fx=0.4, fy=0.4, interpolation=cv2.INTER_AREA)
#生成内核卷积与OpenCV的均值模糊相对比
kernal_1 = np.ones((5,5), np.float32)/25

#分别进行卷积运算
dst1 = cv2.blur(im1, (5,5))
dst2 = cv2.boxFilter(im1, -1, (5,5))
dst3 = cv2.filter2D(im1, -1, kernal_1)

img = [im1, dst1, dst2, dst3]

for i in range(len(img)):
    cv2.imshow('Fig.'+str(i+1), img[i])

k = cv2.waitKey(0)
if k == ord('s'):
    cv2.destroyAllWindows() 

高斯滤波

高斯滤波是一种线性平滑滤波，用来消除高斯噪声效果极佳，通常用于图像的降噪。高斯滤波的卷积运算是一个加权平均的计算过程，其权函数来自正态分布函数，其本质便是图像与正态分布做卷积运算，正态分布也叫高斯分布，因此得名高斯滤波/高斯模糊。
高斯滤波是图像处理中十分常用的一种滤波技术，处理的效果好但是效率并不高。由于高斯函数的傅里叶变换后任为高斯函数，只是幅度和方差发生了变化，所以高斯滤波对于图像来说也是一种低通滤波操作。
一维高斯函数如下：
$$\begin{gathered} G(x)=\alpha e{ \\ }^{?\frac{(i?(\frac{ksize?1}{2})){ \\ }^2}{2\sigma { \\ }^2}} \end{gathered}$$
其中
i 为满足 0<=i<=ksize-1 的整数
α 为使得 ∑G = 1 的一个值
ksize 为卷积核的阶数（长度）
σ 为标准差，通常取1其值越大表示周围的像素点权重越大，也可由下式计算得
$$\sigma =0.3\times (\frac{ksize?1}{2}?1)+0.8$$
例如
当卷积核阶数为3时，即 ksize = 3 ，那么 i = 0,1,2
取 σ=1
则有 G’₁=[0.60653 1 0.60653]
通过计算可得
$$\begin{gathered} a=\frac{1}{\Sigma G{ \\ }_i}=\frac{1}{2.21306}=0.45186 \end{gathered}$$
最终得出 G₁=[0.27410 0.45186 0.27410]
此时得出的为一维的高斯权值
计算二维得高斯模板可以通过 G^TG 计算
得：
$$\begin{gathered} G{ \\ }^{T}G=?\begin{array}{ccc}0.0751& 0.1239& 0.0751\\ 0.1239& 0.2047& 0.1239\\ 0.0751& 0.1239& 0.0751\end{array}? \end{gathered}$$
在OpenCV中也可以通过 cv2.getGaussianKernal() 来创造高斯卷积核。
dst=cv2.GaussianBlur(src, ksize, sigmaX[, dst[, sigmaY[, borderType]]])

import cv2
import numpy as np
#读取图片
im1 = cv2.resize(cv2.imread('cat1.jpg',1), None, fx=0.4, fy=0.4, interpolation=cv2.INTER_AREA)

#生成5x5的高斯内核与OpenCV的高斯模糊相对比
kernal_1 = np.mat('0.00297 0.01331 0.02194 0.01331 0.00297;\
                    0.01331 0.05963 0.09832 0.05963 0.01331;\
                    0.02194 0.09832 0.16210 0.09832 0.02194;\
                    0.01331 0.05963 0.09832 0.05963 0.01331;\
                    0.00297 0.01331 0.02194 0.01331 0.00297', np.float32)

#分别进行卷积运算
dst1 = cv2.GaussianBlur(im1, (5,5), 1)
#dst2 = cv2.GaussianBlur(im1, (5,5), 0.1)
#dst3 = cv2.GaussianBlur(im1, (5,5), 100)
dst2 = cv2.filter2D(im1, -1, kernal_1)

img = [im1, dst1, dst2]

for i in range(len(img)):
    cv2.imshow('Fig.'+str(i+1), img[i])

k = cv2.waitKey(0)
if k == ord('s'):
    cv2.destroyAllWindows() 

代码及结果如下所示，完全相同！

最后祝大家学习顺利噢！