[人工智能]数值计算之 拟牛顿法

前言

无论是牛顿法，高斯牛顿法，还是LM算法，都需要计算海森矩阵或其近似，然后求海森矩阵的逆，来获得迭代增量，因此存在迭代不收敛问题（海森矩阵的正定性），并且计算效率较低。

拟牛顿法更进一步，将海森矩阵也作为一个迭代估计量，因而避免了海森矩阵的求逆运算，并提升了迭代稳定性。

拟牛顿条件

仍然是从优化函数的泰勒展开讲起：
$$\begin{gathered} f(\mathbf{x})=f({\mathbf{x}}_{\mathbf{k}})+?f({\mathbf{x}}_{\mathbf{k}}{)}^T(\mathbf{x}?{\mathbf{x}}_{\mathbf{k}})+\frac{1}{2}(\mathbf{x}?{\mathbf{x}}_{\mathbf{k}}{)}^{T}H({\mathbf{x}}_{\mathbf{k}})(\mathbf{x}?{\mathbf{x}}_{\mathbf{k}}) \\ ?f(\mathbf{x}{)}^T=?f({\mathbf{x}}_{\mathbf{k}}{)}^T+H({\mathbf{x}}_{\mathbf{k}})(\mathbf{x}?{\mathbf{x}}_{\mathbf{k}}) \end{gathered}$$
简写为：
$$J(\mathbf{x})?J({\mathbf{x}}_{\mathbf{k}})=H({\mathbf{x}}_{\mathbf{k}})(\mathbf{x}?{\mathbf{x}}_{\mathbf{k}})$$
假设我们通过$J(\mathbf{x})=0$求出了本次迭代增量$\Delta \mathbf{x}$，现在将$\mathbf{x}={\mathbf{x}}_{\mathbf{k}+1}={\mathbf{x}}_{\mathbf{k}}+\Delta \mathbf{x}$代入：
$$J({\mathbf{x}}_{\mathbf{k}+1})?J({\mathbf{x}}_{\mathbf{k}})=H({\mathbf{x}}_{\mathbf{k}})({\mathbf{x}}_{\mathbf{k}+1}?{\mathbf{x}}_{\mathbf{k}})(1?1)$$
如果我们要通过迭代$G_{k+1}$近似$H(x_k{)}^{?1}$，那么$G_k$也要满足以上方程。这就是拟牛顿条件：
$$\begin{gathered} G_{k+1}(J_{k+1}?J_k)=({\mathbf{x}}_{\mathbf{k}+1}?{\mathbf{x}}_{\mathbf{k}}) \\ set{J}_{k+1}?J_k=y_k,({\mathbf{x}}_{\mathbf{k}+1}?{\mathbf{x}}_{\mathbf{k}})=s_k \\ then{G}_{k+1}{y}_k=s_k(2) \\ and{y}_k=G_{k+1}^{?1}{s}_k(3) \end{gathered}$$
注意：用${\mathbf{x}}_{\mathbf{k}+1},J_{k+1}$迭代$G_{k+1}$似乎只能近似第$k$次迭代的海森矩阵$H({\mathbf{x}}_{\mathbf{k}})$。不过实际上，如果把式(1-1)改写为以下形式：
$$\begin{gathered} J({\mathbf{x}}_{\mathbf{k}?1})?J({\mathbf{x}}_{\mathbf{k}})=H({\mathbf{x}}_{\mathbf{k}})({\mathbf{x}}_{\mathbf{k}?1}?{\mathbf{x}}_{\mathbf{k}})(1?2) \\ \to J({\mathbf{x}}_{\mathbf{k}})?J({\mathbf{x}}_{\mathbf{k}?1})=H({\mathbf{x}}_{\mathbf{k}})({\mathbf{x}}_{\mathbf{k}}?{\mathbf{x}}_{\mathbf{k}?1}) \\ \to J({\mathbf{x}}_{\mathbf{k}+1})?J({\mathbf{x}}_{\mathbf{k}})=H({\mathbf{x}}_{\mathbf{k}+1})({\mathbf{x}}_{\mathbf{k}+1}?{\mathbf{x}}_{\mathbf{k}}) \end{gathered}$$
这样，$G_{k+1}$就是$H({\mathbf{x}}_{\mathbf{k}+1})$的近似了。

几何解释

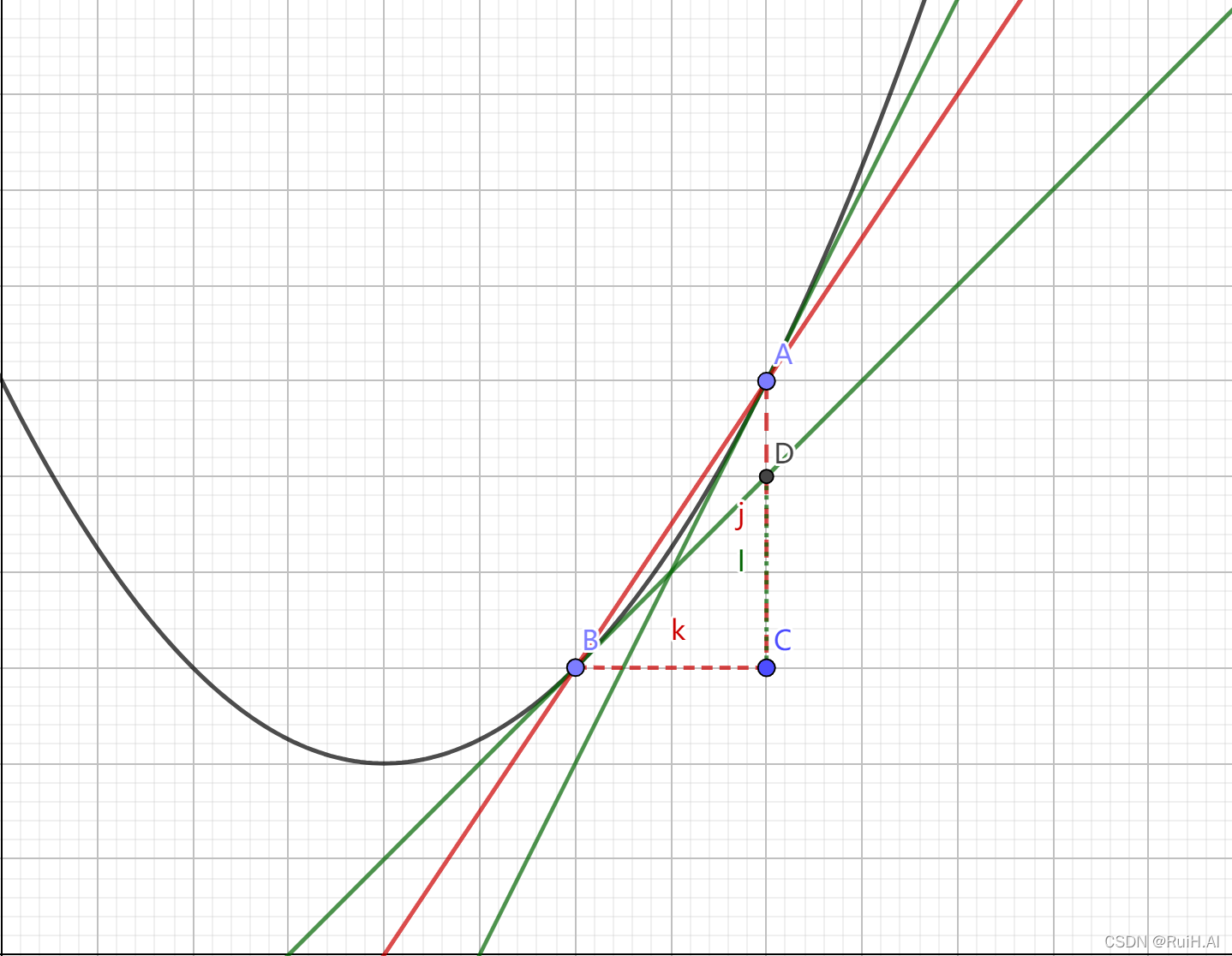
用一元函数来理解更简单，如下图，黑色线是优化函数的一阶导，$A,B$点是$x_k,x_{k+1}$，拟牛顿法的思想就是通过红色割线$AB$的斜率来近似$B$点的二阶导（也就是B点的切线，绿线）；另一方面，红色切线对于$A$点的切线也能近似，这就是式(1-1),(1-2)的几何意义。

DFP算法

DFP算法（DFP是人名）通过迭代构造$G_k$来近似$H_k^{?1}$。DFP公式推导如下：
$$\begin{gathered} G_{k+1}=G_k+P_k+Q_k \\ {G}_{k+1}{y}_k=s_k\to G_k{y}_k+P_k{y}_k+Q_k{y}_k=s_k \\ set{P}_k{y}_k=s_k,Q_k{y}_k=?G_k{y}_k \\ then{P}_k=\frac{s_k{s}_k^T}{s_k^T{y}_k},Q_k=?\frac{G_k{y}_k{y}_k^T{G}_k}{y_k^T{G}_k{y}_k} \\ {G}_{k+1}=G_k+\frac{s_k{s}_k^T}{s_k^T{y}_k}?\frac{G_k{y}_k{y}_k^T{G}_k}{y_k^T{G}_k{y}_k} \end{gathered}$$

DFP算法中，当初始$G$正定时，迭代中的每个$G$都是正定的。

BFGS算法

BFGS算法（BFGS是四位作者的首字母）通过构造$B_k$来近似$H_k$，推导方式与DFP算法相似：
$$\begin{gathered} B_{k+1}=B_k+P_k+Q_k \\ {B}_{k+1}{s}_k=y_k\to B_k{s}_k+P_k{s}_k+Q_k{s}_k=y_k \\ set{P}_k{s}_k=y_k,Q_k{s}_k=?B_k{s}_k \\ then{P}_k=\frac{y_k{y}_k^T}{y_k^T{s}_k},Q_k=?\frac{B_k{s}_k{s}_k^T{B}_k}{s_k^T{B}_k{s}_k} \\ {B}_{k+1}=B_k+\frac{y_k{y}_k^T}{y_k^T{s}_k}?\frac{B_k{s}_k{s}_k^T{B}_k}{s_k^T{B}_k{s}_k} \end{gathered}$$
BFGS算法中，当初始$B$正定时，迭代中的每个$B$都是正定的。

注意：由于原BFGS算法没有直接近似海森矩阵的逆，因此可以进一步应用Sherman-Morrison-Woodbury公式直接从$B_k^{?1}$得到$B_{k+1}^{?1}$。由于这个公式我还不大熟，因此这里给出结果，以后有时间再记录推导细节：
$$B_{k+1}^{?1}=(I?\frac{s_k{y}_k^T}{y_k^T{s}_k})B_k^{?1}(I?\frac{y_k{s}_k^T}{y_k^T{s}_k})+\frac{s_k{s}_k^T}{y_k^T{s}_k}$$

Broyden类算法

上面的DFP和BFGS都能得到$H_k^{?1}$的迭代近似$G_{k?DFP},G_{k?BFGS}$，那么DFP和BFGS迭代的线性组合也满足拟牛顿条件，并且迭代保持正定：
$$G_k=\lambda G_{k?DFP}+(1?\lambda )G_{k?BFGS},0\le \lambda \le 1$$
这被称为Broyden类算法。

代码示例

下面是我写的通过拟牛顿法DFP求二元函数极小值的python代码：

import numpy as np
import scipy.optimize
import time
import math


def partial_derivate_xy(x, y, F):
    dx = (F(x + 0.001, y) - F(x, y))/0.001
    dy = (F(x, y + 0.001) - F(x, y))/0.001
    return dx, dy


def partial_partial_derivate_xy(x, y, F):
    dx, dy = partial_derivate_xy(x, y, F)
    dxx = (partial_derivate_xy(x + 0.001, y, F)[0] - dx) / 0.001
    dyy = (partial_derivate_xy(x, y + 0.001, F)[1] - dy) / 0.001
    dxy = (partial_derivate_xy(x, y + 0.001, F)[0] - dx) / 0.001
    dyx = (partial_derivate_xy(x + 0.001, y, F)[1] - dy) / 0.001
    return dxx, dyy, dxy, dyx


def non_linear_func(x, y):
    fxy = 0.5 * (x ** 2 + y ** 2)
    return fxy


def non_linear_func_2(x, y):
    fxy = x*x + 2*y*y + 2*x*y + 3*x - y - 2
    return fxy


def non_linear_func_3(x, y):
    fxy = 0.5 * (x ** 2 - y ** 2)
    return fxy


def non_linear_func_4(x, y):
    fxy = x**4 + 2*y**4 + 3*x**2*y**2 + 4*x*y**2 + x*y + x + 2*y + 0.5
    return fxy


def non_linear_func_5(x, y):
    fxy = math.pow(math.exp(x) + math.exp(0.5 * y) + x, 2)
    return fxy


def quasi_newton_optim(x, y, F, G, lr=0.1):
    dx, dy = partial_derivate_xy(x, y, F)
    grad = np.array([[dx], [dy]])

    vec_delta = - lr * np.matmul(G, grad)
    vec_opt = np.array([[x], [y]]) + vec_delta
    x_opt = vec_opt[0][0]
    y_opt = vec_opt[1][0]

    dxx, dyy = partial_derivate_xy(x_opt, y_opt, F)
    grad_delta = np.array([[dxx - dx], [dyy - dy]])
    G_update = G + np.matmul(vec_delta, vec_delta.T)/np.dot(vec_delta.T, grad_delta) \
                - np.matmul(np.matmul(np.matmul(G, grad_delta), grad_delta.T), G) / np.matmul(np.matmul(grad_delta.T, G), grad_delta)

    return x_opt, y_opt, grad, G_update


def quasi_newton_optim_correct(x, y, F, G):
    dx, dy = partial_derivate_xy(x, y, F)
    grad = np.array([[dx], [dy]])

    vec_delta = - np.matmul(G, grad)
    vec_opt = np.array([[x], [y]]) + vec_delta
    x_opt = vec_opt[0][0]
    y_opt = vec_opt[1][0]

    dxx, dyy = partial_derivate_xy(x_opt, y_opt, F)
    grad_delta = np.array([[dxx - dx], [dyy - dy]])
    Gy = np.matmul(G, grad_delta)
    yG = np.matmul(grad_delta.T, G)
    yGy = np.matmul(np.matmul(grad_delta.T, G), grad_delta)
    G_update = G + np.matmul(vec_delta, vec_delta.T)/np.dot(vec_delta.T, grad_delta) \
                - np.matmul(Gy, yG) / yGy

    return x_opt, y_opt, grad, G_update


def optimizer(x0, y0, F, th=0.01):
    x = x0
    y = y0
    G = np.eye(2)

    counter = 0
    while True:
        x_opt, y_opt, grad, G = quasi_newton_optim(x, y, F, G)
        if np.linalg.norm(grad) < th:
            break
        x = x_opt
        y = y_opt
        counter = counter + 1
        print('iter: {}'.format(counter), 'optimized (x, y) = ({}, {})'.format(x, y))
    return x, y


def verify_min(x, y, F):
    fx = F(x, y)
    deltax = np.linspace(-0.1, 0.1, 100)
    deltay = np.linspace(-0.1, 0.1, 100)
    x_range = x + deltax
    y_range = y + deltay
    counter = 0
    for i in range(100):
        for j in range(100):
            f_range = F(x_range[i], y_range[j])
            f_delta = fx - f_range
            if f_delta < 0:
                counter += 1

    print('counter: {}'.format(counter))


def scipyF(X):
    x, y = X
    fxy = x ** 4 + 2 * y ** 4 + 3 * x ** 2 * y ** 2 + 4 * x * y ** 2 + x * y + x + 2 * y + 0.5
    return fxy


if __name__ == '__main__':
    x0 = 2.
    y0 = 2.
    start = time.time()
    for i in range(1000):
        result_x, result_y = optimizer(x0, y0, non_linear_func_5)
        if i == 0:
            break
    end = time.time()
    print(result_x, result_y, 'cost time: {}'.format(end - start))
    print(partial_derivate_xy(result_x, result_y, non_linear_func_5))
    verify_min(result_x, result_y, non_linear_func_5)

    # scipyRes = scipy.optimize.fmin_cg(scipyF, np.array([0, 0]))
    # print(scipyRes)

后记

牛顿法与拟牛顿法只剩一个LBFGS算法了。为了加深印象和实际应用，下一篇LBFGS我会把这一块的代码做成一个类来使用，并且添加可视化结果。