语义分割中的评价指标问题
语义分割归根结底就是像素级别的二分类/多分类问题。在测试评价的时候用到各种评价指标,网上很多人的总结要么太凌乱,甚至还有错误,总结一下各种常用的评价指标,以备使用时查阅,如有错误欢迎指出。
1.二分类与多分类TP,TN,FP,FN
1).二分类
- TP:标签值为正样本,预测值也为正样本
- TN:标签值为负样本,预测值也为负样本
- FP:标签值为负样本,预测值为正样本
- FN:标签值为正样本,预测值为负样本
所以要注意的是:标签值中的
P=TP+FN, N =TN+FN

图片引用于二分类
2). 多分类
多分类问题中的TP\TN\FP\TN这些指标要具体和某一类挂钩。举个例子,如果有一个多分类(类别为5),下面是求类别为4的各项参数:
- TP:标签值类别为4,预测值类别也为4
- TN:标签值与预测值保持一致,值为1、2、3、5中的任何一个
- FP:标签值类别为4,预测值类别为1、2、3、5中的任何一个
- FN:标签值类别为1、2、3、5,预测值类别为4
以上就是关于类别4的TP、TN、FP、FN解释。下面是多分类的混淆矩阵。混淆矩阵求法可以看第二部分。

图片引用于多分类
2.多分类混淆矩阵介绍与代码
在第一部分介绍了多分类和二分类的基础指标问题。这部分介绍混淆矩阵。混淆矩阵的定义:
混淆矩阵是机器学习中总结分类模型预测结果的情形分析表,以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。一般来说矩阵的行表示真实值,矩阵的列表示预测值。
混淆矩阵代码实现有多种方式,本文介绍两种。
2.1通过sklean库实现
官方文档here
语法实现:
from sklearn.metrics import confusion_matrix
confusion_matrix参数:
y_true :一维数组。维度shape = [n_samples]
y_pred:一维数组。维度shape = [n_samples]
labels:array类型, 维度shape = [n_classes](这个的作用笔者实验了下,就是等于求某类的TP)
sample_weight:样本权重(一般用不上)
根据以上所述,confusion_matrix函数接受单通道的预测值和单通道的标签值。所以一般经过argmax操作再flatten之后传入。
消融比较:
1.预测值或标签值包含全部的类别
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]], dtype=int64)
2.预测值和标签值不包含全部的类别
>>> y_true = [3, 0, 3, 3, 0, 1]
>>> y_pred = [0, 0, 3, 3, 0, 3]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]], dtype=int64)
综上消融所述:
基于sklearn库求的混淆矩阵,只包含传入类别的,不按照实际标签值,容易忽略,不适合求多张图片混淆矩阵叠加。
2.2 通过numpy实现
实现语法:
>>>def Hist(y_true,y_pred,numclass):
>>> hist=np.bincount(numclass * y_true.astype(int)+y_pred,minlength=numclass ** 2).reshape(numclass, numclass)
>>> return hist
如果一个图片有n类,直接建立一个n*n混淆矩阵。
消融比较:
1.
>>>y_true = np.array([2, 0, 2, 2, 0, 1])
>>>y_pred = np.array([0, 0, 2, 2, 0, 2])
>>>numclass = 4
>>>Hist(y_true,y_pred,numclass)
array([[2, 0, 0, 0],
[0, 0, 1, 0],
[1, 0, 2, 0],
[0, 0, 0, 0]], dtype=int64)
2.
>>>y_true = np.array([3, 0, 3, 3, 0, 1])
>>>y_pred = np.array([0, 0, 3, 3, 0, 3])
>>>numclass = 4
>>>Hist(y_true,y_pred,numclass)
array([[2, 0, 0, 0],
[0, 0, 0, 1],
[0, 0, 0, 0],
[1, 0, 0, 2]], dtype=int64)
综上所述:自己编写的代码是建立完整的混淆矩阵,而不是根据传入的类的种类数目来建立。
3.F1-score介绍与代码
F1-score的定义如下:
F1分数(F1 Score):是统计学中用来衡量二分类模型精确度的一种指标。 它同时兼顾了分类模型的精确率和 召回率 。 F1分数可以看作是模型精确率和 召回率 的一种调和平均,它的最大值是1,最小值是0。 分数( Score),又称平衡F分数(balanced F Score),它被定义为精确率和 召回率 的 调和平均数 。
准确率( P ):
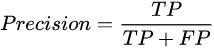
召回率( R ) :
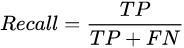
F1-score :
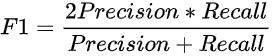
经过化简:
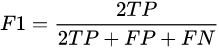
3.1通过sklean库实现F1-score
实现语法:
sklearn.metrics.f1_score(y_true,
y_pred,
labels=None,
pos_label=1,
average=’binary’,
sample_weight=None)
f1_score参数:
y_true :一维数组。维度shape = [n_samples]
y_pred:一维数组。维度shape = [n_samples]
average:string, [None, ‘binary’ (default), ‘micro’, ‘macro’, ‘weighted’, ‘samples’],有这六个中取值,意义如下
- None:返回每一类各自的f1_score,得到一个array.
- == ‘binary’==:只对二分类问题有效,返回由pos_label指定的类的f1_score。
- ‘micro’:设置average='micro’时,Precision = Recall = F1_score = Accuracy。整体计算TP,FN,FP
- == ‘macro’==:对每一类别的f1_score进行简单算术平均(unweighted mean),这类有一个前提假设:每一个类都同等的重要。
- == ‘weighted’==:对每一类别的f1_score进行加权平均,权重为各类别数在y_true中所占比例。
- ‘samples’:用于多标签任务,按照样本维度计算混淆矩阵,然后计算平均值。(笔者实验后发现这个必须有规定形式,标签值和预测值必须是独热编码)
sample_weight:(一般用不上)
消融对比:
举个例子:
标签值:[0, 0, 0, 0, 1, 1, 1, 2, 2]
预测值:[0, 0, 1, 2, 1, 1, 2, 1, 2]
可以得出这个混淆矩阵为:
2 1 1
0 2 1
0 1 1
也可以的出来:
0类:TP=2,FP=0,FN=2
1类:TP=2,FP=2,FN=1
2类:TP=1,FP=2,FN=1 怎么求我就不过多赘述了
0类别的准确率 : PA = 2/(2+0)= 1
0类别的召回率 : RA = 2/(2+2)= 0.5
0类别的F1-score : FA = 2*(1*0.5)/(1+0.5) = 0.667
1类别的准确率 : PB = 2/(2+2)= 0.5
1类别的召回率 : RB = 2/(2+1)= 0.667
1类别的F1-score : FB = 2*(0.5*0.667)/(0.5+0.667) = 0.572
2类别的准确率 : PC = 1/(1+2)= 0.333
2类别的召回率 : RC = 1/(1+1)= 0.5
2类别的F1-score : FC = 2*(0.333*0.5)/(0.333+0.5) = 0.39976
所有数据的F1-score:
有两种方式
第一种方式是计算数据中所有的TP,FP,FN,然后计算F1-score,即micro;
第二种方式是分别计算各个类别的TP,FP,FN,然后计算各个类被的F1-score,然后对F-score求平均,即macro.
micro:
P = 5/(5+4) = 0.556
R = 5/(5+4) = 0.556
F1-score = 2*(0.556*0.556)/(0.556+0.556) = 0.556
macro :
F1-score = (0.667+0.572+0.39976)/3 = 0.5462
代码实现:
>>>from sklearn.metrics import f1_score
>>>y_true = [0, 0, 0, 0, 1, 1, 1, 2, 2]
>>>y_pred = [0, 0, 1, 2, 1, 1, 2, 1, 2]
>>>f1_micro = f1_score(y_true,y_pred,average='micro')
0.5555555555555556
>>>f1_macro = f1_score(y_true,y_pred,average='macro')
0.546031746031746
>>>f1_None = f1_score(y_true,y_pred,average=None)
array([0.66666667, 0.57142857, 0.4 ])
>>>z1= np.eye(3)[np.array(y_true ).reshape(-1)] # 独热编码
>>>z2=np.eye(3)[np.array(y_pred ).reshape(-1)] # 独热编码
>>>f1_score=(z1,z2,average="samples") #这个测试处于micro与macro之间,笔者不建议使用
0.5555555555555556
3.2 numpy来实现F1-score
不太建议,比较复杂,而且会让值虚高,训练可以尝试使用,测试还是建议使用sklearn库自带的。这个是直接通过求TP,FP,FN,TN来进行测试。但是为了避免出现NaN数值,这里面求F1分数的时候通过分子分母同加一个极小值。但是!这样会造成一个小后果:假设在k类,预测和标签都没有的情况下,关于k类的F1就会变成1。然后这个最后求平均F1score就会导致值虚高。
def f_score(inputs, target, beta=1, smooth = 1e-5, threhold = 0.5):
n, c, h, w = inputs.size()
nt, ht, wt, ct = target.size()
if h != ht and w != wt:
inputs = F.interpolate(inputs, size=(ht, wt), mode="bilinear", align_corners=True)
temp_inputs = torch.softmax(inputs.transpose(1, 2).transpose(2, 3).contiguous().view(n, -1, c),-1)
temp_target = target.view(n, -1, ct)
#--------------------------------------------#
# 计算dice系数
#--------------------------------------------#
temp_inputs = torch.gt(temp_inputs,threhold).float()
tp = torch.sum(temp_target * temp_inputs, axis=[0,1])
fp = torch.sum(temp_inputs , axis=[0,1]) - tp
fn = torch.sum(temp_target , axis=[0,1]) - tp
score = ((1 + beta ** 2) * tp + smooth) / ((1 + beta ** 2) * tp + beta ** 2 * fn + fp + smooth)
score = torch.mean(score)
return score
4.多分类的MIoU和IoU介绍与代码
Mean Intersection over Union(MIoU,均交并比)为语义分割的标准度量。 其计算两个集合的交集和并集之比,在语义分割问题中,这两个集合为真实值(ground truth)和预测值(predicted segmentation)。
IoU(Intersection over Union)IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值.
IoU是求得单个类,而MIoU求得是所有类平均。
公式如下:
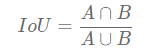
在多分类情况下,B是代表除了A之外得所有类。

简化成TP、TF、FN、FP公式:
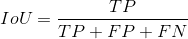
代码实现:
1.通过混淆矩阵来求每类得IOU,这个函数传入一个n*n的混淆矩阵,返回一个[n]数组(反映每一类的Iou)
如果想再求MIoU,直接进行 np.nanmean(hist) 就可以了。
# 为什么不用np.mean()? 因为一张图中有些类标签值没有,预测值没有,就会出现0/0=Nan情况
>>>def per_class_iu(hist):
>>> return np.diag(hist) / np.maximum((hist.sum(1) + hist.sum(0) - np.diag(hist)), 1)
# hist.sum(0) 是压缩成一行 求的是什么呢 TP+FN TP:标签为1 预测为1的个数 FN 标签为1 预测为其他的 就是FN
# hist.sum(1) 是压缩成一列 求的是什么呢 TP+FP TP:标签为1 预测为1的个数 FN 标签为其他 预测为1的 就是FP