[人工智能]机器学习-线性回归

线性回归

线性回归作为机器学习入门时候所学习的第一门课，结构简单，原理清晰。因此往往容易被学习者所忽视，其实线性回归虽然简单，但是确实一套具有很高的实战价值的算法，在很多的现实场景中有着非常广泛的应用。

线性回归模型

线性回归总结起来就是两个字：拟合，也就是通过调整直线方程的参数，使得所作直线拟合数据集点，从而达到趋近于理论点的过程。
线性回归的模型定义为：

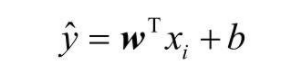
代码实现

import numpy as np
import matplotlib.pyplot as plt 

def true_fun(X): # 这是我们设定的真实函数，即ground truth的模型
    return 1.5*X + 0.2

np.random.seed(0) # 设置随机种子
n_samples = 30 # 设置采样数据点的个数

'''生成随机数据作为训练集，并且加一些噪声'''
X_train = np.sort(np.random.rand(n_samples)) 
y_train = (true_fun(X_train) + np.random.randn(n_samples) * 0.05).reshape(n_samples,1)

from sklearn.linear_model import LinearRegression # 导入线性回归模型
model = LinearRegression() # 定义模型
model.fit(X_train[:,np.newaxis], y_train) # 训练模型
print("输出参数w：",model.coef_) # 输出模型参数w
print("输出参数b：",model.intercept_) # 输出参数b

通过运行模型并输出模型参数可以看到，线性回归拟合的参数是1.44和0.22，很接近实际的1.5和0.2，说明我们的算法性能还不错。

X_test = np.linspace(0, 1, 100)
plt.plot(X_test, model.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="True function")
plt.scatter(X_train,y_train) # 画出训练集的点
plt.legend(loc="best")
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures # 导入能够计算多项式特征的类
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

def true_fun(X): # 这是我们设定的真实函数，即ground truth的模型
    return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30 # 设置随机种子

X = np.sort(np.random.rand(n_samples)) 
y = true_fun(X) + np.random.randn(n_samples) * 0.1

degrees = [1, 4, 15] # 多项式最高次
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
    ax = plt.subplot(1, len(degrees), i + 1)
    plt.setp(ax, xticks=(), yticks=())
    polynomial_features = PolynomialFeatures(degree=degrees[i],
                                             include_bias=False)
    linear_regression = LinearRegression()
    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression)]) # 使用pipline串联模型
    pipeline.fit(X[:, np.newaxis], y)
    
    scores = cross_val_score(pipeline, X[:, np.newaxis], y,scoring="neg_mean_squared_error", cv=10) # 使用交叉验证
    X_test = np.linspace(0, 1, 100)
    plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
    plt.plot(X_test, true_fun(X_test), label="True function")
    plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.xlim((0, 1))
    plt.ylim((-2, 2))
    plt.legend(loc="best")
    plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
        degrees[i], -scores.mean(), scores.std()))
plt.show()