1.例题:(第一个式子里的cos2.4π掉了一个π)

?求解问题:使用精确插值方法,并确定 RBFN 的权重。假设 RBF 是标准差为 0.1 的高斯函数。使用测试集评估得到的 RBFN 的近似性能
2.解题思路
径向基函数插值的关键点在于径向基函数的选择和利用训练数据求解权重w。
? ? ? ? ? ? ?
? ? ? ? ??
3.代码实现
题目要求我们使用的RBF(径向基函数)是标准差为 0.1 的高斯函数:(宽度参数为0.1)?

首先是根据题目要求获取训练集和测试集数据:
# 获取所需数据
def get_data(x1,x2):
mu = 0
sigma = 1
n = []
for i in range(len(x1)):
n.append(random.gauss(mu, sigma))
y_train = 1.2*(np.sin(np.pi*x1))-np.cos(2.4*np.pi*x1)+0.3 * np.array(n) # 训练集加上了正态分布干扰项n
y_test = 1.2*(np.sin(np.pi*x2))-np.cos(2.4*np.pi*x2)
return y_train, y_testsnum = 41 # control point数量
ratio = 5 # 总数据点数量:snum*ratio
sig = 0.1 # 核函数标准差(宽度参数)
xs = -1
xe = 1
x_train = np.linspace(xs, xe, snum) # 训练集
x_test = np.linspace(xs, xe, (snum-1)*ratio+1) # 测试集
y_train, y_test = get_data(x_train, x_test)得到数据于是根据选取的中心点与训练集数据定义函数求解权重w:
# 求解权重w
def kernel_interpolation(y_train,x_train,sig):
gaussian_kernel = lambda x,c,h: np.exp(-(x-x[c])**2/(2*(h**2)))
num = len(y_train)
w = np.zeros(num)
int_matrix = np.asmatrix(np.zeros((num,num)))
for i in range(num):
int_matrix[i,:] = gaussian_kernel(x_train,i,sig)
w = int_matrix.I * np.asmatrix(y_train).T
return w接着定义函数使用测试集与中心点求和计算进行插值拟合:
# 求解插值拟合点
def kernel_interpolation_rec(w,x_center,x_test,sig):
kernel = lambda x,xc,h: np.exp(-(x-xc)**2/(2*(h**2)))
num = len(x_test)
y_rec = np.zeros(num)
for i in range(num):
for k in range(len(w)):
y_rec[i] = y_rec[i] + w[k]*kernel(x_test[i],x_center[k],sig)
return y_rec?然后绘制插值图像:
plt.figure(1)
w = kernel_interpolation(y_train, x_train, sig) # 解出权重
y_rec = kernel_interpolation_rec(w, x_train, x_test, sig) # 求解拟合曲线点
plt.plot(x_test,y_rec,'k')
plt.plot(x_test,y_test,'r:')
# plt.plot(x2,y_all,'k:')
plt.ylabel('y')
plt.xlabel('x')
for i in range(len(x_train)):
plt.plot(x_train[i],y_train[i],'go',markerfacecolor='none')
plt.legend(labels=['reconstruction','original','control point'],loc='best')
plt.title('kernel interpolation:$y=1.2sin(\pi x)+cos(2.4\pi x)$')
plt.show()输出图像结果如下:

最后评估得到的 RBFN 的近似性能,评估指标很多种,这里主要介绍MAE(平均绝对误差),MSE(均方误差):?
1.平均绝对误差(Mean Absolute Error)指的就是模型预测值 f(x) 与样本真实值 y 之间距离的平均值。其公式如下所示:

mae损失函数图像:
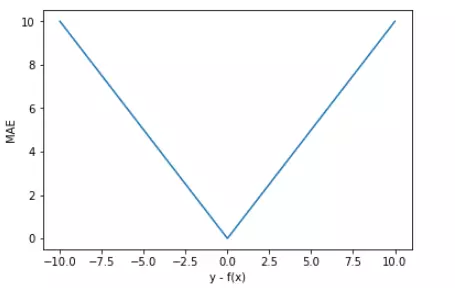
????????直观上来看,MAE 的曲线呈 V 字型,连续但在 y-f(x)=0 处不可导,计算机求解导数比较困难。而且 MAE 大部分情况下梯度都是相等的,这意味着即使对于小的损失值,其梯度也是大的。这不利于函数的收敛和模型的学习。
2.均方误差(Mean Square Error)指的就是模型预测值 f(x) 与样本真实值 y 之间距离平方的平均值。其公式如下所示:
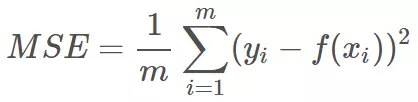
mse损失函数图像:?
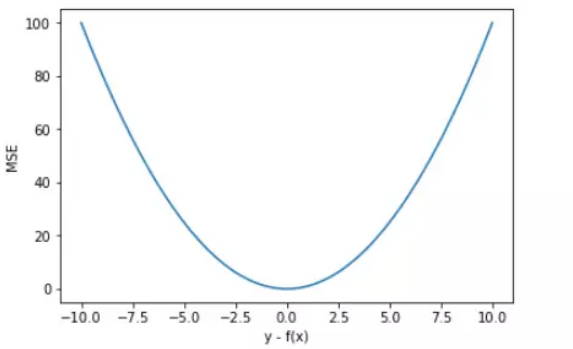
????????MSE 曲线的特点是光滑连续、可导,便于使用梯度下降算法,是比较常用的一种损失函数。而且,MSE 随着误差的减小,梯度也在减小,这有利于函数的收敛,即使固定学习因子,函数也能较快取得最小值。
????????平方误差有个特性,就是当?yi 与 f(xi) 的差值大于 1 时,会增大其误差;当?yi 与 f(xi) 的差值小于 1 时,会减小其误差。这是由平方的特性决定的。也就是说, MSE 会对误差较大(>1)的情况给予更大的惩罚,对误差较小(<1)的情况给予更小的惩罚。从训练的角度来看,模型会更加偏向于惩罚较大的点,赋予其更大的权重。
????????如果样本中存在离群点,MSE 会给离群点赋予更高的权重,但是却是以牺牲其他正常数据点的预测效果为代价,这最终会降低模型的整体性能。
????????值得一提的是,MAE 相比 MSE 有个优点就是 MAE 对离群点不那么敏感,更有包容性。因为 MAE 计算的是误差?y-f(x) 的绝对值,无论是?y-f(x)>1 还是?y-f(x)<1,没有平方项的作用,惩罚力度都是一样的,所占权重一样。针对 MSE 中的例子,我们来使用 MAE 进行求解,看下拟合直线有什么不同
# 结果评估
def evaluate_model(y_rec, y_all):
mae = []
mse = []
mape = []
for i in range(len(y_all)):
mae.append(abs(y_rec[i] - y_all[i]))
mse.append((y_rec[i] - y_all[i])**2)
mape.append(abs((y_rec[i] - y_all[i])/y_all[i]))
pass
print("拟合平均绝对误差(MAE)为:{:.4f}".format(np.mean(mae)))
print("拟合均方误差(MSE)为:{:.4f}".format(np.mean(mse)))
print("拟合平均绝对百分比误差(MAPE)为:{:.4f}%".format(100.0*np.mean(mape)))
evaluate_model(y_rec, y_test) 结果:

注意:这只是最简单的一种精确插值法,实际应用rbfn时可以有使用很少的资源却能达到很高的效率的效果。